 |
Zunächst definiert man einen zusätzlichen Basisvektor,
um der Symmetrie der hexagonalen Basisebene besser gerecht werden zu können. |
| |
Statt dieser EZ
mit drei Basisvektoren |
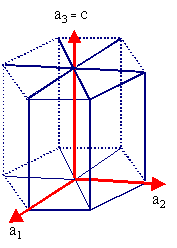 |
|
nimmt man eine EZ
mit vier Basisvektoren. |
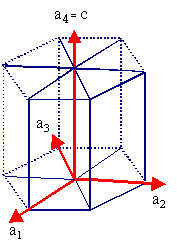 |
|
 |
Natürlich kann man nun die Indizes nicht mehr ganz unabhängig wählen. |
|
 |
Hat man im Dreier-System eine Richtung mit <UVW>
bestimmt, wird im Vierer-System dieselbe Richtung jetzt mit <uvtw> beschrieben.
|
|
 |
Die neuen "Vierer"-Indizes können aus den
alten "Dreier"-Indizes wie folgt berechnet werden: |
|
|
| u | = | 1/3 (2U – V) | | |
| | | v | = |
1/3 (2V – U) | | | |
| t | = | – (u + v) | | |
| | | w | = | W |
|
|
|
 |
Achtung! Bei t stehen absichtlich "kleine" Buchstaben. Diese Formeln kann
sich jeder selbst ableiten! Aber aufpassen! Im "Askeland"
hat sich z.B. bei diesen Formeln ein Fehler eingeschlichen. |
 |
Kristallographisch gleichwertige Richtungen haben mit der Viererindizierung dieselbe generelle
Indizierung, wie in einer Übungsaufgabe gezeigt wird. |
| |
 |
Für später (Einführung in die Materialwissenschaft II) gehen wir gleich noch
einen Schritt weiter und betrachten auch das sogenannte reziproke
Gitter |
|
 |
Hier muß man dazu nur wissen, dass das reziproke
Gitter aus dem realen Gitter abgeleitet wird, indem man Vektoren mit Komponenten h, k, l definiert, die senkrecht
auf den Ebenen {hkl} des realen Gitters stehen und eine Länge haben, die proportional zum Abstand dieser Ebenen
sind - und dass das reziproke Gitter für viele Zwecke wichtiger werden wird als das reale Gitter. |
 |
Ein reziprokes Gitter mit vier Komponenten der Basis- und
Translationsvektoren ist aber, wenn man genau hinschaut, grundsätzlich nicht definierbar; man bekommt unlösbare
Probleme sobald man die formale Definition bemüht. |
|
 |
Wir betrachten also zunächst das reziproke Gitter zu den drei
Basisvektoren a1, a2 und c des hexagonalen Gitters.
|
|
 |
Diese Basisvektoren des reziproken Gitters seien g1, g2
und g3. Sie ergeben sich für das hexagonale Gitter zu |
| |
|
 |
Ein so definierter reziproker Gittervektor steht per definitionem
senkrecht auf der Ebene mit den gleichen Dreier-Indizes. |
|
 |
Will man auch im reziproken Gitter die Vierer-Indizierung übernehmen, muß ein pseudoreziprokes
Gitter so eingeführt werden, daß
in ihm ein pseudoreziproker Gittervektor mit der Indizierung (hkil) senkrecht auf der Ebene (hkil) des Raumgitters
steht. |
|
 |
Da nun die Ebene (hkl) dieselbe ist wie die Ebene (hkil), besteht die Aufgabe darin, den
Vektor G = hg1 + kg2 + lg3 auszudrücken als
|
| |
| g | = |
hg'1 + kg'2 + ig'p
+ lg'3 |
|
|
|
 |
Wobei die gestrichenen Vektoren die Basisvektoren des pseudoreziproken
Gitters sind. Der Basisvektor g'p ist der vierte und eigentlich überflüssige Vektor. |
|
 |
Gleichzeitig gilt immer die Nebenbedingung h + k + i = 0. |
 |
Damit ist das pseudoreziproke Gitter definiert, es gilt |
| |
| gp' | = | 2
3a2 |
· a3 | = |
– (a1 + a2) |
|
|
 |
Das pseudoreziproke Gitter ist also mit dem realen Gitter
bis auf die Länge der Basisvektoren identisch. |
|
 |
Der große Vorteil des pseudoreziproken Gitter ist, daß sich in ihm Produkte von
Vektoren des realen und des reziproken Gitters besonders einfach ausrechnen lassen (eine Aufgabe, die häufig vorkommt). |
|
 |
Ist ein Translationsvektor des realen Gitters in der Viererindizierung gegeben durch r = <uvtw>
und ein Vektor des pseudoreziproken Gitters durch g = (hkil),
dann gilt für das Skalarprodukt
|
| |
| r · g | = | hu + kv + it + lw |
|
|
|
 |
d.h. man kann rechnen wie in einem cartesischen System. |
 |
Produkte zwischen Vierervektoren derselben Sorte sind etwas komplizierter, es gilt: Für |
| |
|
|
 |
ist das Skalarprodukt (mit der Abkürzung l = (2/3)(c/a)2): |
| |
| r1 · r2 | = |
3a2
2 |
· (u1 · u2 + v1 · v2 + t1· t2
+ l2 · w1 · w2) |
|
|
 |
Ähnlich im pseudoreziproken Gitter. Für |
|
|
|
|
 |
ist das Skalarprodukt |
| |
| g1 · g2 | = |
3a2
2 |
· (h1 · h2 + k1 · k2 + i1 · i2
+ l–2 · l1 · l2) |
|
|
© H. Föll (MaWi 1 Skript)


![]() 3.2.1 Richtungen und Ebenen im Gitter
3.2.1 Richtungen und Ebenen im Gitter ![]() Übung 3.2-1 Richtungen im Gitter
Übung 3.2-1 Richtungen im Gitter