3.3 Das reziproke Gitter

3.3.1 Formale Definition und Eigenschaften

Geometrische Konstruktion

	Wir benutzen zunächst die rein geometrische Definition der reziproken Gittervektoren um eine rein geometrische Konstruktion des reziproken Gitters durchzuführen. Die bereits gemachte Definition soll zunächst hier wiederholt werden.
	Ein reziproker Gittervektor Ghkl hat folgende Eigenschaften:
		1. Ghkl steht senkrecht auf der Ebenenschar {hkl}. 2. Die Länge von Ghkl ist proportional zum reziproken Abstand der Netzebenen, es gilt immer
		|Ghkl|  =  Ghkl =   2p dhkl
		Das läßt nur noch das Vorzeichen der Richtung offen; wir bräuchten dazu noch eine weitere Vereinbarung. Da aber die Richtung (d.h. wohin der Pfeil zeigt) reine Konventionssache und damit zunächst belanglos ist, schauen wir hier großzügig darüber hinweg bzw. lassen Ghkl und -Ghkl zu.
	Damit haben wir alles, um für ein beliebiges Raumgitter das zugehörige reziproke Gitter zu konstruieren; dies ist im folgenden gezeigt und erläutert.
		Raumgitter Reziprokes Gitter
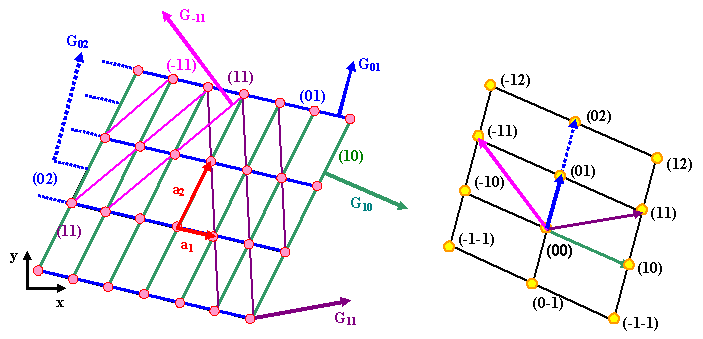
		Links ist das (zweidimensionale) Raumgitter gemalt - das sind die rosa Punkte . Weiterhin sind einige Ebenenscharen eingezeichnet; jede Schar hat eine eigene Farbe.
		Auf einer Ebene der Ebenenschar, die durch ihre Miller Indizes (hk) gegeben ist, wird der reziproke Gittervektor konstruiert und eingezeichnet. Die Länge dieses ersten reziproken Gittervektors können wir (noch) willkürlich wählen (damit legen wir die m– 1 Skala fest), die restlichen müssen sich an die dann definierte Skala halten.
		Wir wiederholen die Prozedur auf den restlichen Ebenen; damit bekommen wir einen Satz von Vektoren, den wir allgemein mit Gij bezeichnen. Alle Gij zeichnen wir jetzt von einem gemeinsamen Ursprung aus ein.
	Rechts im Bild ist das gemacht: Alle reziproken Gittervektoren sind von einem gemeinsamen Ursprung aus eingezeichnet. Ihr Endpunkte definieren zwangsläufig das reziproke Gitter.
		Für Puristen: Es ist natürlich in dieser Konstruktion nicht unmittelbar klar und bewiesen, daß der gewählte Satz von reziproken Gittervektoren ein Gitter aufspannt, in dem sich dann alle anderen möglichen reziproken Gittervektoren wiederfinden. Oder anders ausgedrückt: Dass alle reziproken Gittervektoren sich als Linearkombination von zwei "elementaren Basisvektoren" darstellen lassen.
		Schließlich würden die Endpunkte eines Satzes beliebiger Vektoren, von einem gemeinsamen Ursprung aus aufgetragen, nur einen beliebigen Punkthaufen definieren. Wenn man aber bedenkt, daß nach der Wahl zweier (niederindizierten) Ebenenscharen alle anderen Ebenenscharen festliegen, ist zumindest plausibel, dass das auch für die reziproken Gittervektoren gilt. Man kann das mit ein bißchen Geometrie leicht zeigen: nach der Wahl von G01 und G10 kann G11 nur noch als G11 = G01 + G10 dargestellt werden. usw.
	Das Bild verdeutlicht: Raumgitter und reziprokes Gitter sind in eindeutiger Weise korrelliert; hat man das eine, kann man das andere konstruieren.
		Außerdem wird die Indizierung der (gelben) Gitterpunkte des reziproken Gitters klar: Jeder Gitterpunkt symbolisiert eine Ebenenschar des Raumgitters.
		Damit bekommen wir eine erste Ahnung, warum das reziproke Gitter manche Dinge einfach macht: Alle niedrig indizierte Ebenen - und das sind in der Regel die wichtigen - finden sich in den ersten paar Gitterpunkten um den Ursprung wieder- was "weiter draußen" liegt, kann man oft schlicht vergessen.

	Formale Definition und Eigenschaften
	Formal definiert man das reziproke Gitter, indem man seine drei Basisvektoren gi; i = 1,2,3 angibt. Es gilt folgende Definition für drei Raumdimensionen:
		Wenn a1, a2, a3 die primitiven Translationsvektoren des Kristallgitters (= Raumgitter) sind, dann lassen sich die primitiven Translationsvektoren g 1, g2, g3 des reziproken Gitters nach folgender Vorschrift bestimmen:
		g1 =  2p · a2 × a3 a1 · (a2 × a3) =  2p · a2 × a3 V         g2 =  2p · a 3 × a1 a1 · (a2 × a3) =  2p · a3 × a1 V         g3 =  2p · a1 × a2 a1 · (a2 × a3) =  2p · a1 × a2 V
		Das Spatprodukt im Nenner gibt dabei das Volumen der Elementarzelle an. Damit ist auch die Richtung der reziproken Gittervektoren eindeutig definiert.
		Jetzt müssen wir natürlich zeigen, dass die geometrische und die formale Definition identisch sind. Das machen wir, indem wir systematisch die Eigenschaften der formalen Definition bestimmen.
	Formal definierte reziproke Gittervektoren haben folgende Eigenschaften (die wir in einer Übung beweisen):
	1. Jeder Punkt des reziproken Gitters kann durch einen Translationsvektor G des reziproken Gitters erreicht werden; G ist dabei wie üblich durch eine Linearkombination der Basisvektoren gi darstellbar. Sinnvollerweise machen wir das in dem Koordinatensystem, das durch die oben definierten gi aufgespannt wird. Damit gilt
		Gh,k,l = ( h · g1  +  k · g2  +  l · g3) h,k,l  =  ganze Zahlen  =   Miller Indizes der zu Gh,k,l gehörenden Ebenenschar
		Die h,k,l = ganze Zahlen sind dann die Miller Indizes der zu G gehörenden Ebenenschar (siehe Punkt 2.). Falls wir reziproke Gittervektoren in Komponenten darstellen, benutzen wir natürlich runde Klammern (hkl) für spezifische reziproke Gittervektoren und geschweifte Klammern {hkl} für alle kristallographisch gleichwertigen reziproke Gittervektoren. Auch lassen wir zukünftig den Index "h,k,l" am G eher weg um Schreibarbeit zu sparen.
		Wir werden natürlich niemals den Miller Index "k" mit dem Betrag des Wellenvektors k verwechseln!
		Weiterhin müssen wir uns bewußt sein, daß die gi nicht notwendigerweise ein cartesisches KO System aufspannen und daß ihre Länge im von ihnen aufgespannten KO System zwar per definition = "1" ist, nicht aber, wenn wir sie in cm–1 messen.
		Nehmen wir als einfachstes Beispiel ein kubisches Raumgitter mit |ai| = 1 cm. Das reziproke Gitter ist dann ebenfalls kubisch mit den Basisvektoren gi und |gi| = 2p cm–1. Translationsvektoren in beiden Gittern schreiben sich dann so
		Raumgitter Reziprokes Gitter Basissystem cm System Basissystem cm–1 System T = (u, v, w) T = (u, v, w) cm G = (h, k, l) G = 2p · (h, k, l) cm–1
		Während wir im (kubischen) Raumgitter also in beiden Systemen die formal gleiche Darstellung haben, gilt das nicht für das reziproke Gitter. Bildet man beispielsweise ein Skalarprodukt zwischen einem reziproken Gittervektor und einem Wellenvektor (der ja auch die Dimension cm–1 hat, d.h. im Raum des reziproken Gitters definiert ist, darf man den Faktor 2p nicht vergessen!
	2. Der reziproke Gittervektor G = (h,k,l) steht senkrecht auf der Netzebenenschar des Raumgitters mit den Miller-Indizes {h k l}.
		Die Richtung ist jetzt durch die formale Definition ebenfalls festgelegt, aber immer noch ziemlich uninteressant, da die Ebenen {hkl} und {–h–k–l} im Gitter identisch sind
		Das gilt übrigens nicht immer, falls wir reale Kristalle betrachten. Falls Vorzeichen so gewählt sind, dass z.B. auf der {111} Ebene von GaAs die Ga Atome liegen wenn man auf den Kristall "draufschaut", liegen auf der {-1, -1, -1} Ebene (der Rückseite des realen Kristalls) automatisch die As Atome. Die physikalischen Eigenschaften dieser "{111}" Kristalloberflächen können grundverschieden sein!
	3. Der Abstand dhkl zweier Ebenen der Netzebenenschar mit den Miller Indizes {h k l} ist
		dhkl  =  2p |Ghkl|
	4. Es gilt immer
		ai · gj  =  2 pdij
		Dabei ist dij = Kronecker Symbol, d.h.
		dij  =  { 1 für i = j 0 für i ¹ j
		Man kann das auch umdrehen und die erste Gleichung als Definition des reziproken Gitters betrachten. Sie hat den Vorteil dass sie nicht nur im Dreidimensionalen gilt, sondern für alle Dimensionen, z.B. auch für Kristalle in sechsdimensionalen Räumen. Wer das für abwegig hält, hat in MaWi I den diesbezüglichen Fortgeschrittenenmodul nicht angeschaut.
	5. Es gilt immer
		G · T   =   2 p · n           und damit             e i · G · T   =   ei · 2 p · n   =  1
		Mit n = ganze Zahl und T = beliebiger Translationsvektor des Raumgitters.
		Das ist, wie wir noch sehen werden, eine extrem wichtige Eigenschaft!
	Jetzt wird es aber Zeit, die Behauptungen 1. - 6. auch zu beweisen - in einer Übung:
		Übung 3.3-1 Eigenschaften des reziproken Gitters
	Eine letzte Eigenschaft, eigentlich die Haupteigenschaft die alles andere umfaßt, sei hier nur angedeutet:
	6. Das reziproke Gitter ist die Fouriertransformierte des Raumgitters. Mehr dazu findet sich im Link.
		Das bedeutet schlicht, daß jede im Kristall (jetzt nicht mehr nur im Gitter!) periodische Funktion (z.B. die Elektronendichte r(r) = r (r + T)) nach durch das reziproke Gitter vorgegebene "Ortsfrequenzen" Ghkl entwickelt werden kann.

	Was das bedeutet wollen wir uns verdeutlichen indem wir danach fragen, wie wir vom reziproken Gitter als Repräsentation des Raumgitters zum Kristall kommen:
		Wir haben bereits festgehalten, daß reziprokes Gitter und Raumgitter äquivalent sind; eines kann aus dem jeweils anderen in eindeutiger Weise konstruiert werden.
		Aber aus den Raumgitter kann ich einen Kristall machen - indem ich z.B. im einfachsten Fall auf jeden Gitterpunkt ein Atom setze.
	Es ist natürlich sinnlos, auf einen reziproken Gitterpunkt ein Atom zu setzen. Der dann erhaltene Kristall ist halt irgendein Kristall, er hat aber mit dem zum betrachteten Raumgitter gehörenden Kristall nichts zu tun.
		Stattdessen setze ich auf jeden reziproken Gitterpunkt die zugehörige Fourierkomponente der betrachteten Kristalleigenschaft . Ein "Atom" ist z.B durch die lokale Elektronendichte r (r) für viele Zwecke hinreichend definiert.
	In Formeln sieht die Fourierentwicklung von z.B. der Ladungsdichte r(r) nach Komponenten bei reziproken Gitterpunkten G so aus
		r(r)  =  G S G nG · exp (i · G · r)
		Die Fourierkoeffizienten nG erhält man aus
		nG  =   1 V  · ó õ V r(r) · exp – (i · G · r) · dV
	Das Bild unten zeigt schematisch, was das für ein einfaches Beispiel bedeutet
		Wir haben in irgendeine beliebige Richtung x eine periodische Funktion für die Elektronendichte r(x). In eine andere Richtung sieht r anders aus, ist aber immer periodisch.
		Die Fourierentwicklung produziert für jeden reziproken Gitterpunkt eine Fourierkomponente nG, deren Wert durch die Größe der blauen Kreise angedeutet ist.
	Das reziproke Gitter plus die Fourierkomponenten der im Raumgitter + Basis = Kristall betrachteten (und im Raumgitter periodischen) Eigenschaft enthält jetzt exakt dieselbe Information wie eine komplette Darstellung des Kristalls - aber oftmals in viel kompakterer und eleganterer Form.
		Wie im Bild schon angedeutet, werden die Fourierkomponenten rasch klein für große G-Vektoren, d.h. für nicht "niedrig-indizierte Ebenen". Es reicht also für viele Zwecke, nur einen kleinen Ausschnitt aus dem reziproken Gitter zu betrachten um genügend genau rechnen zu können.
	Aber das gilt alles nur für periodische Eigenschaften. Für nichtperiodische Eigenheiten eines Gitters - zum Beispiel für seine Gitterdefekte - ist das reziproke Gitter ziemlich witzlos.
	Zum Schluss noch eine verhältnismäßig einfache, aber gehaltvolle Übung:
		Übung 3.3-2 Das reziproke Gitter der einfachen Bravaisgitter
		Fragebogen / Questionaire Multiple Choice Fragen zu 3.3.1

© H. Föll (MaWi 2 Skript)