3. Struktur von Kristallen

	3.1 Grundbegriffe
	3.1.1 Wiederholung
	In diesem sehr kurzen Unterkapitel werden nur die wichtigsten Dinge aufgezählt (und verlinkt), die wir über Kristalle bereits gelernt haben.
	Betrachten wir zunächst den Idealkristall
		Ein Idealkristall definiert sich über
		Kristall = Gitter + Basis = + oder
	Das Gitter ist ein mathematisches Konstrukt; eine sinnvolle Klassifizierung nach Symmetrien benutzt die 14 Bravais Gitter
		Jeder Vektor T des Gitters läßt sich durch eine geeignete Kombination der im Ortsraum definierten Basisvektoren ai darstellen:
		T = n1 · a1  +  n2 · a2  +  n3 · a3
		Dabei sind die ni ganze Zahlen (inkl. der Null). Ein so definierter Vektor T endet immer auf einem Gitterpunkt und heißt auch Translationsvektor des Gitters weil eine Verschiebung des Gitters um T das ideale, d.h. ¥ ausgedehnte Gitter unverändert läßt.
	Man muß aber zur Beschreibung eines Kristalls nicht unbedingt eine auf Bravaisgitter oder primitiven Gittern beruhende Elementarzelle nehmen, es gibt auch noch eine andere Optionen: Die Wigner-Seitz Elementarzelle wird hier wichtig werden; wir schauen sie mal kurz an.
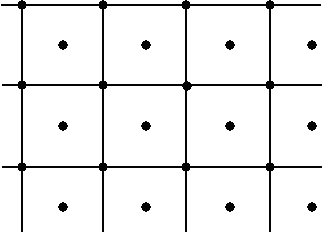
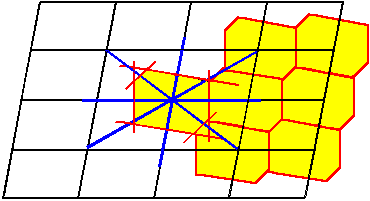
		Gegeben sei ein beliebiges Gitter (schwarz; hier zweidimensional). Von einem willkürlichen Gitterpunkt aus ziehen wir Strecken zu benachbarten Gitterpunkten (blau), auf denen wir Mittelhalbierende errichten (rot). Die Mittelhalbierenden bilden einen geschlossenen Polygonzug sobald wir genügend viele Strecken konstruiert haben.
		Im Dreidimensionalen resultiert ein Polyeder - die Wigner-Seitz Elementarzelle. Das resultierende (etwas unelegante) Gitter ist zur Konstruktion eines Kristalls genau so gut geeignet wie das ursprüngliche Gitter, wir müssen nur vereinbaren, dass wir die Basis in das Zentrum der Wigner-Seitz Zelle setzen.
		Die Konstruktion mag die vorhandenen Symmetrien verbergen und unelegant erscheinen - aber sie ist universell und wird sich als nützlich erweisen.
	Die Basis beschreibt die Konfiguration der Atome; d.h. ihre Art, Zahl und Anordnung im Raum.
		Eine Basis kann sehr einfach sein, z.B ein Atom der Sorte i auf den Koordinaten (0 0 0) eines cartesischen KO-Systems.
		Sie kann aber auch sehr kompliziert sein und viele Atome verschiedener Sorten umfassen. Wir haben dann j Sätze von Vektoren ri die zu den Atomen einer Atomsorten i führen; und soviel Sätze j wie Atomsorten.
	Im Gegensatz zum Idealkristall besteht ein Realkristall meist aus sehr vielen kleinen Kristalliten, die wiederum Gitterdefekte enthalten. Grob klassifiziert unterscheiden wir vier Defekttypen:
		0-dimensionale Defekte; z.B Atomare Fehlstellen.
		1-dimensionale Defekte; das sind die Versetzungen.
		2-dimensionale Defekte; z.B. Korngrenzen oder Phasengrenzen.
		3-dimensionale Defekte; z.B. Ausscheidungen.
	Beschreibung von Richtungen und Ebenen in Kristallen:
		Grundsätzlich wird im Koordinatensystem des durch die Basisvektoren definierten Gitters gearbeitet. In nicht-kubischen Kristallen (d.h. nicht-cartesischen Systemen) ist dann bei den vertrauten Formeln der Vektorrechung Vorsicht geboten!
	Grundsätzlich werden für die Beschreibung von Richtungen und Ebenen die Miller-Indizes verwendet. Die Beschreibung bezieht sich immer auf das Gitter. Die Zentren einzelner Atome müssen deshalb nicht auf Richtungen oder Ebenen liegen.
		Die Konvention für die Richtungs- und Ebenenindizierung ist:
		<u v w> = Gesamtheit der kristallographisch gleichwertigen Richtungen. [u v w] = Spezifische Richtung. {h k l} = Gesamtheit der kristallographisch gleichwertigen Netzebenenscharen. (h k l) = Spezifische Netzebenenschar.
		Fragebogen / Questionaire Multiple Choice Fragen zu 3.1.1

© H. Föll (MaWi 2 Skript)