 |
Grundsätzlich interessieren wir uns jetzt für das Verhalten von Wellen in Kristallen, wobei nur Wellen interessieren, deren Wellenlängen l
= 2p/|k| nicht sehr viel größer sind als die Gitterkonstante a
des Kristalls. Wir gewöhnen uns schon mal daran, dass wir anstelle der Wellenlänge l
zunehmend den Wellenvektor k der betrachteten Welle verwenden. |
|
 |
Damit reden wir nicht über "Licht" mit Wellenlängen im 1
µm Bereich; auch nicht über ultraviolettes Licht mit Wellenlängen im 0,x µm Bereich, wohl
aber über Röntgenstrahlung und "Materiewellen". |
|
 |
Warum diese Einschränkung? Weil Wellen mit zu kleinen Wellenvektoren
(und damit zu großen Wellenlängen) die Periodizität des Kristalls gar nicht spüren können (wir werden noch sehen warum). Für diese Wellen ist der Kristall schlicht ein
homogenes Medium; für Lichtwellen z.B. hinreichend charakterisiert durch den Brechungsindex n = (er)½ oder die (relative) Dielektrizitätskonstant er. (Elementarformeln wie diese werden übrigens nicht mehr erklärt!) |
 |
Wir haben schon viel über Elektronenwellen gelernt, die als Lösung der
Schrödingergleichung (für das Modell des freien Elektronengases) im Kristall herumlaufen.
|
|
 |
Jetzt fragen wir uns, was geschieht, wenn wir Elektronen(wellen) von außen
in den Kristall "hineinschießen". |
|
 |
Die Antwort auf diese Frage wurde zuerst theoretisch gegeben, heute ist sie in jedem (Durchstrahlungs)elektronenmikroskop (transmission electron microscope, TEM)
experimentell implementiert. |
 |
Schauen wir uns das Prinzip des TEM ein bißchen genauer an. (im Link
gibt es zusätzliche Details). |
|
 |
In einer "Elektronenkanone" wird ein halbwegs
gebündelter Elektronenstrahl erzeugt. Dazu werden durch Glühemission
aus einer Kathode Elektronen freigesetzt und elektrostatisch durch eine positiv geladenen Anode beschleunigt. Mit "Wehnelt
Zylindern" oder anderen elektrostatischen oder magnetischen "Linsen" wird der erzeugte Elektronenstrahl gebündelt
und fokussiert. |
|
 |
Das generelle Prinzip wird auch in jeder Fernseh- oder Monitor-Bildröhre genutzt - entscheidend
für die Wellenlänge der Elektronenstrahlwelle ist die Höhe der Beschleunigungsspannung Ue;
sie bestimmt Energie Ee, Impuls pe, und damit auch die Wellenlänge
le des Elektronenstrahls |
|
 |
Die Energie Ee ist natürlich schlicht |
| |
|
|
 |
d.h. die Elektronen im Elektronenstrahl haben genau (± thermisches Rauschen im
1 eV Bereich) die Energie in [eV] die der Beschleunigungsspannung entspricht - so war die Energieeinheit [eV]
schließlich definiert. |
 |
Diesen Elektronenstrahl jagen wir durch die
Probe hindurch (sie muß dann natürlich sehr dünn sein; siehe unten). |
|
 |
Die Wechselwirkung des Elektronenwellenstrahls mit der Struktur der Probe (inklusive der Defekte
in dieser Struktur) führt zu einer Modulation der Intensität (oder besser Amplitudenquadrat) des austretenden
Strahls an der Unterseite der Probe. |
|
 |
Die Intensitätsverteilung wird mit einem elektronenoptischen System stark vergrößert
auf den Bildschirm projeziert - voilà, das Bild der Struktur! |
 |
Die Wellenlänge erhalten wir sofort über die de Broglie Beziehung und über die Beziehung zwischen Energie und Wellenvektor, die wir vom freien Elektronengas
kennen, und die wir hier mit mehr Berechtigung anwenden dürfen als in einem Kristall. |
| |
| pe = |
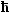 · k · k | = |
2p
le |
| Ee = |
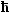 2 · k2 2 · k2
2me |
= | e ·Ue |
|
|
 |
Als Ergebnis erhalten wir die schlichte (aber auch nicht-relativistische!) Formel |
| |
|
 |
Damit sind Zahlenwerte leicht zu errechnen: |
| |
| Ue [V] |
le [nm]
| | 10 |
0.388 |
| 1 000 | 0.0388
| | 10 000 |
0.0123 |
|
 |
Gebräuchliche Elektronenstrahlsysteme
verwenden typische Spannungsbereiche wie folgt: |
|
|
| Cathode Ray Tube (Bildröhre) |
CRT |
U » 20 kV |
| RasterElektronenMikroskop |
REM |
U = (1 - 20) kV |
| TransmissionsElektronenMikroskop |
TEM | U = (100 - 400) kV |
"High Voltage" TransmissionsElektronenMikroskop
(diese
Mikroskope sind immer als TEM aufgebaut) |
HVTEM | U
» (1 - 3) MV |
|
|
 |
Für übliche Spannungen sind die Wellenlängen damit immer deutlich kleiner als
die Gitterkonstanten. |
 |
Neben den Elektronen können zur Strukturanalyse auch Neutronen, Photonen (d.h. also Röntgenstrahlung) und Atome eingesetzt werden.
|
|
 |
Die Wellenlängen ergeben sich nach der Formel von oben; wir müssen nur die jeweilige
Masse und statt e ·Ue die jeweilige Teilchenenergie einsetzen. Für Neutronen und Atome
erwarten wir aufgrund der sehr viel höheren Masse (ungefähr Faktor 2 000) eine entsprechend kleinere Wellenlänge. |
 |
Soweit es die Welleneigenschaften der Teilchen betrifft, sind zunächst alle
Teilchen "gleich" - wir haben immer für die (Momentaufnahme) jeder ebenen
Welle immer die Formel |
|
|
|
 |
Neben der in k "versteckten" Wellenlänge,
unterscheiden sich die diversen Teilchenwellen aber grundsätzlich in der Art ihrer
Wechselwirkung mit Materie. Und zwar insbesondere in einer Art von Wechselwirkung die uns hier weniger interessiert, nämlich
in der Absorption. Wir haben folgendes Verhalten: |
|
 |
Röntgenstrahlung durchdringt auch dickere Proben
(z.B. Ihren Körper); einige mm sind immer drin. Schwere Atome absorbieren stärker als leichte, und energiereiche
Strahlung kommt weiter. Röntgenanlagen sind relativ billig, so um € 100.000. Fast jeder Arzt hat eine Röntgenanlage,
und jedes materialwissenschaftliche Institut hat mehrere. |
|
 |
Neutronenstrahlen; üblicherweise aus einem Kernreakor
"abgezapft", können sehr durchdringend sein, wiederum sind leichte Elemente tendenziell weniger absorbierend.
Allerdings können hier kernphysikalische Spezialphänomene zuschlagen - bestimmte Isotope
können sehr stark absorbierend wirken (das ist z.B wichtig für die Steuerung eines Kernreaktors). In manchen Fällen
kann man viele cm eines Materials durchstrahlen. Neutronenstrahlen sind naturgemäß extrem teuer; in Deutschland
gibt es < 6 Einrichtungen an denen "Neutronenstreuung" möglich ist. |
|
 |
Elektronenstrahlen werden in allen Materialien sehr stark
absorbiert, sie kommen nicht weit - Größenordnung µm. Die Präparate für TEM müssen
dementsprechend sehr dünn sein - einige µm für HVTEM und ca. 10 nm für höchste
Auflösung. |
 |
Die Wechselwirkung von Welle und Materie bietet 3 grundsätzlich verschiedene
Arten von Informationsbeschaffung über das Material: |
|
 |
1. Messung der lokalen Dicke/Materiedichte über
die Absorption. Das macht der Arzt in der Schattenprojektion des Körpers mit Röntgenstrahlen - nicht weiter spannend. |
|
 |
2.
Strukturbestimmung mittels Beugungsphänomenen. Das entscheidende Stichwort ist
Interferenz - zwischen Welle und periodischem Objekt. Dies ist
die eigentliche Domäne der Strukturbestimmung mit Wellen. |
|
 |
3. Direkte Strukturabbildung. Das ist die Domäne
der Elektronenmikroskopie, in der man ein Bild der Struktur enthält. Hinter dem "Bild" steckt aber wiederum
die Beugung der Wellen. |
 |
Die im folgenden abgeleiteten Beziehungen zur Strukturbestimmung vernachlässigen
die Absorption und gelten für alle Wellen; sie sind jedoch insbesondere nützlich
für Elektronen- und Röntgenstrahlen. |
|
|
© H. Föll (MaWi 2 Skript)