3.2.2 Das Bragg-Gesetz

Vorbemerkungen

	Wellen sind Wellen sind Wellen sind Wellen sind... . Das klassische Youngsche Experiment mit Lichtwellen und Schlitzen in einer Blende gilt für jede Welle.
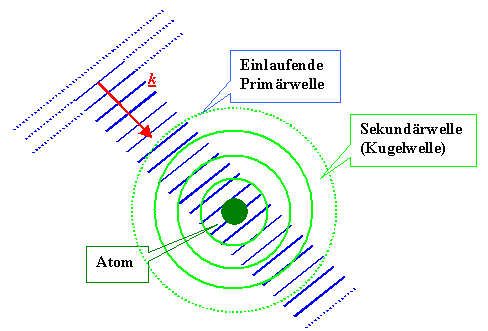
		Am jedem Schlitz (Kratzer im Glas, Hindernis, Atom, ...) werden von der einfallenden ebenen Welle Kugelwellen angeregt. Dabei soll in einer ersten Näherung nur ganz wenig Energie in die Kugelwellen fließen - die einfallende Welle wird also nicht nennenswert geschwächt.
		Wir wissen aber aus der "allgemeinen menschlichen Erfahrung" (die das Finanzamt immer gerne zitiert), daß ein einziges Atom einen Röntgen- oder Elektronenstahl auch nicht merklich beeinflussen kann; so ganz schlecht wird die Näherung also nicht sein.
		Die von vielen Atomen erzeugten Kugelwellen interferieren miteinander; das Ergebnis der Interferenz produziert irgendwelche neuen Wellen die neben der einfallenden (und in dieser Näherung ungeschwächt weiterlaufenden) Welle jetzt zusätzlich beobachtet werden können.
		Im klassischen Experiment mit 2 Spalten sieht das so aus
		Die von den zwei "Schlitzen" ausgesandten Sekundärwellen (= Halbkugelwellen) verstärken sich durch konstruktive Interferenz in bestimmten Richtungen, in anderen Richtungen hingegen löschen sie sich gegenseitig aus. Nehmen wir viele Spalten oder "Kratzer" auf einem Glasstück, die in konstanten Abständen angeordnet sind, erhalten wir ein (zweidimensionales) optisches Gitter. Sekundärstrahlung wird für eine gegebene Wellenlänge nur noch in wenigen ganz bestimmten Richtungen auftreten; wir erhalten "Reflexe".
	Hochenergetische Elektronen, die als dünner (Primär)strahl von außen in einen Kristall geschossen werden, verhalten sich im Kristall genauso wie außerhalb - nämlich als Wellen. Da ihre Wellenlänge zu den Dimensionen der Atome "paßt", regen sie diese zur Aussendung von Kugelwellen an.
		Die von den Atomen ausgesandten Kugelwellen verstärken sich durch konstruktive Interferenz in bestimmten Richtungen, in anderen Richtungen hingegen löschen sie sich gegenseitig aus. Alles wie oben - nur daß wir jetzt dreidimensional sind.
		Experimentell finden wir, daß nur in einige wenige Richtungen Sekundärstrahlen auftreten, d.h. Elektronenstrahlen den Kristall verlassen. Es erscheint als ob der Primärstrahl in bestimmte Richtungen reflektiert wird, auf einem Bildschirm um den Kristall herum erscheinen einige scharfe Reflexe.
		Diese in Richtungen der Beugungsmaxima gefundenen Reflexe werden auch als Bragg-Reflexe bezeichnet. Sie lassen sich z.B. mit Hilfe eines Leuchtschirms nachweisen.
		Die Beugung von Wellen am Kristallgitter wurde 1912 erstmals von Max von Laue nachgewiesen (allerdings für Röntgenstrahlung).

Herleitung der Bragg Bedingung

	Zunächst machen wir uns klar, was wir ableiten wollen: Wir lassen eine ebene Welle unter irgendeinem Winkel Q auf einen Kristall fallen.
		Nach dem bereits Gesagten müssen wir erwarten, daß sie einerseits einfach durch den Kristall läuft, andererseits aber auch vielleicht an Netzebenen des Kristall reflektiert wird, dabei gilt dann Einfallswinkel = Ausfallswinkel
		Diese Situation ist unten mal vereinfacht gezeigt; die betrachtete Netzebenenschar des Kristalls wirkt in diesem Bild auf die einfallende Welle wie ein Spiegel auf Licht. Im Grunde brauchen wir für die prinzipielle Betrachtung gar keine Atome, aber man darf sich getrost auf jedem Gitterpunkt mal ein Atom vorstellen.
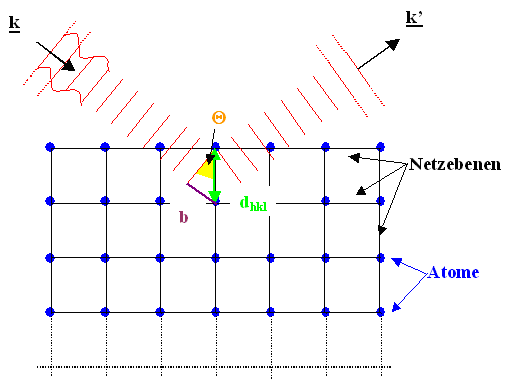		Bragg Bedingung erfüllt: Reflektion
		Die einfallende Welle hat den Wellenvektor k, die reflektierte Welle den Wellenvektor k'. Der Netzebenenabstand ist dhkl; wir können ihn leicht aus den Miller Indizes berechnen; b ist der Gangunterschied zwischen zwei Netzebenen.
		Die roten Linien markieren die Wellenfront in dem hier interessanten Bereich; im Prinzip sind sie natürlich genau wie die Netzebenen ¥ ausgedehnt (strichliniert angedeutet).
	Im Gegensatz zu normalem Licht und einem normalen Spiegel wird jedoch nicht jede Welle reflektiert, sondern nur Wellen die einen ganz bestimmten Einfallswinkel Q = QBragg = QB haben oder, wie man auch sagt, bezüglich des Winkels eine sigenannte "Bragg.Bedingung" erfüllen. Warum das so ist, machen wir uns sofort klar.
		Vorher nochmal das Bild von oben; nur der Einfallswinkel Q wurde leicht geändert - die Bragg Bedingung sei jetzt nicht mehr erfüllt
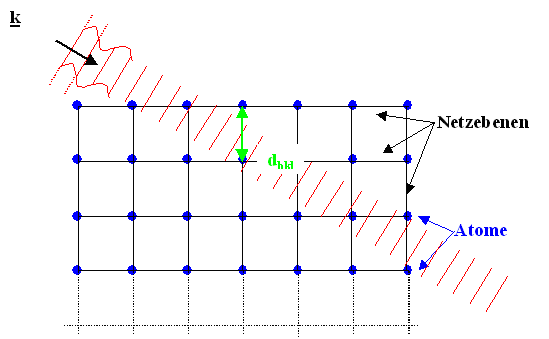		Bragg Bedingung nicht erfüllt: Durchgang
	Das Bragg-Gesetzes oder die Bragg-Beziehung, die wir herleiten möchten, muß uns also sagen für welche speziellen Winkel Reflektion erfolgt und was diese Bragg-Winkel bestimmt.
		Die Herleitung des Bragg-Gesetzes ist verhältnismäßig einfach; insbesondere genügt es, nur zwei Netzebenen aus der ganzen Netzebenenschar zu betrachten. Wir nehmen die eingezeichneten horizontalen Netzebenen um das Bildchen einfach zu halten, wir könnten aber jede beliebige Netzebenenschar nehmen und was wir herleiten gilt auch für jede beliebige Netzebenenschar {hkl}.
		Betrachten wir die reflektierte Welle mit Wellenvektor k', so sehen wir, daß konstruktive Interferenz dann und nur dann auftreten wird, wenn der Gangunterschied 2b zwischen den an zwei benachbarten Netzebenen reflektierten Wellen genau ein Vielfaches der Wellenlänge l beträgt.
		Das war's schon. Wir müssen die obige Prosa nur noch als Formel hinschreiben:
		2 · b  =  n · l    n = 1, 2, 3,..           b  =  dhkl · sinQ
		Damit ergibt sich für den spezifischen Winkel QB bei dem, und nur bei dem Reflektion stattfindet die gesuchte Bragg-Beziehung
		2 · dhkl · sinQB  =   n · l sinQB = n · l 2 · dhkl
	Eine simple, aber bemerkenswerte Gleichung!
	Zunächst fällt auf, daß für n · l > 2 · dhkl  keine Lösungen existieren, d.h. für Wellenlängen die größer sind als 2 mal die Gitterkonstante a gibt es schlicht keine Möglichkeit der konstruktiven Interferenz an Kristallen (denn das größtmögliche dhkl = a haben wir für die {100} Ebene).
		Für sehr kleine l liegen die möglichen Reflexe sehr dicht beisammen; damit verwischt sich der Effekt der Beugung.
	Dann haben wir immer eine ganze Reihe von passenden Winkeln, oder Ordnungen von Reflexen, je nachdem welche ganze Zahl n wir wählen. Das ist ein bißchen störend, denn hier scheint ein Stück Unbestimmtheit vorzuliegen: Eine Ebenenschar macht viele Reflexe - wie soll man dann von den Reflexen auf die Ebene zurückschließen?
		Ist aber kein Problem. Denn für n = 1,2,3,... können wir auch schreiben dhkl, ½dhkl, (1/3)dhkl usw. Alles was wir jetzt tun müssen, ist die Reflektion 2. Ordnung (d.h. n = 2) nicht der Ebenenschar {hkl} zuzuschreiben, sondern der Schar {2h 2k 2l}, die Reflektion 3. Ordnung (d.h. n = 3) der Schar {3h 3k 3l} usw.; die Abstände stimmen dann automatisch.
		Auch deswegen wurde bei der Einführung der Miller Indizes das "Kürzen" nicht erlaubt, d.h. wir unterscheiden zwischen der {111}-Ebene und der {222}-Ebene usw.
	Schließlich bemerken wir noch, daß die Bragg-Bedingung für jede denkbare Ebenenschar gilt. Reflexe könne also - wir sind dreidimensional - in alle möglichen Richtungen auftreten, auch nach unten, durch den Kristall hindurch - immer vorausgesetzt, daß für die betrachtete Ebenenschar die Bragg-Bedingung erfüllt ist. Ist sie nicht erfüllt, passiert schlicht nichts.
		Im Umkehrschluß stellen wir fest, daß experimentell ermittelte Reflexe Aussagen über die Abstände von Ebenen enthalten und damit, wenn auch etwas indirekt, Aussagen über das Gitter. Mit geeigneten Beugungsexperimenten können wir also bestimmen, was für ein Bravaisgitter mit welcher Gitterkonstante vorliegt - wir haben das Universalinstrument der Strukturanalyse gefunden!
		Das Beugungsbild definiert als Endpunkte der erlaubten k'-Vektoren besteht also ggf. aus Punkten im Raum.
	Es ist noch wichtig festzuhalten, was uns die Bragg- Bedingung nicht sagt: Kein Wort über die Intensität der Reflexe!
		Aus der Bragg-Bedingung folgt bei Kenntnis der Geometrie lediglich, in welchen Raumrichtungen wir Reflexe erwarten dürfen, aber keinesfalls wie intensiv diese Reflexe sein werden.
		Und das ist auch gut so! Denn bisher haben wir nur mit dem Gitter des Kristalls gearbeitet; Atome waren formal gar nicht nötig. In realen Beugungsexperimenten erwarten wir aber schon, daß sich die Ergebnisse trotz gleichem Gitter unterscheiden werden, falls wir verschiedene Kristalle, d.h. verschiedene Basen und damit verschiedenen Atome haben. Und das Unterscheidungsmerkmal kann dann nur noch in den Intensitäten der Reflexe liegen!
	Bevor wir jetzt aber weitermachen mit der Diskussion der Konsequenzen der Bragg-Bedingung, wollen wir sie erst auf eine viel elegantere und mächtigere Form bringen. Dazu müssen wir eine neue Beschreibungsart von Gittern kennenlernen, das sogenannte reziproke Gitter, das sich zum Raumgitter etwa so verhält wie das Frequenzspektrum eines periodischen Signals zu der Darstellung über die Zeit.
		Wir werden das reziproke Gitter erst anschaulich, und danach mathematisch-formal einführen.

Bragg Bedingung in Vektorschreibweise

	Das Bragg-Gesetz in obiger Formulierung ist eine Skalargleichung, in der statt dem Wellenvektor die skalare Wellenlänge steht. Eine Vektorgleichung wäre automatisch sehr viel allgemeiner und mächtiger; wir wollen deshalb jetzt das Bragg-Gesetz auf Wellenvektoren umschreiben. Das machen wir zunächst etwas unmathematisch durch eine Plausibilitätsbetrachtung.
		Dazu betrachten wir nochmals das Prinzipbild oben und unten. Wir haben eine einfallende Welle, vollständig charakterisiert durch ihren Wellenvektor k (und noch die hier uninteressante Amplitude), und eine gebeugte Welle k'. Da wir nur elastische Streuung betrachten, d.h. keine Energieänderungen zulassen, gilt immer
		|k|  =  |k'|
		Eine Vektorbeziehung zwischen k und k' kann im einfachsten Fall dann nur so aussehen
		k  –  k'  =  G       |k|  =  |k'|
		Dabei ist G ein zunächst noch undefinierter Vektor, in dem aber "irgendwie" das Gitter stecken muß. Da die Wellenvektoren aber nicht im "normalen" Raum definiert sind, sondern im "Zustandsraum", muß auch G ein Vektor in diesem Raum sein.
	Falls wir zeigen können, daß ein Vektor G immer so definiert werden kann, daß unter allen Umständen für eine gegebene Geometrie (inkl. Gitter) die skalare Bragg Bedingung erfüllt ist, haben wir die gesuchte Vektorformulierung gefunden.
		Das ist einfach. Wir müssen nur die obige Vektorgleichung in Komponenten hinschreiben (das Bild unten hilft dabei), um sofort zu sehen, wie sich G bestimmt. Wir haben (zweidimensional)
		æ è kx kz ö ø – æ è k'x k'z ö ø = æ è Gx Gz ö ø = æ è 0 Gz ö ø = æ è 0 k · sinQ + k · sinQ ö ø = æ è 0 2k · sinQ ö ø
		da in der gewählten Geometrie offensichtlich k'z = –kz gilt.
	Das schauen wir uns nochmal genau an:
	Für sinQ haben wir in der bereits abgeleiteten skalaren Bragg-Beziehung schon eine Formel gefunden, die wir verwenden können.
		Ersetzen wir noch die Wellenlänge l durch l = 2p/|k| = 2p/k, erhalten wir für die z-Komponente des Vektors G
		Gz =  2k · sinQ  =  2k · l 2 · dhkl   =  k · 2p k · dhkl = 2p dhkl
		Die z-Komponente des Vektors G ist aber identisch mit dem Vektor G selbst, da G offenbar immer senkrecht auf der betrachteten Ebene {hkl} stehen muß.
	Damit haben wir unseren Ansatz gerechtfertigt, das Ergebnis (das wir gleich dreidimensional verallgemeinern) ist erstaunlich einfach; wir schreiben es nochmals auf:
		Die Bragg-Bedingung in vektorieller Form lautet
		k – k'  =  Ghkl |k|  =  |k'|
	In Worten bedeutet das:
		Ein beliebiger Wellenvektor k wird an der Ebenenschar {hkl} dann und nur dann gebeugt, falls die Differenz von einfallendem und reflektiertem Wellenvektor identisch ist zu einem Vektor Ghkl, der die Ebenenschar {hkl} symbolisiert. Dabei hat Ghkl zwei einfache Eigenschaften, die diesen Vektor aber eindeutig bestimmen:
		1. Ghkl steht senkrecht auf der Ebenenschar {hkl}.
		2. Die Länge von Ghkl ist proportional zum reziproken Abstand der Netzebenen, es gilt immer
		|Ghkl| = 2p dhkl
	Wer bei dieser "Herleitung" das mathematische Bauchweh bekommt, schaut sich den Link an. Unabhängig davon muss aber noch eine Anmerkung gemacht werden: Der Abstand zwischen den Ebenen dhkl einer Ebenenschar definiert nur den Betrag von G. Die Richtung haben wir, wenn man das genau betrachtet, völlig willkürlich gewählt. Das bedeutet, dass wir im Bild oben bei G die Richtung auch undrehen könnten. Dann lautet die Bragg Bedingung: k' – k  =  Ghkl. Sobald wir eine formale Definition von G haben, sind die Vorzeichen dann festgelegt.

Das reziproke Gitter

	Wir haben mit der vektoriellen Formulierung der Bragg-Bedingung einen außerordentlich weitreichenden Schritt gemacht.
		Wir haben Netzebenenscharen durch Vektoren repräsentiert. Nehmen wir nun alle möglichen Netzebenen eines gegebenen Gitters, konstruieren die jeweiligen Vektoren Ghkl, und tragen all diese Vektoren von einem gemeinsamen Ursprung an auf, werden die Endpunkte aller Vektoren ebenfalls ein Gitter definieren.
		Dieses Gitter nennen wir das reziproke Gitter, die Vektoren G heißen reziproke Gittervektoren. Ihre Einheit ist [G] = m– 1.
		Denn da alle Netzebenen eines Gitters durch die Angabe von drei Basisvektoren eindeutig definiert sind, werden auch drei Basisvektoren im reziproken Gitter ausreichen (müssen), um alle Vektoren des reziproken Gitters darstellen zu können.
	Das reziproke Gitter läßt sich in eineindeutiger Weise aus den Raumgitter konstruieren; die Umkehrung gilt auch. Das reziproke Gitter ist damit vollkommen äquivalent zum Raumgitter, d.h. es enthält exakt dieselbe Information wie das Raumgitter.
		Es ist aber für alle Phänome die sich mit Wellen in Kristallen befassen ungleich wichtiger als das Raumgitter, da sich die Mathematik sehr viel einfacher gestaltet (oder überhaupt nur im reziproken Gitter durchziehen läßt).
		Wir werden uns deshalb im nächsten Unterkapitel ausführlich mit dem reziproken Gitter befassen.
		Fragebogen / Questionaire Multiple Choice Fragen zu 3.2.2

© H. Föll (MaWi 2 Skript)