|
Im vorherigen Unterkapitel haben wir die möglichen Zustände
des Elektrons und die möglichen Energien des Elektrons bestimmt. Im folgenden
werden wir uns der Frage widmen, wieviele Zustände es zu einer Energie gibt und
zeigen, daß diese Anzahl der Zustände für verschiedene Energien unterschiedlich ist. |
|
 |
Die Anzahl der Elektronenzustände pro Energie(intervall) und
pro Volumeneinheit wird als Zustandsdichte bezeichnet. Zustandsdichten sind
fundamentale Bestimmungsgrößen von Systemen wie z.B Kristalle, amorphe Körper, Hohlraumresonatoren für
Schallwellen oder Lichtwellen, usw. |
|
 |
Nochmal. weil's so wichtig ist: Die hier angesprochen Zustandsdichte ist
ein reale Eigenschaft realer Materialien und Systeme, und nicht nur eine mathematische Definition in einem skurrilen Modell
eines Kristalls. Sie inkorporiert die zentralen elektronschen Eigenschaften des Materials; ihre reale Wichtigkeit kann kaum
überschätzt werden. Hier rechnen wir halt so gut wir können, wenn's nicht gut genug sein sollte, werden wir
Zustandsdichten, wie immer, einfach messen! |
|
 |
Für unser Modell des freien Elektronengases
können wir die Zustandsdichte im Prinzip durch abzählen erhalten. |
 |
Versuchen wir es mal. Gleichzeitig tabellieren wir, wieviele Elektronen in den
Zuständen, die zu einer Energie gehören, Platz haben. (wobei wir immer daran denken, daß wegen des Pauli-Prinzips ein Zustand mit maximal
zwei Elektronen ("Spin up" und "Spin down")
besetzt werden kann. |
| |
| Quantenzustand |
Energie
(× Konstante ) |
Zustände |
Zahl der e–
pro E
| | nx |
ny |
nz |
| 0 | 0 | 0 |
0 |
|
1 | 2 |
±1
0
0 | 0
±1
0 |
0
0
±1 |
1 |
2
2
2 |
6 |
12 | ±1
±1
0
| ±1
0
±1 |
0
±1
±1 |
2 |
4
4
4 |
12 |
24 | | ±1 |
±1 | ±1 |
3 | |
8 | 16 |
±2
0
0 | 0
±2
0 |
0
0
±2 |
4 |
2
2
2 |
6 |
12 |
| Weiter ohne Details | | 2
| 1 | 0 |
5 | |
| 48 |
| 2 | 1 | 1 |
6 | |
| ? |
| 2 | 2 | 0 |
8 | |
| ? |
| 2 | 2 | 1 |
9 | |
|
? |
| 3 | 0 | 0 |
| |
und so wie weiter? |
|
 |
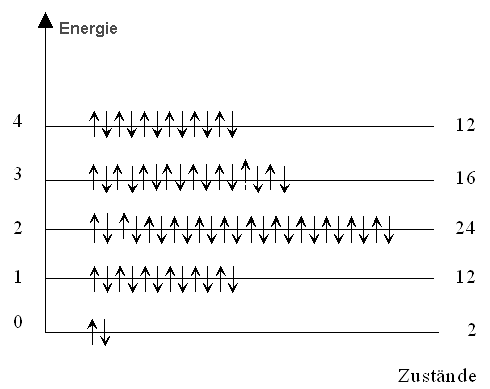
Damit das ganz klar wird, zeichnen wir jetzt das Energie- und Besetzungsschema
für die ersten 5 Zustände: |
|
|
|
 |
Spannend - offenbar ist weder die Abfolge
der Energieneiveaus noch die Zustandsdichte eine triviale Größe; jedenfalls ist aus der Abzählerei kein sofort erkennbares einfaches Bildungsgesetz ableitbar! |
 |
Wir müssen anders vorgehen - wir brauchen den Zustandsraum.
Wir definieren ihn erst mal, und sehen uns dann an, was man damit machen kann. |
|
 |
Der Zustandsraum (auch k-Raum, Phasenraum
oder Impulsraum genannt) ist der Raum, der von den Wellenvektoren aufgespannt wird. Man
stellt sich ihn am einfachsten vor als ein kubisches Gitter
mit den Basisvektoren |
| |
| kx | = |
æ
è |
2p
L |
| 0 | |
0 | ÷
ø |
| | | |
| | |
| | |
| ky | = |
æ
è | 0 |
| 2p
L | | 0 |
÷
ø | | |
| | |
| | |
| |
| kx | = |
æ
è | 0 |
| 0 | |
2p
L |
÷
ø |
|
|
|
 |
Die Einheitszelle hat dann ein Volumen |
| |
|
 |
Jeder erlaubte Zustand des freien Elektronengases entspricht damit einem Translationsvektor in diesem Gitter, der ja identisch ist mit einem der erlaubten Wellenvektoren
|
| |
| k = |
2p
L |
· ( nx, ny, nz ) |
|
|
 |
Nochmal: Der Endpunkt des k-Vektors definiert eine
bestimmte Zelle des Zustandsraums und damit einen bestimmtem Zustand. |
|
 |
In jede Zelle des Zustandraumes passen nach dem Pauli-Prinzip genau zwei Elektronenzustände,
außerdem hat jede Zelle eine definierte Energie gegeben durch die bereits abgeleitete
Formel |
| |
| E | = |
 2 · k2 2 · k2
2me |
|
|
 |
Damit sehen wir sofort: Alle Zellen im Zustandsraum, die den gleichen Abstand
zum Nullpunkt haben, d.h. dasselbe k2, gehören zur gleichen Energie. Anders ausgedrückt:
|
|
 |
Kugelschalen im Zustandsraum sind Flächen identischer Energie. |
|
 |
Das schauen wir uns mal an: |
|
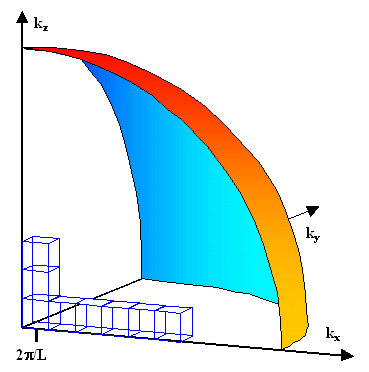 |
Darstellung eines Achtels des Zustandsraumes, der sich
aus den
eingezeichneten Zellen mit dem Volumen (2p / L)3 zusammensetzt.
Das Kugelschalensegment ist eine Fläche konstanter Energie. |
|
 |
Das Rezept zur Berechnung der Zustandsdichte ist jetzt klar - oder? |
|
 |
Die Zahl der Zustände mit derselben Energie im Energieinterval E, E
+ DE ist schlicht die Zahl der Zellen in diesem Intervall. Im Zustandsraum
entspricht das Energieintervall einer "Zwiebelschale" mit Dicke Dk. Das
wollen wir mal berechnen. |
|
 |
Wir betrachten eine Kugel im Zustandsraum mit dem Radius k und dem Volumen |
| |
|
|
 |
Die Zahl
N der Elektronenzustände in dieser Kugel ist gleich der doppelten Zahl der Zellen die in die Kugel passen,
dividiert durch das Volumen der Einheitszelle; wir haben N = 2V(k)/VEZ
oder |
| |
| N(k) = 2 · | |
4p · k3
3 | | | =
|
Vkrist · k3
3p2 |
|
æ
ç
è |
2p
L |
ö
÷
ø |
3 |
|
|
|
 |
Vkrist = L3 ist dabei das Raumvolumen
des betrachteten Kristalls; nicht zu verwechseln mit den Volumina im k-Raum! |
| |
|
 |
Wir definieren jetzt formal dieZustandsdichte
D(E): |
|
 |
Sie ist gegeben durch die Zahl der Zustände in einer
Kugelschale (= 2 × Zahl der Einheitszellen in der Kugelschale) pro Energieintervall
und pro Volumen. |
|
 |
Das ist aber nichts anderes als die Differenz der Zahl
der Zustände in einer Kugel mit Radius E + DE und einer Kugel mit Radius
E dividiert durch Energieinterval DE und (Kristall)volumen
V = L3. In Formeln haben wir |
|
|
| D(E) = |
1
Vkrist |
· |
N(E + DE) – N(E)
DE | = |
1
Vkrist |
· | dN(E)
dE |
|
|
 |
Wir müssen jetzt nur noch N(k) von
oben durch N(E) ersetzen - die Beziehung zwischen k und
E haben wir - und erhalten |
|
|
| N(E) = |
Vkrist
3p2 |
æ
ç
è |
2 · me · E
 2 2 | ö
÷
ø |
3/2 |
|
|
 |
Damit ergibt sich (durch Differenzieren) für die Zustandsdichte des freien Elektronengases |
|
|
| D(E) = |
(2 · me)3/2
2 · p2 ·  3 3 |
· E 1/2 |
|
|
 |
Das ist, wie wir noch sehen werden, ein erstes übergreifendes
und sehr wichtiges Ergebnis aus unserem Modell des freien Elektronengas. |
|
 |
Sehr befriedigend ist, daß sich das Volumen V = L3 des
Kristalls herauskürzt - unser Ergebnis ist ganz allgemein, und nicht mehr von der willkürlichen Größe
des Kristalls abhängig. |
|
 |
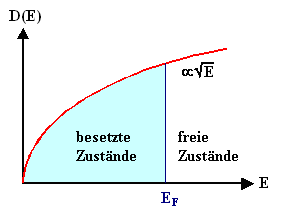
Ansonsten haben wir eine Proportionalität von D zur Wurzel
aus E - das sollten wir uns merken. |
|
 |
Die Einheit der Zustandsdichte ist |
|
|
|
 |
Wenn man das Konzept des Zustandsraums
erst mal kapiert hat, und sich an einige Grundbegriffe der Quantentheorie erinnert, wie z. B. die Heisenbergsche
Unschärferelation, kann man die Zustandsdichte auch in wenigen Zeilen direkt ableiten; der Link
zeigt wie es geht. |
 |
Mit der so definierten Zustandsdichte D(E)
und der obigen Formel (oder mit jeder anderen quantitativen Beziehung) können wir jetzt zum Beispiel die Volumendichte
ze(E) der Elektronenzustände im Energieintervall
{E, E + DE} oder die Zahl der
Elektronenzustände g(E) in diesem Energieintervall DE
ausrechen, es gilt einfach |
| |
| ze(E) | = |
D(E) · DE
| | | |
| | g(E) |
= |
L3 · D(E) · DE |
|
|
 |
Aussehen tut das ganze wie unten gezeigt. Aber zwei Punkte müssen noch erwähnt
werden: |
 |
Damit ist eigentlich alles gesagt, aber es ist manchmal bequemer, die Zustandsdichte
in einer Form auszudrücken, die N(E), d.h. die Gesamtzahl der Zustände bis zur Energie E
als Variable enthält. |
|
 |
Die entsprechende Formel ist mit einem kleinen Trick leicht abzuleiten. Wir nehmen
den ln aus der Formel für die Zahl N(E) der Elektronenzustände
bis zur Energie E und erhalten |
|
|
| ln N(E) | = |
3
2 | · ln E + const. |
|
Þ |
dN
N | = |
3
2 | · |
dE
E |
|
|
|
 |
Daraus folgt sofort |
|
|
| D(E) = | 1
V |
dN
dE | = |
1
V |
3N(E)
2E |
|
|
|
 |
Das ist jetzt zwar ein geschachtelter Ausdruck, da N ja von E
abhängt, aber viel einfacher (und allgemeiner) als die volle Formel. |
 |
Wie realistisch ist die berechnete Zustandsdichte des freien Elektronengases,
oder, in anderen Worten: Wie sehen die Zustandsdichten realer Elektronen in realen Materialien
aus? |
|
 |
Nun ja - meist ziemlich kompliziert; wir werden noch auf viele Beispiele stoßen. Der
Verlauf über die Energie ist nicht eine schöne Parabelfunktion, sondern ein mehr oder weniger wildes Gezappel,
bei dem aber die Parabel immer noch zugrunde liegt. |
|
 |
Aber das macht nichts! Entscheidend ist: Es gibt eine wohldefinierte Zustandsdichte und sie
errechnet sich im Prinzip auch wie gehabt. Nur unsere Wellenfunktionen, und damit die Verteilung der Zustände im k-Raum,
sind komplizierter. |
|
 |
Wir werden bald sehen, daß es für die meisten Fragestellungen auf die genaue Form
der Zustandsdichte sowieso nicht ankommt - im Zweifel nehmen wir immer die einfache Funktion für das freie Elektronengas. |
| |
|
|
Von einem Elektron zu vielen
Elektronen |
| |
|
 |
Im Prinzip haben wir für ein
Elektron gerechnet. Wir haben aber auch unterstellt, daß die Elektronen sich gegenseitig nicht "sehen",
d.h. wir dürfen wie bei der Behandlung der Atome,
jetzt viele Elektronen auf die vorhandenen Zustände verteilen,
denn das Ergebnis gilt für jedes Elektron unabhängig von den anderen. |
|
 |
Entsprechend dem Pauli-Prinzip werden alle Zustände
des Zustandsraumes mit Elektronen besetzt, bis alle in dem betrachteten Festkörper
vorhandenen Elektronen untergebracht sind. |
|
 |
Es werden also alle Zustände einer Kugel mit einem maximalen Radius kF
im Zustandraum aufgefüllt. Fängt man bei kleinen k- Werten an, hat man irgendwann - eben beim Radius
kF - alle Elektronen untergebracht. Dann ist  kF der maximale Impuls den
ein Elektron haben wird. kF der maximale Impuls den
ein Elektron haben wird. |
 |
Dem maximalen Impuls kF der Elektronen
entspricht dann eine maximale Energie; das ist die Energie des "letzten" Elektrons, das wir einfüllen (immer
bei T = 0 K; wir werden gleich sehen warum das betont wird). Diese Energie nennen wir Fermienergie
EF. |
|
 |
Die Fermienergie eines Systems ist eine Zahl
mit einer Einheit [eV], sie ist wie die Zustandsdichte (die eine Funktion ist)
eine, wenn nicht sogar die fundamentale Größe eines Systems mit Elektronen. |
|
 |
In der Kugel mit Radius kF lassen sich damit alle N
Elektronen des Festkörpers der Größe L3 auf Elektronenzuständen unterbringen.
Damit können wir die Fermienergie auch über kF ausdrücken, denn wir haben im freien
Elektronengasmodell eine feste Beziehung zwischen E und k. Wir erhalten
|
| |
| EF | = |
 2 2
2me |
· kF2 |
|
|
 |
Wir können kF noch durch N/Vkrist
= ne, der Volumendichte der Elektronen im System ausdrücken. |
|
 |
Dazu müssen wir lediglich bemerken, dass der "Fermiewellenvektor"
kF identisch ist mit dem Radius der Kugel im k-Raum, die gerade N Zustände
(oder halb so viel Gitterpunkte) enthält. Die Gleichung dazu haben wir bereits, eingesetzt
erhalten wir |
| |
| EF | = |
 2 2
2me |
æ
ç
è |
3p2 · ne |
ö
÷
ø | 2/3 |
|
|
|
 |
Mit ne = N0/ L3 =
(Volumen)dichte der freien Elektronen (in m– 3) des betrachteten Systems. Da wir die Volumendichten
der freien Elektronen halbwegs kennen (wir haben z.B ein Elektron pro Atom für Alkalikristalle, 2 für Erdakalikristalle
usw.) könnten wir die Fermienergie jetzt sogar ausrechnen bzw. abschätzen. Das könnte aber (noch) nicht besonders
sinnvoll sein, da sie sich ja auf einen recht willkürlich definierten Nullpunkt der Energieskala beziehen würde. |
|
 |
Aber was soll's; Übung macht bekanntlich den Meister oder besser Master;
man kann ja mal schnell rechnen |
|
|
|
 |
Weiterhin können wir (hier noch mehr spasseshalber) eine
Fermitemperatur definieren, indem wir einfach die allgemeine thermische Energie kB·T
gleich der Fermienergie setzen, das ergibt |
|
|
|
|
 |
kB ist dabei die Boltzmannkonstante;
nicht zu verwechseln mit dem Wellenvektor!!! Wir werden aber das B
an kB zukünftig wieder weglassen -
k und k unterscheiden sich durch kursive und nicht kursive Schreibweise.
|
 |
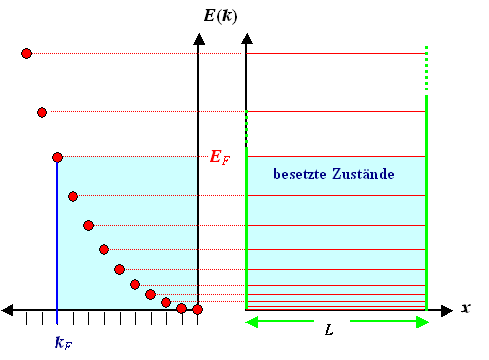
Stellen wir die Ergebnisse noch schnell graphisch dar, erhalten wir das folgende
Bild: |
| |
|
|
 |
Da sich im "Potentialtopf" sehr viele freien Elektronen befinden (bei einem Metallstück
mit der Masse im Gramm-Bereich ca. 1023 Elektronen), liegen die Energieniveaus sehr dicht. Die Energien
des freien Elektronengases sind daher letztlich quasikontinuierlich verteilt.
|
|
 |
Das sieht zwar im obigen Bild nicht so aus (es gibt eher weniger Zustände mit zunehmender
Energie), aber das ist (mal wieder) ein Artefakt der vereinfachten, nämlich eindimensionalen Darstellung. Dreidimensional
sähe es ganz anders aus! |
 |
Wir haben jetzt natürlich noch eine wesentliche
Frage: |
|
 |
Wir haben die Zustände von "unten" her kommend systematisch aufgefüllt,
d.h. wir haben die Energie des Systems minimiert. Dies ist aber nur bei T = 0
K die richtige Minimierungsvorschrift! Wie ist nun die Besetzung der Zustände bei endlicher Temperatur, d.h. wenn
wir dem System etwas thermische Energie zuführen und dann die Entropie, d.h. die
für das Minimum der freien Enthalpie notwendige Unordnung, berücksichtigen
müssen? |
|
 |
Wir müssen jetzt die freie Enthalpie minimieren (wir setzen konstanten Druck voraus) - und das ist eine ganz andere Sache, wie
wir schon früher gesehen haben. |
 |
Die Frage ist leicht, die Antwort schwierig; sie führt uns auf das nächste
Unterkapitel |
| |
|
© H. Föll (MaWi 2 Skript)