|
Die Näherungen des Modells |
| | |
 |
1.
Ein-Elektron-Näherung |
|
 |
Anstelle des Gesamtsystems aus ca. 1023 Elektronen (pro Mol)
betrachtet man ein extrem reduziertes System, bestehend aus einem Elektron. Die restlichen
Elektronen (bestehend aus den Kollegen in einem Energieband und den Rumpfionen des Metalls) werden alle als ein im Mittel
konstantes zusätzliches Potential betrachtet. Das bedeutet, daß die individuelle
Wechselwirkung der Elektronen untereinander vernachlässigt wird - wir nehmen nur an, daß sie sich irgendwie im
Raum gleichmäßig verteilen. Was dann für ein Elektron herauskommen wird,
gilt dann eben auch für alle anderen. |
 |
2. Beschränkung auf freie Elektronen. |
|
 |
Betrachtet werden nur die äußeren Elektronen der Atome - nur die Elektronen auf
Orbitalen, die überhaupt von den anderen Atomen, d.h. der Kristallbindung etwas "merken". Atomkern und innere
Elektronen werden vernachlässigt. Sie bilden ein statisches Hintergrundpotential für die freien Elektronen. |
 |
3.
Konstantes Potential |
|
 |
Im Prinzip müßte man jetzt zur Lösung der Schrödingergleichung für
das eine noch betrachtete Elektron das im Raum periodisch variierende Potential einsetzen,
wie es unten gezeichnet ist plus ein konstantes Zusatzpotential von den "Hintergrundelektronen". |
|
 |
Das ist uns aber noch zu schwierig (obwohl das mathematisch schon machbar
wäre), und wir verwenden einfach ein konstantes (Kasten)potential als (heftige, aber wie sich zeigen wird, sinnvolle)
Näherung. Das sind die blauen Linien in der Zeichnung unten. Wir arbeiten auch grundsätzlich mit einem endlichen
Kristall; in x-Richtung hat er, wie gezeigt, die Länge L. |
| | |
| |
|
| |
|
 |
4.
Periodische Randbedingungen. |
|
 |
Wie groß sind echte Kristalle? Für allgemeine Betrachtungen ist die Vorgabe einer
Größe, z.B der Kantenlänge L, ja nicht besonders sinnvoll - allgemeine Wahrheiten können
ja wohl kaum von der willkürlichen Größe des Körpers abhängen. |
|
 |
Der übliche Trick in solchen Fällen ist: Der Festkörper wird als unendlich
ausgedehnt beschrieben. Leider geht das im Modell des freien Elektronengases mathematisch nicht - die Lösungen
der S.-Gleichungen sind dann einfach alle nur noch y = 0. |
|
 |
Der in solchen Fällen anzuwendende Trick ist aber auch wohlbekannt und besteht darin,
einen endliche Körper gedanklich so zu verbiegen, daß sein Ende auf den Anfang fällt. Kein Problem mit einem
eindimensionalen mathematischen Kristall der Länge L, der einfach
einen Abfolge von Punkten im Abstand a = Gitterkonstante ist. Wir biegen die Punktlinie zu einem Kreis, der
sich selbst in den A... beißt; im Link kann
man sich das (plus Rechnung dazu) ansehen |
|
 |
Um das ganze dreidimensional zu sehen,
muß man sich auch mächtig das Hirn verbiegen (und selbst dann klappt es ohne die Nachhilfe mit gewissen chemischen
Substanzen, die man z.B aus Trauben gewinnt, nicht so recht), oder schlicht die ganz simple mathematische Formulierung hinschreiben: |
| |
| y(x + L, y + L, z + L) = y(x,y,z) |
|
|
 |
In Worten: Die gesuchte Wellenfunktion y muß am Anfang
und Ende des Kristall für jede Koordinatenrichtung denselben Wert haben. |
 |
Diese Gleichung definiert sogenannte periodische
Randbedingungen für die Wellenfunktion y(x,y,z) und macht unseren
endliche Kristall mit der Kantenlänge L zu einem für das zu lösende Problem letztlich unendlich
ausgedehnten Gebilde. |
|
 |
Darf man das? Ja - man darf! In der Herleitung von Theorien
darf man zunächst alles - das einzige Kriterium ist der Erfolg. Der Erfolg in unserem
Fall zeigt sich (später) dann u.a. anderem darin, daß die Schlußfolgerungen, die wir ziehen können,
dann gar nicht mehr von L oder den genauen Randbedingungen abhängen. Aber das können wir jetzt noch
nicht wissen, jetzt rechnen wir einfach mal los. |
|
|
|
Lösung der Schrödingergleichung
für das freie Elektronengas |
| |
|
 |
Für unser Problem genügt die uns bereits
bekannte zeitunabhängige
Schrödinger-Gleichung; die zeitabhängige
Schrödingergleichung ist in einem advanced Modul dargestellt. Für
unseren Fall eines Kastenpotential lautet sie (zunächst eindimensional): |
| |
| – |
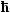 2 2
2me |
· |
d2y(x)
dx2 |
+ V(x) · y(x) |
= |
E · y(x) |
|
|
|
 |
Für das Potential gilt |
|
|
| V(x) | = |
{ |
V0 = const. ( = 0)
¥ |
für 0 £ x
£ L
sonst |
|
|
 |
Im Modell der freien Elektronen beginnt man die Energieskala meist bei der konstanten
potentiellen Energie, d.h. man wählt E = E ' – V0,
oder, wie oben angedeutet, schlicht V0 = 0; wir erhalten |
| |
| – |
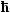 2 2
2me | · |
d2y(x)
dx2 |
= |
E · y(x) |
|
|
|
 |
In dieser Gleichung bedeutet E nach wie vor die (konstante)
Gesamtenergie des Elektrons, aber da die potentielle Energie = 0 ist, beschreibt
E jetzt automatisch nur noch die kinetische Energie des
Elektrons. |
|
 |
Für die y- und z- Richtung gilt natürlich genau dieselbe
Gleichung. |
 |
Die Lösung der Differentialgleichung ist einfach; man erhält |
| |
| y(r) | = |
æ
ç
è |
1
L |
ö
÷
ø | 3/2 |
· exp | (i · k · r) |
|
|
|
 |
Mit r = (x,y,z) = Ortsvektor, und k
= noch unspezifizierter Vektor, den wir mal Wellenvektor nennen, mit
der offenkundigen Dimension [k] =1/cm . |
|
 |
(1/L)3/2 ist ein Normierungsfaktor;
er ergibt sich aus der Normierungsbedingung
|
| |
L
ó
õ
0 |
L
ó
õ
0 |
L
ó
õ
0 |
y(r) · y*(r)
· dxdydz = 1 |
|
|
 |
Dass die gebene Funktion die Lösung der S.-Gleichung ist, ist bisher natürlich
nur eine Behauptung. Ob die Behauptung stimmt, wird sich durch Einsetzen zeigen. Das machen wir aber in einer Übung
weiter unten. |
 |
Das Ergebnis ist, daß die angegebene Funktion dann und nur
dann eine Lösung ist, falls die in der Lösung vorkommenden Größen Gesamtenergie
E, und Wellenvektor
k bestimmte Bedingungen erfüllen. |
|
 |
Welche physikalische Bedeutung dieser Wellenvektor genau
hat, wird sich uns nach und nach erschließen. Der Name deutet aber schon an, wohin die Reise gehen wird. |
 |
Unsere Lösung für ein in einen Potentialkasten eingesperrtes
Elektron hat selbst in dieser allgemeinen und noch unspezifischen Form eine überaus interessante Eigenschaft: |
|
 |
Die Aufenthaltswahrscheinlicheit für dieses Elektron ist überall
dieselbe, denn wenn wir y·y* bilden, erhalten wir
|
| |
| y(r) · y*(r) |
= | æ
ç
è
| 1
L |
ö
÷
ø | 3 |
· exp | (i · k · r) |
· exp | –(i · k · r) |
= | æ
ç
è
| 1
L |
ö
÷
ø |
3 |
|
|
|
 |
Wenn wir das Elektron "suchen", d.h. mit einer geeigneten Meßvorrichtung
"nachschauen", werden wir es überall mit gleicher Wahrscheinlichkeit finden.
Wir sagen: Das Elektron ist über den ganze Kristall "ausgeschmiert". |
|
 |
Das ist ein ziemlich ungewöhnliches Ergebnis, nicht vereinbar mit dem intuitiven Bild
des Elektrons als eines kleinen Kügelchens. Man ist vielleicht geneigt, das als "Artefakt", als künstliches
Ergebnis der Näherungen zu betrachten, aber das wäre genauso falsch, wie anzunehmen, dass das reale Kügelchen
"Elektron" jetzt nur so schnell durch den Kristall saust, dass es uns verschmiert vorkommt (etwa so wie ein Flugeugpropeller,
den man ja auch "verschmiert" sieht). Im Übrigen haben wir die Lösung eines verwandten Problems, nämlich
das in einen zweidimensionalen runden Kasten eingesperrte Elektron, schon
mal angeguckt! |
|
 |
Die "ausgeschmierte" Wellenfunktion ist das
Elektron; auch ohne Näherungen wird sich daran nicht viel ändern. Dem Elektron andere Eigenschaften oder Attribute
zuzuschreiben, außer den in der Wellenfunktion codierten (und natürlich den Grundparametern Masse, Ladung, Spin),
ist genau so sinnvoll, wie zu behaupten, dass das Elektron fromm sei, grün-rot gestreift, und an klassischer Musik
interessiert. Man kann das tun, aber es ändert nichts an dem was man messen kann - und mehr als das existiert in der
Physik schlicht nicht. |
 |
Der Wellenvektor k ist aber kein beliebiger
Vektor, sondern muß Bedingungen erfüllen, die aus den bisher nicht betrachteten periodischen Randbedingungen
folgen. Wir erhalten für die Komponenten des Wellenvektors k = (kx,ky,kz)
für die nur Lösungen existieren |
| |
|
| kx = ± |
nx · 2p
L | |
ky = ± |
ny · 2p
L | |
kz = ± |
nz · 2p
L |
| ni = 0, ± 1, ± 2, ± 3, ..... |
|
|
|
 |
Dabei sind die nx, ny, nz
natürliche Zahlen (inklusive der 0) - sie sind die Quantenzahlen
des Systems. |
|
 |
Jeder mögliche Satz von Quantenzahlen ni, oder,
was gleichbedeutend ist, jeder mögliche k-Vektor, numeriert
einen der möglichen Zustände des Systems.
|
|
 |
Damit haben wir eine erste Eigenschaft von k: Ein Wellenvektor beschreibt einen definierten Zustand des
Systems; er ist eine Art vektorielle Quantenzahl. |
 |
Weiterhin gehört zu jeder Lösung, definiert durch einen
Satz ni bzw ki, eine ganz bestimmte (hier nur kinetische) Energie E;
gegeben durch |
|
| Ek | = |
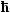 2 · k2 2 · k2
2me |
|
|
 |
Bisher sind das allerdings nur Behauptungen. Daß wir hier wirklich die Lösung
des gegebenen Problems haben, muß erst noch verifiziert werden. Dies ist aber eine rein mathematische
Übung, die wir auch als Übung machen werden. |
|
|
 |
Wir diskutieren jetzt die Lösungen. Wichtig ist wie immer
die Energie. Die Gesamtenergie eines Elektrons in Abhängigkeit von seinem Wellenvektor
(bzw. für den damit beschriebenen Zustand) sieht also so aus: |
|
|
|
 |
Das ist zwar eine triviale Kurve - halt Punkte auf einer Parabel - aber
wir werden das Bildchen noch oft brauchen (und es wird zunehmend komplizierter werden). Energiewerte sind natürlich
nur bei diskreten
k-Werten definiert; zur Klarheit ist aber auch die durchgehende Parabel mit eingezeichnet. |
 |
Funktionen dieser Art, die einen Zusammenhang zwischen einer Energie und einem
Wellenvektor herstellen haben einen Namen: Sie heißen Dispersionfunktion
oder Dispersionsrelation. |
|
 |
Wir wollen uns, falls wir das schon wissen sollten, nicht daran stören, daß auch
Beziehungen zwischen der Frequenz einer Welle und ihrer Wellenlänge
so heißen, oder Beziehunge zwischen Energie und Impuls - es ist letztlich
dasselbe, nur in anderer Form dargestellt. Haben wir z. B. eine Beziehung zwischen Wellenvektor k und
Kreisfrequenz w, macht durchmultiplizieren der Gleichung mit 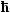 daraus eine Beziehung
zwischen Impuls daraus eine Beziehung
zwischen Impuls 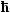 k und Energie k und Energie 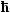 w. w. |
 |
Setzt man für den Wellenvektor k die obige Beziehung in die Energieformel ein, ergibt sich als endgültige Lösung für die "Eigenwerte" der Energie |
|
| Enx, ny,
nz | = |
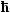 2 2
2me | · |
æ
ç
è |
2 p
L |
ö
÷
ø |
2 | · |
æ
è |
nx2 + ny2 + nz2
| ö
ø |
|
|
|
 |
Die Elektronen können in dem Potentialtopf also nur ganz gestimmte,
diskrete Energien annehmen. Zu jedem Zustand charakterisiert durch einen Satz von 3
ni (oder einem k), gehört also eine bestimmte Energie. Da der Klammerausdruck
mit den ni sich minimal um 1 unterscheiden kann falls man die ni
variiert, haben die Energieniveaus mindestens den Abstand |
|
|
| DEmin = |
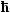 2 2
2me |
æ
ç
è |
2p
L |
ö
÷
ø |
2 |
|
|
|
 |
Allerdings, das sehen wir sofort, können verschiedene
Zustände identische Energien haben - zum Beispiel die Zustände (1,1,1)
und (-1,1,1) oder (2.2,1) und (3,0,0): Sie sind bezüglich der Energie entartet
(es heißt nun mal so!). |
 |
Im Grunde ist jetzt alles klar - außer, daß wir nicht so recht wissen,
was sich hinter dem Wellenvektor k verbirgt. Er ist die zentrale Größe der Lösung -
schau'n mer mal! |
 |
Zunächst erinnern wir uns daran, daß die Energie des Elektrons rein kinetisch ist. Wir können die Energie damit auch wie folgt ausdrücken: |
| |
| E = |
1
2 |
me· v2 |
= |
me2 · v2
2me | = |
p2
2me |
|
|
|
 |
Dabei ist p der (klassische) Impuls des Elektrons. Der Vergleich mit unserer Lösung zeigt sofort: |
| |
| p = |
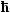 · k · k |
|
|
|
 |
Der Wellenvektor, multipliziert mit "h quer", ist also nichts anderes als
der Impuls des Elektrons - auch in der Quantenmechanik. |
 |
Nun erinnern wir uns an die de
Broglie
Beziehung,
die den Impuls p und die Wellenlänge l verknüpfte: |p|
= h/l. Setzen wir das ein erhalten wir |
| |
| k = |
p
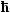 | = | 2p
h | · |
h
l |
= |
2p
l |
|
|
 |
Der Wellenvektor ist also auch sowas wie die reziproke Wellenlänge der dem Elektron zugeordneten "Materiewelle". |
 |
Der Wellenvektor ist aber noch viel mehr: |
|
 |
Er beschreibt den jeweiligen Zustand des Elektrons: Denn
in seiner durch die Lösung der S.-Gleichung erhaltenen Definition stecken die Quantenzahlen ni
des Systems; mit k numerieren wir also auch in etwas codierter (und gleich vektorieller Form) den durch
die Quantenzahlen beschriebenen Zustand des System. Denn die Angabe des Wellenvektors
eines Elektrons reicht vollständig aus um seinen Zustand (d.h. sein Energieniveau und seinen Impuls) eindeutig zu kennzeichnen.
|
|
 |
Diese Eigenschaft hat der Wellenvektor auch dann noch, wenn die einfache Beziehung zwischen
Wellenvektor und Impuls/Energie verloren geht - was passieren wird, sobald wir die extrem simplifizierten Näherung
des freien Elektronengases aufgeben. |
|
 |
Er beschreibt die Richtung und Wellenlänge der Materiewelle: Denn der Ausdruck
|
| |
| exp i(k ·r ) | = |
cos (k · r ) + i · sin (k · r )
|
|
|
|
 |
ist nichts anderes als die mathematische
Codierung einer einfachen ebenen Welle. Die Beziehung |
|
|
|
|
 |
erhalten wir direkt aus dieser Gleichung
- wir brauchen de Broglie gar nicht zu bemühen. Dies bedeutet im Umkehrschluß,
daß die de Broglie Beziehung in unserer Lösung "drinsteckt"; sie ist kein unabhängiges Naturgesetz
sondern in der Schrödingergleichung automatisch enthalten. |
 |
Die Darstellung von Wellen aller Arten
mit einem exp i(k ·r) Ausdruck ist in einem eigenen Modul dargestellt. Wer hier
Schwierigkeiten hat, sollte diesen Modul dringend studieren! |
|
|
|
© H. Föll (MaWi 2 Skript)