|
Mit dem Ausdruck "Eine Welle
" beschreibt man Schwingungsvorgänge im Raum und in der Zeit.
|
|
 |
Schauen wir uns zunächst den Begriff Schwingung
näher an. Eine "Schwingung" allgemeiner
Art nur im Raum liegt immer vor, wenn sich irgendeine Eigenschaft periodisch im
Raum ändert. Das kann die Farbe beim Zebrastreifen sein, es kann aber auch z.B. das periodische Potential U(x
) eines Kristalls sein. |
|
 |
Die Grundeigenschaften einer Schwingung sind in einem extra
Modul dargestellt. |
|
 |
In allgemeinster Form können wir jeden periodischen Vorgang als Fourierreihe
beschreiben und erhalten z.B. für ein periodisches Potential U(x) |
| |
| U(x) | = |
U1 · sin |
2p · x
a |
+ U2 · sin |
2p · 2x
a |
+ U3 · sin |
2p · 3x
a |
+ ... |
|
|
|
 |
Mit a = Gitterkonstante = Wellenlänge
der "Grundfrequenz". |
 |
Ganz allgemein bezeichnen wir
als Schwingung alles, das wie im Beispiel oben nur den Ort als Variable sowie eine
Wellenlänge als Parameter enthält, auch wenn das nicht dem allgemeinen Sprachgebrauch
entspricht (niemand redet im täglichen Leben von der Geländerstangenschwingung oder von Zebraschwingungen bei
Fußgängerüberwegen). |
|
 |
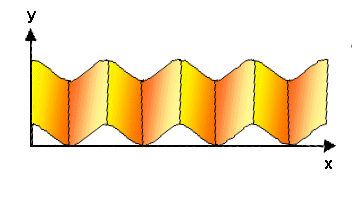
Hier zwei Beispiele: |
|
|
|
 |
Links die langweilige symbolische Darstellung einer Sinusschwingung; rechts eine sehr hübsche
Schwingung, für die man schon eine sehr komplizierte zweidimensionale Fourierdarstellung braucht (wir würden dazu
natürlich unseren alten Trick benutzen und diese Schwingung unendlich ausgedehnt machen, indem wir sie periodisch für
beide Richtungen ins Unendliche fortsetzen). |
 |
Statt dem Ort als Variable können wir aber auch nur
die Zeit nehmen (Ort und Zeit kombinieren wir dann als nächstes). |
|
 |
Eine Schwingung nur in der Zeit
liegt beispielsweise vor, wenn wir die Amplitude A einer stehenden (mechanischen, elektromagnetischen, quantenmechanischen
oder ... ) "Welle" am Punkt r messen. Wir haben in der Fourierreihendarstellung. |
| |
| Ar(t) | = |
Ar, 0 · sin w · t + Ar,
1 · sin 2wt + .. |
|
|
|
 |
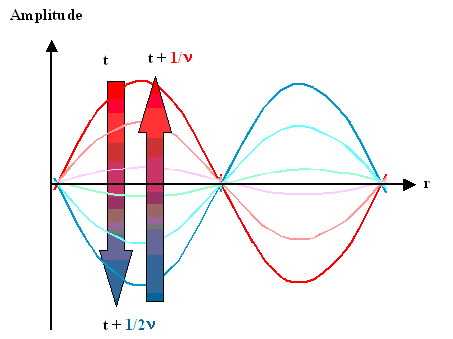
Aussehen kann das so: |
|
|
|
 |
Wir haben eine stehende Welle (eigentlich
müßten wir "stehende Schwingung" sagen), wie man sie z.B bekommt wenn man ein dickes Seil an der Wand
festmacht und dann kräftig "schüttelt"). |
|
 |
Außer der im Raum definierten Wellenlänge, haben wir jetzt auch noch eine Frequenz
n zu berücksichtigen, definiert als der Kehrwert der Zeit die vergeht bis eine Periode
durchgeführt ist, d.h. eine beliebige Ausgangsposition wieder erreicht ist. |
|
 |
Es ist gut, sich hier klar zu machen, daß Wellenlänge und Frequenz
in diesem Beispiel vollkommen unabhängig wählbar sind, sie sind durch keine
allgemeine Beziehung gekoppelt. Für eine konkrete physikalische Anwendung kann
es natürlich eine Beziehung zwischen Wellenlänge und Frequenz geben, das ist dann die Dispersionsfunktion
des jeweiligen Systems. |
 |
Eine Welle
kombiniert im allgemeinen Raum und Zeit. Allerdings unterscheidet niemand, auch nicht
Wissenschaftler, immer sklavisch "Schwingungen" und "Wellen" in voller Strenge - wir haben das gerade
eben auch nicht getan und von stehenden Wellen geredet. |
|
 |
Bei einer "richtigen" Welle gibt es also sowohl periodische zeitliche Änderungen
von was auch immer an einem festen Punkt im Raum, als auch bei einem gegebenen Zeitpunkt periodische Änderungen entlang
einer Richtung im Raum. |
|
 |
Das hört sich kompliziert an, aber jeder weiß was gemeint ist - denn jeder hat
schon genügend laufende Wellen gesehen. Und wenn wir Wellen sagen, meinen wir
im allgemeinen laufende
Wellen, im Gegensatz zu den in der Zeit oder im Raum stationären Schwingungen
oder auch stehenden Wellen. |
|
 |
Aber wie gesagt: So ganz sauber wird selten unterschieden; Schwingungen sind der Grenzfall
von Wellen, und meistens weiß man aus dem Kontext oder aus der Formel eh' was gemeint ist. |
 |
Die Entstehung einer Welle verdeutlicht man (und frau) sich am besten bei der
Betrachtung von Wellen im Ozean, von Schallwellen (die aber nicht so ganz gut zu sehen sind, wohl aber zu hören) oder
aber im schon stark abstrahierten (dafür aber sehr einfachen) Fall von gekoppelten Pendeln |
|
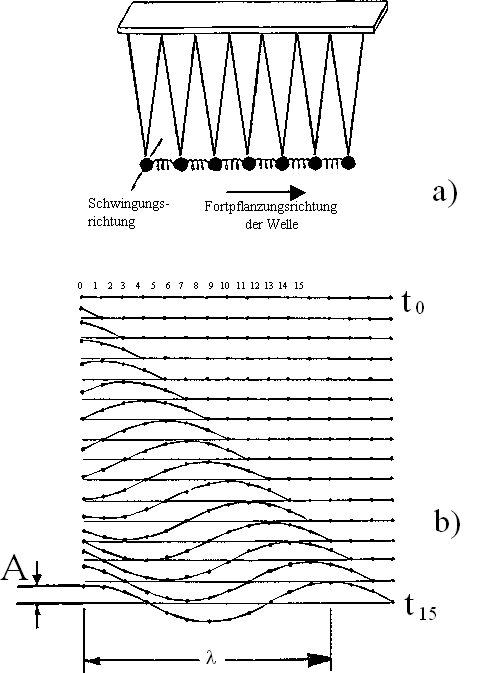 |
| Oben (a): System von gekoppelten Pendeln. Das erste Pendel wird in die gezeigte Richtung ausgelenkt,
die Welle pflanzt sich senkrecht zur Auslenkungsrichtung fort (Transversalwelle). |
| Unten (b):
Momentaufnahmen zu verschiedenen Zeiten (t0 < t15
) des Pendelsystems. Die räumliche Periode der Welle ist l , ihre Amplitude ist
A. |
|
|
 |
Einfache Wellen, i.d.R. solche mit kleinen Auslenkungen oder Amplituden, lassen sich
oft durch eine Sinus-Funktion beschreiben. Die Auslenkung y
als Funktion von Ort und Zeit lautet dann in der mathematisch einfachst möglichen Darstellung |
| |
| y(x, t) | =
| A · sin |
æ
ç
è |
2p · |
æ
è | x
l | – |
n · t | ö
ø
| ö
÷
ø |
|
|
 |
Die Gleichung enthält die drei Bestimmungsstücke
einer Welle: |
|
 |
Die Amplitude A. |
|
 |
Die Wellenlänge
l
. |
|
 |
Die Frequenz
n
oder die PeriodendauerT = 1/n . |
|
 |
Das Argument der Sinusfunktion ist die Phase der Welle.
Man erkennt an der Phase, daß sich die Amplitude der Welle bei einer festen Zeit t mit der Wellenlänge
l wiederholt. Die Frequenz der Welle ist die reziproke Zeit, die von der Welle benötigt wird, um sich um eine Wellenlänge fortzupflanzen. |
 |
Es ist sehr wichtig sich klar zu machen, dass bei dieser einfachst möglichen
Sinuswelle die Wellenlänge und die Frequenz nicht mehr unabhängige Größen
sind. Es gibt eine Beziehung zwischen diesen Parametern, die (notwendigerweise) noch eine 4. Kenngröße
der Welle, nämlich ihre Ausbreitungsgeschwindigkeit (Besser
Phasengeschwindigkeit) v
enthält. |
 |
Dies Beziehung ist leicht herzuleiten: In der Periodendauer T = 1/n hat sich die Welle offenbar genau um eine Wellenlänge l fortgepflanzt.
|
|
 |
Damit definiert sich die Phasengeschwindigkeit
v der Welle als |
| |
|
|
 |
Phasengeschwindigkeit deswegen, weil es ja nur die Phase
ist, die "läuft". Die Welle selbst hat in unserer mathematischen Idealisierung kein Anfang und kein Ende
- sie ist überall schon da. Das einzige was sich "bewegt", ist die Phase. |
|
 |
Man denke an eine Welle auf dem Meer, die in Richtung Strand auf einen zuläuft: Es sind
nicht die Wasser"teilchen" die laufen, auch wenn das so aussieht, es ist die Phase der Welle. Die Wasserteilchen
bleiben in Laufrichtung ortsfest, sie bewegen sich nur auf und ab (außer bei Tsunamis!). |
 |
Für elektromagnetische Wellen im Vakuum haben wir natürlich (???) v = c =
Lichtgeschwindigkeit im Vakuum. |
|
 |
Für andere Wellensorten muß die Ausbreitungsgeschwindigkeit aber aus unabhängigen
Größen ermittelt werden. Die Schallgeschwindigkeit ist beispielsweise keine Naturkonstante oder sonstwie "gegeben",
sondern eine spezifische Eigenschaft des betrachteten Mediums, die sich aus der Wechselwirkung der Atome oder Moleküle
ergibt (bei Festkörpern also mal wieder aus den Bindungen). Bei gleicher Frequenz laufen Schallwellen deshalb verschieden
schnell durch verschiedene Materialien. |
 |
Anstelle der Frequenz n wird aus schreibtechnischen
Gründen häufig die Kreisfrequenz
w verwendet; es gilt |
|
|
|
 |
So wie man statt der Periodendauer T auch die Kreisfrequenz
w = 2p/T verwenden kann, nimmt man statt der Wellenlänge
auch gerne den Wellenvektor k, definiert durch |
| |
|
|
 |
Der Wellenvektor
k wird spätestens bei zweidimensionalen Problemen benutzt, da er zusätzlich zur Wellenlänge
l auch noch die Ausbreitungsrichtung der Welle angibt
(die Richtung des Wellenvektors liegt in der jeweilige Ausbreitungsrichtung). |
|
 |
Damit schreibt sich die Gleichung einer eindimensionalen Welle in x-Richtung. |
| |
| y(x, t) | = |
A · sin (k · x – w · t) |
|
|
 |
Der Übergang zu drei Dimensionen, in
denen sich dann "unsere" Welle in irgendeine räumliche Richtung fortbewegt (und noch ganz andere Wellen möglich
werden) ist jetzt einfach: |
|
 |
Wir verwenden Vektoren, ersetzen x durch
den Ortsvektor r = (x, y, z) und k durch k
= (kx, ky, kz), und erhalten |
| |
| y(r, t) | =
|
A · sin (k · r – w · t)
|
|
|
 |
Die mit dieser Formel beschriebene Welle heißt auch laufende ebene Welle oder kurz ebene Welle; siehe unten. |
| |
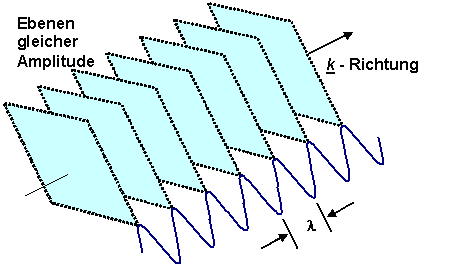 |
Räumliche Darstellung einer ebenen Welle. Die Wellenfront
pflanzt
sich überall in gleicher Weise senkrecht zum Wellenvektor fort. |
|
 |
Ebene Wellen dieser Art haben einige wichtige
allgemeine Eigenschaften: |
|
 |
Entlang einer Wellenfront, die per definitionem senkrecht
zum k-Vektor verläuft und unendlich ausgedehnt ist, herrscht immer
die gleiche Amplitude, da auf der Ebene der Wellenfront das Skalarprodukt k · r konstant
ist. Wer das nicht sofort nachvollziehen kann, sollte sich den Modul über Vektorrechnung
genau ansehen. |
|
 |
Eine mathematische ebene Welle hat keinen Anfang und kein
Ende - weder in der Zeit noch im Raum. Sie kann damit immer nur eine Näherung
an eine reale Welle sein. |
 |
Die
Ausbreitungsgeschwindigkeit ist v = n · l, wie oben schon festgehalten - aber das gilt nur für simple
ebene einfache "Sinus"wellen. Es gilt im Allgemeinen nicht mehr für die
Überlagerungen mehrerer Wellen. |
|
 |
Das kann man am besten einsehen, wenn man sich zwei ebene Wellen vorstellt, die sich nur im
Vorzeichen der Ausbreitungsrichtung unterscheiden und dann überlagern. |
|
 |
Das Ergebnis ist eine stehende Welle, mit einer Ausbreitungsgeschwindigkeit
von Null - obwohl die beiden Teilwellen für sich mit jeder beliebigen Geschwindigkeit laufen können! |
 |
Aber auch für einfache ebene Wellen muß die Ausbreitungsgeschwindigkeit
keinewegs eine Konstante sein. Für elektromagnetische Wellen ist c
zwar die Lichtgeschwindigkeit, aber die ist nur im Vakuum eine absolute Konstante. Im
allgemeinen kann v von der Wellenlänge bzw. Frequenz abhängen. |
|
 |
Der funktionale Zusammenhang zwischen l und n
für eine einfache Sinuswelle, d.h. die Funktion n(l) heißt
Dispersionsrelation. Die Bestimmung der Dispersionsrelation für die interessierenden
Wellen in einem Material ist immer das erste Ziel einer Theorie. |
|
 |
Man kann statt der Beziehung zwischen Frequenz und Wellenlänge genausogut
die Beziehungen zwischen Kreisfrequenz und Wellenvektor, oder Energie (proportional zur Kreisfrequenz) und Wellenvektor,
oder ... nehmen. Großzügig nennen wir die jeweilige Beziehung immer Dispersionsrelation. |
 |
Eine mathematisch elegantere Darstellung einer ebenen Welle benutzt
die komplexen Zahlen; wir erhalten durch Verwendung
der Eulerschen Beziehung die Darstellung |
| |
| y(r , t) | =
|
A · exp [i · (k · r + w ·
t)] = A · exp [i · k · r] · exp [i · w · t] |
|
|
|
 |
Dabei wird in der klassischen Physik bzw. in der Elektrotechnik stillschweigend
vereinbart, daß immer nur der der Real- bzw. der Imaginärteil
die real meßbare Situation beschreibt. |
|
 |
Dies gilt nicht mehr in der Quantentheorie!
Es ist eben eine der Merkwürdigkeiten der Quantentheorie, daß die Wellenfunktion eine "reale" komplexe
Größe ist. Mutter Natur kümmert sich nicht darum, ob wir das verstehen; es ist halt so. |
|
 |
Das ist vielleicht schwer zu akzeptieren, aber das galt für die die irrationalen Zahlen
auch mal.
Pythagoras ließ einen seiner Schüler sogar hinrichten, weil der Ketzer behauptete,
daß es irrationale Zahlen wirklich
gäbe. Heute ist es viel ungefährlicher, seinem Professor zu widersprechen, und auch das ist im Wesentlichen
eine Errungenschaft der Naturwissenschaft/Technik und nicht der Philosophie
. |
| |
|
© H. Föll (MaWi 2 Skript)