2.5.2 Verschiedene Wellensorten

Laufende ebene Wellen

	In Kapitel 2.2.2 haben wir für periodische Randbedingungen für die Wellenfunktion des Elektrons eine laufende, ebene Welle bekommen, beschrieben durch.
		y(r,t)  =  A · exp[i · k · r]  ·  exp [i · w · t]  =  A · exp[i · k · r  +  i · w · t]
	Betrachten wir diese Funktion nun etwas näher. Falls wir nur den Realteil verwerten, erhalten wir
		Re y(r,t)  =  A · cos[ k · r  +  w · t]
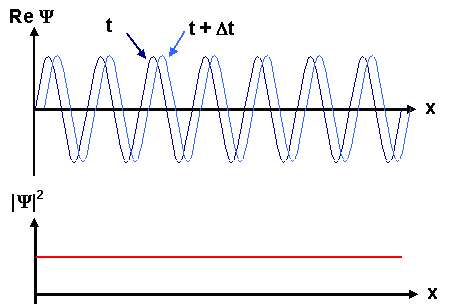
		Es handelt sich also offensichtlich um eine laufende ebene Welle, da die Phase sich linear mit der Zeit ändert. Zu jedem Zeitpunkt ti sieht man eine Momentaufnahme der Welle; etwas später zum Zeitpunkt ti + Dt, hat sich der Sinus etwas "verschoben" - die Welle "läuft"; wie weiter unten dargestellt.
		Für den Imaginärteil gilt natürlich in Prinzip dasselbe.
	In der Quantenmechanik betrachten wir nicht nur den Realteil, denn die Wellenfunktion ist eine intrinsisch komplexe Funktion, d.h. nicht nur aus Gründen der Schreibökonomie.
		Physikalische Bedeutung hat aber (für uns) nur das Betragsquadrat der Wellenfunktion, y · y*; und das ist eine reelle Funtion oder Zahl.
		Wir erhalten:
		y · y*  =  AA*
	Das Betragsquadrat dieser Wellenfunktion ist also eine Konstante, r und t "fliegen raus".
		Damit ist die Aufenthaltwahrscheinlichkeit des Elektrons im betrachteten Raum überall gleich - wir haben das bereits besprochen. Unten ist die Wellenfunktion für zwei verschiedene Zeiten und die Aufenthaltswahrscheinlichkeitsdichte |y|2 dargestellt.

	Stehende Wellen
	Falls wir feste Randbedingungen gewählt hätten, werden wir als Lösung der Schrödingergleichung stehende Wellen bekommen.
		Die Formel dazu sieht so aus:
		y(r,t)  =  exp[+ i · k · r] ·  exp [i · w · t]  ±  exp[– i · k · r] ·  exp [i · w · t]
	Eine stehende Welle ergibt sich danach, falls man zwei Wellen die in entgegengesetzte Richtung laufen überlagert. Wie man das macht ist egal - daher das ± Zeichen.
		Wir haben immer eine hin- und eine zurücklaufenden Welle. Sowohl für die hin- als auch für die rücklaufende Welle werden wir die gleiche Kreisfrequenz finden. Dies liegt an der Inversionssymmetrie, die für alle (pysikalisch sinnvolle) Systeme gilt, also w(k) = w(-k).
		Betrachten wir den Fall mit der + Überlagerung der beiden Wellen, so ergibt sich
		y(r,t)  =  2 ·  cos[k · r]  · exp [i · w · t]
		Der Realteil dieser Funktion zeigt wiederum die Eigenschaften dieser Welle:
		Re y(r,t)  =  2 ·  cos[ k · r]  · cos [ w · t]
		Das Betragsquadrat der Wellenfunktion, also die quantenmechanische Aufenthaltwahrscheinlichkeit von z.B einem Elektron. ist nun nicht mehr konstant im Raum, sondern gegeben durch
		|y|2  =  4 · cos2(k · r)
		Und das sieht für zwei stehende Wellen y1 und y2, mit Frequenz n1 und n2 = 2n1 (oder k2 = 2k1) so aus:
		Die Wahrscheinlichkeitsdichte hat jetzt Maxima und Minima an denen sie = 0 ist.

	Kugelwellen
	Kugelwellen sind Wellen, die sich von einem Punkt aus in alle Richtungen gleichförmig ausbreiten. Zweidimensional kennt das jede und jeder, die/der schon mal einen Stein ins Wasser geworfen hat.
		In der Welt der Physik/Materialwissenschaft treten Kugelwellen aber auch auf wenn man z.B. Licht (oder Elektronenwellen oder Phonen (= Gitterschwingungen) oder ...) an einem "punkt"förmigen Streuzentrum (ein Atom, ein anderes Elementarteilchen, eine Ausscheidung ...) , nun ja, halt streut.
		Jedes denkbare Streuzentrum ist hinreichend punktförmig, wenn es viel kleiner ist als die Wellenlänge der Welle die gestreut wird.
	Die gestreute Welle wird im Nahfeld, d.h. in der Nähe des Streuzentrums, beschrieben durch
		y (| r |, t)  =  1 | r | · exp [i · (|k | · | r|  +  wt)]
		Und das sieht so aus:

	Elektron als Wellenpaket
	Wie beschreibt man nun ein einzelnes Elektron, Proton, Neutron (oder, falls wir gleich verallgemeinern: ein Atom, viele Atome; Herrn Schröder, das Universum); das wir nicht als Lösung der Schrödingergleichung bekommen, sondern von dem wir einfach wissen, daß es sich irgendwo, d.h. an einem halbwegs definierten Ort befindet, und keinesfalls überall gleichzeitig sein kann. Außerdem wird es evtl. auch noch mit einem halbwegs definierten Impuls herumlaufen.
		Eine unendlich ausgedehnte ebene Welle mit konstanter Aufenthaltswahrscheinlichkeit überall kann das einfach nicht leisten.
	Wir beschreiben das so, dass wir den ebenen Wellenterm exp(ikr) behalten, aber das Teilchen trotzdem halbwegs lokalisieren.
		Wir betrachten jetzt also ein Elektron das aus irgendwelchen Gründen nicht mehr gleichmäßig über den ganzen Raum verschmiert ist, sondern in einem mehr oder weniger präzise definierten Raumbereich lokalisiert ist.
		Es hat dann keinen reinen Wellencharakter mehr, sondern verhält sich auch wie ein Teilchen, da es nur in einem bestimmten Raumbereich eine endliche Aufenthaltswahrscheinlichkeit hat.
	Rein mathematisch beschreiben wir das mit einem Wellenpaket, das wir durch eine Überlagerung von ¥ vielen Wellen erhalten. .
		Dazu nehmen wir Wellenvektoren mit verschiedenen Amplituden; d.h. A = A(k) aus einem Intervall [k – Dk/2 , k + Dk/2]
		Die ¥ vielen Wellen werden aufaddiert oder integriert; wir erhalten
		y(| r |, t)  =   k + Dk/2 ó õ k – Dk/2 A(k) · exp[i · (k · r  +  w · t)] · dk
		Jetzt müßte es im Kopf klingeln: Das sieht nicht nur wie eine Fouriertransformierte aus, sondern das ist die Fouriertransformierte des "Spektrums", der Verteilung der Amplituden auf die k-Werte (und damit auch auf die Frequenzwerte).
	Was dabei rauskommt so etwa so aus:
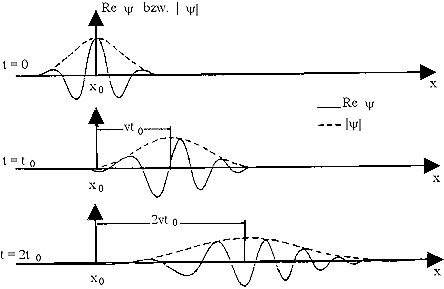		Elektron als Wellenpaket zu verschiedenen Zeiten. Der Realteil der Wellenfunktion ist durchgezogen dargestellt, die Wahrscheinlichkeitsdichte gestrichelt.
	Kann man das einfach verstehen? Ja - wir brauchen nur einen Haufen Sinüsse mit verschiedenen Wellenlängen zu nehmen, die wir so überlagern, daß bei x = 0 alle den Wert 1 haben.
		Die Überlagerung produziert dann bei x = 0 einen ziemlich großen Wert, aber etwas entfernt davon, gibt es nur noch ein wildes Gewusel aller möglichen Werte, die sich gegenseitig aufheben.
		Etwas vornehmer ausgedrückt: Die Fouriertransformierte einer Deltafunktion enthält alle Frequenzen von 0 bis ¥ mit gleicher Amplitude. Engen wir den Frequenzraum ein (indem wir z.B. die Amplitude mit wachsendem Abstand von einer Grundfrequenz auf 0 fahren, ergibt sich ein Wellenpaket.
		Das Wellenpaket hat also eine Unschärfe des Wellenvektor von Dk, und damit eine Impulsunschärfe. Nach der Unschärferelation ist das Elektron daher auf einen endlichen Raumbereich Dx beschränkt, im Gegensatz zum Elektron als laufende Welle, das im gesamten Raum verteilt ist.
	Ein gewisses Problem eines Wellenpaketes ist, daß es im Laufe der Zeit auseinanderlaufen kann (je nach Dispersionsrelation). Dies ist im obigen Bild extrem übertrieben dargestellt (für ein Elektron, das nur so durchs Universum läuft, wären mehrere Alter des Universums erforderlich, bevor es so auseinanderläuft wie dargestellt).

© H. Föll (MaWi 2 Skript)