Merkpunkte Kapitel 2: Elektronen in Festkörpern

	Ohmsches Gesetz			I  µ  U  =  1 R   · U besser: j  =  s  E
	Elektrischer Strom je = mechanischer Strom jT geladener Teilchen			je  =  q · jT   q =  Ladung des Teilchens           jT  =  Zahl Teilchen N pro Fläche F und Zeit t   =   N F · t
	Es zählt nur der Nettostrom = Differenz der Teilströme. Der Nettostrom ist bestimmt durch die Driftgeschwindigkeit vD			j  = q · n · vD
	Damit ergibt sich die "Mastergleichung" für die Leitfähigkeit; µ ist der Materialparameter "Beweglichkeit" = vD/E			s  =  q · n · µ
	Die Existenz einer konstanten Driftgeschwindigkeit trotz einer konstante Kraft erfordert die Existenz von "Reibung" = Stöße im Mikroskopischen.			vD   =  –  E · e · t m               l  =   2t(v0 + vD)               µ   =   vD E   =   e · t m         s   =   n · e2 · t m   =   n · e2 · l 2 · m · (v0 + vD)
		Stoßpartner für die Elektronen sind Phononen, Kristallgitterdefekte und andere Elektronen.
		Die entscheidenden Parameter sind die mittlere Stoßzeit t und die damit verknüpfte mittlere freie Weglänge l
		Es ergeben sich die nebenstehenden Beziehungen.
	Die mittlere thermische Geschwindigkeit v0 folgt aus der klassischen Thermodynamik:			E  =  Ekin =   ½ m · v02 =  3/2 kT v0  =  æ ç è 3 kT m ö ÷ ø 1/2

	Für Metalle mit bekannter Konzentration n der Elektronen und gemessenen Leitfähigkeiten lassen sich die interessanten Größen ausrechnen; man erhält			v0  »  5 · 104 m/s       t  »  4 · 10–14 s       vD  »  6 · 10–1 m/s       l  »  3 nm
		Das kann nicht stimmen - insbesondere l ist viel zu klein!
		Offenbar ist Quantentheorie erforderlich!
		Der Hall Effekt betrachtet Stromfluß im Magnetfeld Bz. Bei orthogonaler Geometrie wird senkrecht zu Ex und Bz eine Hallspannung Ey · Breite induziert.		Ey  =  – µ · Ex · Bz =  RHall · Bz · jx     RHall  =   ± µ s
		Damit sind Beweglichkeiten direkt meßbar; das Vorzeichen der Hallkonstante gibt direkt das Vorzeichen der fließenden Ladungen.
		Gelegentlich findet man positive Ladungen; klassisch nicht erklärbar.Offenbar ist Quantentheorie erforderlich!

	Näherung (= Modell) des freien Elektrongases			Nur ein Elektron; Potential V = const = 0 im Kristall der Länge L; periodischen Randbedingungen
	Ergebnis: Welle mit Amplitude (1/L)3/2			y(r)  =  æ ç è 1 L ö ÷ ø 3/2 · exp (i · k · r)
	Aufenthaltswahrscheinlichkeit überall gleich! Das Elektron ist "ausgeschniert".			y · y* = 1/L3
	Entscheidende Größe ist der Wellenvektor k. Er bestimmt direkt:			kx = ±   ny · 2p L   ky = ±   ny · 2p L   kz = ±   nz · 2p L
		Die "Nummer" (= Quantenzahlsatz) der Lösung.
		Den Impuls p = k.
		Die Gesamtenergie E µ k2.
		Die Wellenlänge l = 2p/k.
	Die Energie ist bezüglich der Quantenzahlen entartet. Die Zustandsdichte D(E) mißt, wieviel Zustände DNe sich in einem Energieintervall DE und im Volumen V befinden.			DNe  = D(E) · DE · V
		Die Zustandsdichte ist über Abzählen im Phasenraum (= Raum der Wellenvektoren) leicht zu berechnen.		D(E)  =   (2 · m)3/2 2 · 3 · p2 · E 1/2
	Beim Auffüllen der Zustände mit Elektronen (bei T = 0 K), wird bei einer definierten Energie - der Fermienergie EF - das letzte Elektron untergebracht sein.			EF  =  2 2me æ ç è 3p2 · ne ö ÷ ø 2/3
		Für eine bekannte Elektronendichte ne ist die Fermienergie leicht berechenbar.
	Zustandsdichte und Fermienergie sind für die elektronischen Eigenschaften realer Kristalle die wichtigsten Kenngrößen überhaupt! Sie sind immer noch wohl definiert, auch wenn die einfachen Modellformeln des freien Elektronengases für reale Kristalle modifiziert werden müssen!

	Fermi-Dirac Verteilungsfunktion			f(E, EF, T) = Wahrscheinlichkeit dafür, daß ein Platz bei der Energie E in einem System mit Fermienergie EF und Temperatur T besetzt ist.
		Damit Wahrscheinlichkeit für Nichtbesetzung		1 – f(E, EF, T)
	Die "Fermi Verteilung" oder "Fermi Statistik" hat die nebenstehende Gestalt:			f(E, T)  =  1 exp æ è E  –   EF kT ö ø + 1 f(E, T) »   exp – E  –   EF kT   für E > EF
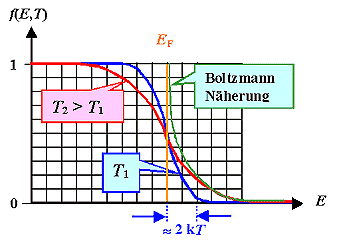		f(E, EF, T) ist eine universelle Funktion die für alle fermionischen Systeme im thermodynamischen Gleichgewicht gilt
		Für den "Hochenergieschwanz" darf man die Boltzmannverteilung verwenden
		f(E = EF) = ½ definiert die Fermienergie
		Der "Aufweichungsbereich" liegt in der Größenordnung kT
	Wichtige Formeln sind			n  =  ¥ ó õ 0 D(E) · f(E,T) · dE n(E1, E2)  =   E2 ó õ E1 D(E) · f(E,T) · dE E(E1, E2)  =  E2 ó õ E1 E · D(E) · f(E,T) · dE
		n  =  Gesamtvolumendichte der Elektronen des Systems.
		n(E1, E2)  =  Volumendichte der Elektronen im gegebenen Energieintervall
		E(E1, E2)  =  Gesamtenergie(volumendichte) im gegebenen Energieintervall
	Dies Gleichungen gelten immer, d.h. nicht nur für das freie Elektronengas. Im realen Kristall unterscheidet sich hier nur die Zustandsdichte von der des freien Elektronengases.

	Molare Wärmekapazität Metall ist klassisch-theoretisch immer			C = Ce  +  CGitter = 6/2 · R  + 3/2 · R =  9/2 · R
		Das ist experimentell doppelt falsch: Gitteranteil geht Þ 0 für T Þ 0 K Elektronenanteil immer << 3/2 · R
		Fehler bei Elektronen: Pauli Prinzip nicht berücksichtigt
	Richtig ist: Nur Elektronen mit freien Plätzen in der Nachbarschaft im k-raum können Energie aufnehmen.			!!! Sehr wichtiges Prinzip !!!
		Das sind nur die Elektronen im "Aufweichungsbereich" der Fermivertteilung

	Richtige Formel			E  =   ¥ ó õ 0 E · D(E) · f(E,T) · dE C  = dE/dT »  D(EF) · ¥ ó õ 0 (E – EF) · d dT æ ç è 1 exp – (E – EF)/kT ö ÷ ø dE  »  p2 2 · R · T  TF
		Strickmuster ist immer: Zustandsdichte mal Fermiverteilung = Dichte Elektronen bei E; mal E = gesamte Energie der Elektronen bei E, Aufsummieren (= integrieren)
		Rechnerei trickreich; braucht Näherungen.

	Schnelle Abschätzung gibt			Ce  » 9NA 2EF  · k2T  =  9/2 R · kT EF  =  9/2 R · T TF
		Merke: Mathe kann schwierig sein, Physik ist aber klar.
	Bei klassischer Leitfähigkeit ebenfalls Fehler weil kein Pauli Prinzip berücksichtigt.			1/2 m · vF2 = k · TF
		Dadurch ist die mittlere Geschwindigkeit v0 viel zu klein
		"Reparatur" klassischer Formel: Ersetze v0(klassisch) durch "Fermigeschwindigkeit vF"
		Damit größere freie Weglängen; grundsätzliches Verständnis möglich.
	Genauer Betrachtung der mittleren freien Weglänge als Funktion von Temperature, Defekten, Legierung usw. ergibt die klassishen "Reglen" und "Gesetze" für die Leitfähigkeit der Metalls.			Matthiesen Regel: r  » r0 (1 + aT)   a »  4 · 10– 3 K– 1 Nordheim Regel: r  µ Konz. Legierungselement
	Fragebogen Multiple Choice Fragen zu Kapitel 2

© H. Föll (MaWi 2 Skript)