Wellen und Phasen

	Hier schnell einige Grundbegriffe der Trigonometrie - was genau ist ein sin(ax)?
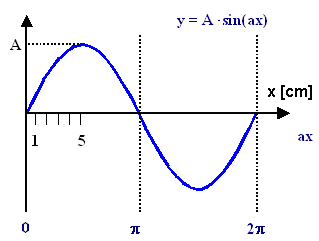
		Ein Sinus beschreibt eine typische Welle (oder, genauer, eine Schwingung) sein Graph sieht am einfachsten so aus wie unten links gezeigt:
		Dabei ist die x-Achse doppelt ausgeführt: Einmal direkt (x), und einmal dunkelblau als a x. Wir schreiben den Sinus als
		y = A · sin(ax)
		Dann ist A die Amplitude; und im Argument des Sinus stecken "irgendwie" Wellenlänge l und Phase f. Die Variable x ist in der Maßeinheit [m] zu nehmen; der Parameter a muß damit die Dimension [1/m] haben.
	Die Wellenlänge ist die Strecke für einen Durchgang und dafür braucht man immer (vielfache von) 2p im Argument des Sinus. Nimmt man die Wellenlänge l statt des Parameters a, schreibt sich der Sinus also so:
		y = A · sin æ ç è 2p l   · x ö ÷ ø l  =  2p a
	Was ist jetzt die Phase dieser Schwingung?
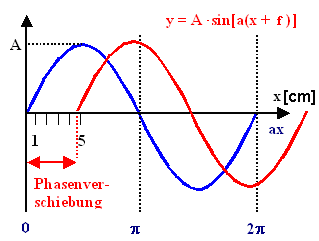
		Das ist eine Frage, die so nicht eindeutig zu beantworten ist, denn die Phase einer Schwingung bezieht sich auf einen definierten Nullpunkt, oder anders gesagt, Phasen sind eigentlich immer Phasendifferenzen.
		Das ist im rechten Bild verdeutlicht, in dem die rote Schwingung gegenüber der blauen phasenverschoben ist. Die rote Schwingung schreibt sich als
		y = A · sin [a · (x + f)]  =  sin æ ç è 2p l   · (x + f) ö ÷ ø
		Dabei ist die Phase als Strecke in [m] zu nehmen. Im obigen Bild ist sie f » 4,7 cm.
	Was machen wir, wenn wir nicht die Phasenverschiebung als Strecke f kennen, sondern im (sinnvolleren) Bogenmaß f. Im Beispiel wäre f » p/2?
		Wir rechnen um, indem wir einfach das Verhältnis der Strecken betrachten. Es gilt:
		f l  =  f 2p               f  =  2p · f l  =   f · a y = A ·  sin æ ç è 2p l   · (x + f) ö ÷ ø  =  A ·  sin æ ç è 2px l   + f ö ÷ ø
	Damit ist klar, wie die Phasenverschiebung in Kap. 3.4.2 auszurechnen ist.
		Weiterhin ist klar, wie sich eine Phasenverschiebung in komplexer Schreibweise darstellt. Unsere "normale Welle sieht so aus
		y(x) = A · exp æ ç è i · 2p l   · x ö ÷ ø Dreidimensional y(r) = A · exp æ ç è i · 2p l   · r ö ÷ ø  =  A · exp(ikr)
	Mit einer Phasenverschiebung f oder f wird daraus

Mit Frame

2.5.1 Eigenschaften von Wellen und Teilchen

3.4.1 Der Strukturfaktor

Volle Herleitung der Bragg-Bedingung

© H. Föll (MaWi 2 Skript)