|
Wir wissen es schon: Das Bragg-Gesetz
k – k' = G gibt nur die Lage der Reflexe
an, nicht aber deren Intensität. |
|
 |
In anderen Worten: Haben wir einen Kristall, eine einfallende Welle und einen
Bildschirm irgendwo, so sagt uns die Bragg-Beziehung zwar wo
auf unserem Bildschirm wir überhaupt damit rechen können, daß gebeugte Wellen auftreffen; aber keineswegs
wie groß die Intensität der dort möglichen Wellen, kurz die Intensität des Reflexes sein wird. |
 |
Schon rein logisch ist klar: Ein mathematisches Gitter wird eine reale Welle überhaupt
nicht beeinflussen, die Streuung von Wellen erfolgt nicht am Gitter, sondern an Atomen. Anders ausgedrückt: |
|
 |
Die Intensität eines möglichen Reflexes ist
durch die Basis bedingt, d.h. durch die Atome die aus einem Gitter
einen Kristall machen; sie kann zunächst mal jeden Wert annehmen. |
|
 |
Insbesondere kann die Intensität auch = 0 sein - d.h. der Reflex ist zwar durch
die Bragg-Bedingung erlaubt, aber man sieht ihn nicht! |
 |
Die Reflexintensitäten werden durch den sogenannten Strukturfaktor
bestimmt. Der Strukturfaktor wiederum ist abhängig von der Art und Verteilung der Atome in der Elementarzelle - d.h.
von der Basis. |
|
 |
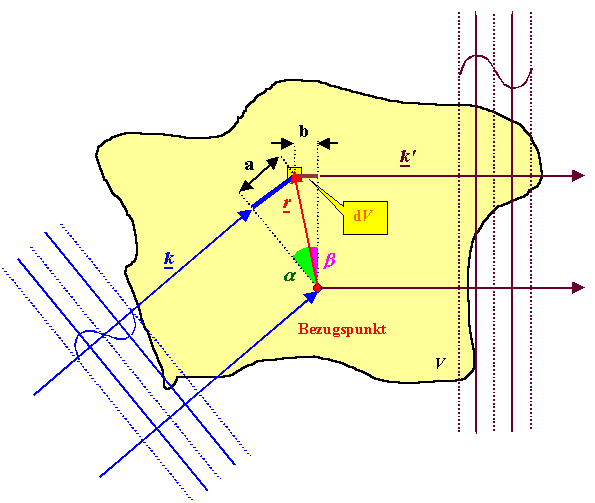
Zu seiner Berechnung müssen wir etwas Aufwand treiben. Dazu betrachten wir die Streuung
einer einfallenden ebenen Welle mit Wellenvektor k an einem beliebigen Streuvolumen
V eines beliebigen Körpers. Das ist unten schematisch gezeigt. |
| |
|
 |
Wir betrachten jetzt die Wechselwirkung der einfallenden ebenen Welle mit den
Atomen des Kristalls in einem differentiell kleinen Volumenelement dV des Streuvolumens am Aufpunkt
r. |
|
 |
Dabei mag eine Kugelwelle oder irgendetwas angeregt werden. Was auch immer von dV
ausgestrahlt wird, wir interessieren uns erstmal ausschließlich für die Komponente, die mit dem Wellenvektor
k' in k' Richtung läuft. |
|
 |
An dieser Stelle ist k' aber noch nicht definiert - wir könnten
jede beliebige Richtung und jeden beliebigen Betrag betrachten. Um einfach weiterzukommen,
müssen wir jetzt aber Annahmen machen bzw. spezielle Fälle betrachten. |
 |
Die erste Eingrenzung ist noch einfach: Wir wollen hier nur elastische Streuung betrachten, d.h. die Energie der Wellen soll sich nicht ändern
und damit muß gelten |
| |
|
|
 |
Wir beschreiben jetzt die einfallende Welle mit W ein = eikr,
d.h aus Gründen der Einfachheit mit einer Amplitude = 1. Dabei ist es noch gleichgültig, um was für
Wellen es sich handelt. Alles was "wellen" kann, ist in der
Gleichung erfaßt. |
 |
Der aus unserem Volumenelement dV kommende in k' Richtung
laufende Teil der gebeugten Welle W ' muß dann so aussehen |
| |
| d W ' | = |
F 'loc( r) · exp (ik'r) |
|
|
|
 |
F 'loc(r) nennen wir die lokale Streuamplitude des
Ortes r. Sie wird natürlich davon abhängen, was genau am Ort r sich
befindet. |
 |
Den gesamten aus V kommenden in k' Richtung
laufenden Teil der gebeugten Welle W ' schreiben wir jetzt einfach als |
| |
|
 |
Zur gesamten Amplitude A tragen
alle Volumenelemente dV bei; wir können A in k' Richtung also durch
Aufsummieren bzw. -integrieren der lokalen
Streuamplituden F 'loc(r) erhalten: |
| |
| A | = const. · |
ó
õ
v |
F 'loc(r) · dV |
|
|
|
 |
Die Konstante vor dem Integral ist hier noch ziemlich witzlos und dient nur
der Schreibökonomie, da wir sie in späteren Gleichungen dann nicht mehr in F'loc
berücksichtigen müssen. |
 |
Der entscheidende Faktor ist also die lokale Streuamplitude
F 'loc. In ihr stecken wiederum zwei Teile: |
 |
1. Ein Term der die Wechselwirkung mit der in dV enthalten
Materie beschreibt. Darüber wissen wir a priori nichts
- wir müssen also eine Annahme machen. |
|
 |
Die Annahme ist einfach für Elektronen- und Röntgenwellen: Die Wechselwirkung der
Atome mit diesen Wellen ist
proportional zur Elektronendichte
r(r ) in dV. |
|
 |
Atome mit hoher Ordnungszahl und damit mit höherer (mittlerer) Elektronendichte streuen
diese Wellen also stärker als leichte Atome - das ist offenkundig keine abwegige Annahme. |
 |
2. Ein Term exp[i · j(r)],
der die Phase
j der gestreuten Welle enthält. Wer das nicht auf Anhieb versteht, betätigt
den Link |
|
 |
Das ist vielleicht nicht auf Anhieb einsichtig, aber wie obiges Bild zeigt, ist die Phase
der in k' Richtung gestreuten Welle von Ort zu Ort verschieden
- und wir müssen das berücksichtigen! |
 |
Damit können wir die lokale Streuamplitude
schreiben als |
| |
| F 'loc(r) |
= const. · |
r(
r ) · exp [i · j(r)] |
= const. · Floc(r) |
|
|
|
 |
Wir machen jetzt also einen Übergang zu einer "ungestrichenen" lokalen Strukturamplitude
da wir die (uninteressante) Proportionalitätskostante wie schon angedeutet vor
dem Integral verstecken (und vergessen) können. |
 |
Das ist die entscheidende Gleichung. Der Rest ist jetzt (ziemlich trickreiche)
Mathematik. |
|
 |
Floc(r) und die Phasenverschiebung j (r)
sind Funktionen des Ortes; wir müssen sie kennen um das Integral auszurechnen. |
 |
Die Phasenverschiebung ist leicht auszurechnen; sie ergibt sich aus der Summe
der Längen a und b in obigem Bild, die ihrerseits geschrieben werden können als
|
| |
| a | = |
|r| · sin a |
| | | |
| b | = |
|r| · sin b |
|
|
 |
Die Länge
a wird zu einer Phase j
a über die elementare Beziehung
a/l = ja/2p, damit erhalten
wir |
| |
| ja = |
2 · a · p
l | = |
2p · |r| · sin a
l |
|
|
|
 |
Der Faktor 2p/l ist natürlich
nichts anderes als |k |; wir können
also auch schreiben
|
| |
| ja = |
|k| · |r| · sin a |
= |k| · |r| · cos(90o – a) | = |
k · r |
| jb = |
| |
|
– k ' · r |
|
|
 |
Die Phasen ergeben sich also einfach aus den Skalarprodukten der Wellenvektoren mit dem Ortsvektor (wobei wir die Herleitung der Beziehung für
jb der Eigeninitiative überlassen; wer zu faul ist schaut in den Link). |
|
 |
Die gesamte Phasenverschiebung j = ja
+ jb ist also |
|
|
|
 |
Wir erhalten damit für die lokale
Streuamplitude Floc(r ) |
| |
| Floc(r) | = |
r(r) · exp [i · r · (k – k')]
|
|
|
|
 |
und für die gesamte Streuamplitude F |
| |
| F | = |
ó
õ
V |
Floc (r) · dV = |
ó
õ
V |
r( r) · eir ·
(k – k ') · dV |
|
|
 |
Das sieht nun sehr wir eine Fouriertransformierte der Ladungsdichte r(r) aus; es ist
nur nicht ganz klar welche Bedeutung dann der neuen Variablen k – k' zukommt. |
|
|
 |
Hier begänne die ernsthafte Herleitung der Beugung in Kristallen. Wir wollen
aber nur die wesentlichen Schritte skizzieren, um dann mit unserem bereits vorhanden Wissen weiterzumachen. Wer will, kann
diesen blauen Block überspringen. |
|
 |
Zunächst überlegt man sich, daß r(r)
immer eine im Raumgitter periodische Funktion sein muß, d.h. r(r
+ T) = r(r). |
|
 |
Damit muß rein mathematisch eine Fourierentwicklung in einem "reziproken"
Raum möglich sein. Wenn man die mathematische Analyse durchführt, "entdeckt" man zwangsläufig das
reziproke Gitter als Fouriertransformierte des Raumgitters. |
|
 |
r(r) wird damit zu |
| |
| r(r) = |
S
nG · ei(G · r) |
| | |
| nG = |
1
V |
ó
õ
V |
r(r) · e– i(G · r)
· dV |
|
|
 |
Setzt man das in die Gleichung für die Strukturamplitude F
ein , erhält man nach einiger Rechnung, daß nur für
k – k' = G ± Dk
die Strukturamplitude wesentlich verschieden ist von 0. |
|
 |
In anderen Worten: Man erhält die Bragg-Bedingung, noch verziert mit
einer zulässigen Abweichung im Wellenvektor, die quantitativ die früher
schon besprochene Ausdehnung der reziproken Gitter"punkte" angibt. |
| |
|
|
 |
L = Ausdehnung des Kristalls. |
 |
Damit hat man den Punkt erreicht, an dem wir jetzt weitermachen. |
 |
In der Formel für die Streuamplitude steht im Exponenten der Ausdruck k
– k', und für k' sind noch beliebige
Richtungen zugelassen (nur der Betrag liegt fest, da wir elastische Streuung behandeln). |
|
 |
Wir wissen aber bereits, daß für alle k'
Werte die nicht der Braggbedingung k – k'
= G, und |k| = |k'| genügen, keine
Beugung stattfindet und damit auch die Amplitude der gebeugten Welle automatisch = 0 ist. |
|
 |
Präziser ausgedrückt: Was auch immer lokal in jedem dV in "falsche";
d.h. nicht der Bragg-Bedigung genügende k' Richtungen gestreut wird - und Streuung findet immer
statt! - wird sich schlicht "weginterferieren" |
 |
Das ist sehr praktisch! Denn
wir müssen die Formel für die Streuamplitude also nicht für alle möglichen k' auswerten,
sondern nur noch in der Form |
|
|
| F | = |
ó
õ
V |
r(r) · exp (i · r · G)
· dV |
|
|
 |
Das ist eine enorme Vereinfachung, da wir jetzt nur noch für eine endliche
Anzahl von reziproken Gittervektoren rechnen müssen (wie schon mehrmals angedeutet, können wir i.d.R. die "großen"
G vernachlässigen). |
|
 |
Wir nennen F jetzt auch nicht mehr Streu
amplitude, sondern Strukturamplitude
Fs, da wir jetzt nur noch Kristalle betrachten (die Formeln für die Streuamplitude gelten
für alle Materialien - amorph, inhomogen, was auch immer). Den Index "s"
lassen wir später aus Bequemlichkeit dann auch noch weg. |
|
 |
Aufzupassen ist aber noch an einer Stelle: Die Intensität
IG der an der Netzebenenschar mit dem reziproken Gittervektor G gebeugten Welle ist
durch das Quadrat der Amplitude gegeben, d.h. wir haben |
| |
|
|
 |
und dabei müssen wir berücksichtigen, daß die Strukturamplitude eine komplexe
Größe ist. Eigentlich hätten wir auch "µ" (proportional)
statt "=" (gleich) schreiben müssen, aber das bringt nur wieder eine für's Prinzip unwichtige (und auch
von der größe von V ) abhängige Konstante. |
| | |
|
Berechnung der Strukturamplitude |
| | |
 |
Die Integration läuft über einen Kristall mit dem Volumen
V. Das Integral kann man nun stark vereinfachen, indem man zunächst nur über das Volumen einer Elementarzelle (EZ) integriert, und anschließend über alle EZ
summiert, d.h. den erhaltenen Wert mit der Zahl der Elementarzellen multipliziert. |
|
 |
Das können wir tun, denn das Integral muß für jede
EZ denselben Wert liefern; sie sind ja alle identisch. Schematisch machen wir folgende Aufspaltung |
| |
ó
õ
V |
= |
S
|
ó
õ
EZ |
= |
V
VEZ |
· |
ó
õ
EZ |
|
|
|
 |
Dabei ist natürlich nur das Integral über die Elementarzelle von Interesse, denn
der Rest liefert mal wieder nur eine lästige Konstante, die wir "vergessen". |
|
 |
Um das verbleibende Integral auszuwerten, kommen wir nun nicht umhin, j
Atome in die EZ "einzufüllen", d.h. eine Basis zu definieren. Der Index j ist damit
eine ganze Zahl, die die Atome numeriert und ihre Art kennzeichnet. |
 |
Eine beliebige Basis definieren wir jetzt also, indem wir einen Nullpunkt wählen
(zweckmäßigerweise eine Ecke der EZ), und den j Atomen je einen Vektor rj
zuweisen, der die Lage des Atoms in der EZ definiert. Damit bekommen wir einen Satz von r
j , der (zusammen mit einer Tabelle der Atomsorten) die Basis eindeutig definiert. |
|
 |
Das klingt abstrakt, ist aber ganz einfach. Die nachfolgenden Beispiele illustrieren
dies: |
| |
| Kristall |
Gittertyp | rj |
Atom | | Fe | bcc | r
1 = (0 0 0)
r2 = (½ ½ ½) |
Fe
Fe | | Al | fcc |
r1 = (0 0 0)
r2 = (½ ½ 0)
r3 = (½ 0 ½ )
r4 = (0 ½ ½ ) |
Al
Al
Al
Al |
| Si | fcc
diamond | r1 = (0 0 0)
r2 = (½ ½ 0)
r3 = (½ 0 ½ )
r4 = (0 ½ ½ )
r5 = (¼ ¼ ¼ )
r6 = (¾ ¾ ¼)
r 7 = (¾ ¼ ¾ )
r8 = (¼ ¾ ¾ ) |
Si
Si
Si
Si
Si
Si
Si
Si |
| GaAs | fcc
diamond | r1 = (0 0 0)
r2 = (½ ½ 0)
r3 = (½ 0 ½ )
r4 = (0 ½ ½ )
r5 = (¼ ¼ ¼ )
r6 = (¾ ¾ ¼)
r 7 = (¾ ¼ ¾ )
r8 = (¼ ¾ ¾ ) |
Ga
Ga
Ga
Ga
As
As
As
As |
|
|
 |
Aber Materialwissenschaftler
geben nicht so leicht auf und haben noch Tricks auf Lager: Wir vereinfachen die Integration über die Elementarzelle! |
|
 |
Wir führen die Integration innerhalb der EZ nur in einer Kugel um die diversen
Atome durch; mit Kugeldurchmesser » Atomradius, und summieren
dann einfach die isgesamt j "Kugel"-Integrale. Das ist im Bild unten für 2 Atome illustriert. |
| |
|
 |
Die Einzelintegrationen laufen jetzt über eine Hilfsvariable r',
die die Umgebung eines Atoms "abtastet". |
|
 |
Damit haben wir natürlich den Bereich zwischen den Atomen nicht berücksichtigt.
Aber dort ist die Elektronendichte sowieso = 0 oder zumindest klein, es wird also nicht viel fehlen. |
|
 |
Wir erhalten dann näherungsweise für die Strukturamplitude
Fs aus einer EZ |
| |
| Fs | = |
S
j
|
ó
õ
V' |
r(rj + r'j) · exp[i(
rj + r'j) · G] · dV' |
|
| Fs | = |
S
j
|
exp[i · rj · G] · |
ó
õ
V' |
r(rj + r'j) · exp[i
· r'j · G] · dV' |
|
|
 |
Damit sind wir am Ende der allgemeinen Überlegungen. Weiter kommt man nur
noch für spezifische Kristalle.Was ist nun konkret zu tun? Erstmals noch eine ganze Menge, wir listen das mal kurz
auf: |
 |
1. Wir wählen den gewünschten Reflex; d.h. einen bestimmten G-Vektor,
z.B. G = (111). Das bedeutet, daß wir jetzt die Intensität der an {111} Ebenen gebeugten
Strahlung bestimmen wollen. In unserer "Versuchsanordnung" ist dabei die Bragg-Bedingung erfüllt, denn das
haben wir in die Formel hineingesteckt - nur dafür gilt sie. |
 |
2. Wir wählen den gewünschten Kristall, d.h. Gittertyp und Basis.
Damit ist der rj-Satz festgelegt und die Elektronendichte um rj
herum - in der jeweils verfügbaren Näherung. |
|
 |
Falls wir über die Elektronendichte eines gebenen Atoms nichts genaues wissen, nehmen
wir in nullter Näherung eine konstante Dichte (= Zahl der Elektronen durch Atomvolumen);
in einer ersten Näherung eine kugelsymmetrische, aber nicht mehr konstante Dichte,
und in einer zweiten Näherung eine Dichte die die Bindungen berücksichtigt - z.B. die Keulen der sp3
Hybridorbitale . |
 |
3. Wir führen jetzt die einzelnen Integrationen durch - zunächst
für alle Arten von Kristallen und Beugungsvektoren. |
 |
Dabei fällt uns aber auf, daß in der Nullten und ersten Näherung
für viele Strukturen immer dasselbe herauskommt (bis auf eine Konstante) - unabhängig
vom gewählten Kristall. Schließlich integrieren wir im wesentlichen nur in einer Kugel herum - wo diese Kugel
in der EZ sitzt und wieviele andere Kugeln noch da sind, ist völlig unerheblich. |
|
 |
Das heißt, wir machen diese Integration nur
einmal - für alle 92 Atome und für die halbwegs niedrig indizierten reziproken Gittervektoren.
Genauer gesagt - wir machen diese Integration gar nicht, denn das wurde längst
gemacht und die Werte sind tabelliert. |
|
 |
Wir definieren deshalb einfach einen Atomformfaktor
f, gegeben durch das bestimmte Integral |
|
|
| fj | = |
ó
õ
V |
r(r'j) · exp [i · r'j
· G] · dV' |
|
|
|
 |
und erhalten damit als vereinfachte Formel für
die Strukturamplitude |
| |
| Fs | = |
S
j |
fj · exp [i · r
j · G] |
|
|
 |
4. Damit berechnen wir jetzt die Strukturamplitude für den gewählten
Reflex durch Aufsummieren der Komponenten. |
 |
Heureka! Die Strukturamplitude ist nun verhältnismäßig einfach
auszurechnen - immer vorausgesetzt, man kennt die Atomformfaktoren fi . Aber wir sind immer noch
nicht fertig: |
|
 |
Wenn man dieses Programm wirklich ausführt, finden sich sogar noch ein paar ganz allgemeine
und extrem nützliche Regeln , die wir im nächsten Unterkapitel anschauen wollen.
Dabei muß man noch nicht mal immer die Atomformfaktoren wirklich ausrechnen. |
 |
Vorher aber noch ein letztes Wort zu den wirklich gemessenen
Intensitäten. |
|
 |
Wir müssen nicht nur eine bisher nicht näher erläuterte
Proportionalitätskonstante bedenken (die z.B. für Elektronen- oder Röntgenstrahlen sehr verschieden sein
wird, sondern auch das beugende Volumen V. |
|
 |
In der Praxis kommt der gebeugte Strahl aber fast nie aus dem gesamten
Volumen der Probe, denn entweder wird unser einfallender (dünner) Strahl gar nicht das gesamte Volumen anregen, oder
die gebeugte Intensität kommt nur aus einigen Körnern unbekannter Größe eines Polykristalls (da nur
dort die Bragg-Bedingung erfüllt ist), oder beides zusammen. |
|
 |
Außerdem hängt die Intensität noch davon ab, wie exakt wir die Bragg-Bedingung
erfüllen. Die Formel für die Strukturamplitude gilt nur für exakte Erfüllung, wir erhalten aber auch
noch Intensität wenn wir knapp danebenliegen. |
 |
In der Praxis sind deshalb die absoluten Intensitäten
nicht so wichtig. Viel wichtiger sind die Intensitäts verhältnisse zwischen
den Reflexen, und das ist es was man mißt und auswertet. |
© H. Föll (MaWi 2 Skript)