|
Formale Definition reziprokes Gitter im 3D: |
|
| g1 = 2p · |
a2 × a3
a1 · (a2 × a3) |
= 2p · |
a2 × a3
V |
| | | | |
| g2 = 2p · |
a3 × a1
a1 · (a2 × a3) |
= 2p · |
a2 × a3
V |
| | | | |
| g3 = 2p · |
a1 × a2
a1 · (a2 × a3) |
= 2p · |
a2 × a2
V |
|
|
|
 |
Liefert identische Vektoren wie die geometrische Konstruktion (plus Vorzeichen) |
|
|
 |
Einfacher (und allgemeiner) ist: |
|
|
| |
|
|
| ai · gj = 2 pdij
= | { |
1 für i = j
0 für i ¹ j |
|
| |
|
| |
| |
 |
Wichtige Eigenschaften des reziproken Gitters: |
|
| Das reziproke Gitter ist die Fouriertransformierte des Ortsgitters
|
|
|
 |
Ghkl senkrecht auf d(hkl). |
|
|
 |
|Ghkl| = 2p/dhkl;
dhkl | |
|
 |
G · T = 2 p ·
n. | |
| |
| |
| |
 |
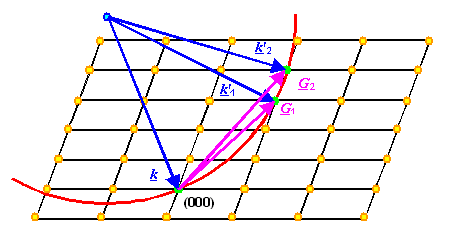
Ewaldkugel-Konstruktion für Beugung: |
|
|
|
 |
Erlaubt schnelle und einfache Betrachtung aller Varianten von Beugungsexperimenten. |
|
|
 |
Hier für monochromatische Strahlung gezeigt. |
|
© H. Föll (MaWi 2 Skript)