3.3.3 Zusammenfassung Kapitel 3.3

	Reziproke Gittervektoren Ghkl werden formal definiert als Translationsvektoren im reziproken Gitter.
		Das reziproke Gitter ist in eineindeutiger Weise aus einem beliebigen Raumgitter mit den Basisvektoren ai konstruierbar; seine Basisvektoren gi sind (im dreidimensionalen) gegeben durch
		g1 =  2p · a2 × a3 a1 · (a2 × a3) =  2p · a2 × a3 V         g2 =  2p · a3 × a1 a1 · (a2 × a3) =  2p · a2 × a3 V         g3 =  2p · a1 × a2 a1 · (a2 × a3) =  2p · a2 × a2 V
	Das reziproke Gitter ist die Fouriertransformierte des Ortsgitters. Es hat wichtige Eigenschaften:
		1. Ghkl = h · g1 + k · g2 + l · g3 steht senkrecht auf der Ebene des Raumgitters mit dem Miller Indizes (hkl)
		2. |Ghkl| = 2p/dhkl; dhkl ist der Abstand der Netzebenen.
		3. Das Skalarprodukt zwischen einem beliebigen Translationsvektor T des Raumgitters und einem beliebigen Translationsvektor des zugehörigen reziproken Gitters ist immer (mit n = 0, 1, 2, 3, ...).
		G · T  =  2 p · n
		4. Es gilt immer (mit dij  = Kronecker Symbol)
		ai · gj = 2 p dij  =  { 1 für i = j 0 für i ¹ j
	Das reziproke Gitter ist von größter Wichtigkeit, da es für Rechnungen aller Art sehr viel häufiger benötigt wird als das Raumgitter.
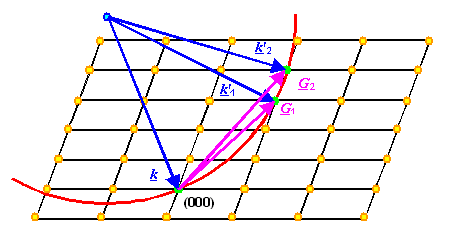
		Es erlaubt aber auch rein geometrische Konstruktionen von Beugungsexperimenten mit großer Aussagekraft. Die gilt insbesondere für die "Ewaldkugel"
		Eine Kugel mit dem einfallenden, mit der Spitze am Nullpunkt des reziproken Gitteres befestigten Wellenvektor als Radius, schneidet "automatisch" alle reziproken Gitterpunkte, deren zugehörige Ebenen den einfallenden Strahl reflektieren, d.h. die Bragg-Bedingung erfüllen.
	Damit lassen sich sehr leicht alle möglichen Fallunterscheidungen "durchdeklinieren"; (z.B. kleine/große Wellenvektoren, monochromatische/polychromatische Wellen, Einkristall/Polykristall; ortsfester/bewegter Kristall; ...); die Ewald Konstruktion ist also sehr hilfreich bei der Visualisierung dessen was passieren kann (und wird).

© H. Föll (MaWi 2 Skript)