3.3.2 Die Ewald Konstruktion der Beugung

	Nachdem wir jetzt das reziproke Gitter verstanden haben, wollen wir es auch benutzen.
		Die erste Anwendung betrifft die sogenannte Ewald Konstruktion der Beugung. Es handelt sich dabei um eine an Einfachheit nicht mehr zu überbietende geometrische Umsetzung der vektoriellen Bragg Bedingung.
	Gegeben sei ein Wellenvektor k und ein Gitter; beide haben eine feste räumliche Orientierung zueinander. Denn obwohl der Wellenvektor die Dimension cm– 1 hat, d.h. im Ortsraum eigentlich gar nicht definiert ist, legt er doch über Amplitude = A(r) = A0 · eikr die Richtung der Welle im Ortsraum eindeutig fest.
		Wir fragen, welche der unendlich vielen Netzebenenscharen des Gitters die Bragg-Bedingung erfüllen.
		Dazu zeichnen wir einfach das reziproke Gitter in der exakten Orientierung relativ zu dem Wellenvektor (beide können in dasselbe KO System eingezeichnet werden, da beide die Maßeinheit m– 1 haben). Die Spitze des Wellenvektors lassen wir auf dem Nullpunkt des reziproken Gitters enden.
		Danach zeichen wir einen Kreis mit Mittelpunkt am Anfangspunkt von k und Länge |k|. Dreidimensional wird das natürlich eine Kugel, die sogenannte Ewald Kugel.
		Das war's. Offenkundig, wie unten zu sehen, erfüllen alle Ebenen, deren reziproke Gitterpunkte von der Ewaldkugel geschnitten werden, die (zweite Variante der) Bragg -Bedingung. (Nicht vergessen: Jeder Punkt im reziproken Gitter steht für eine Ebenenschar des Raumgitters!)
		k' – k  =  G
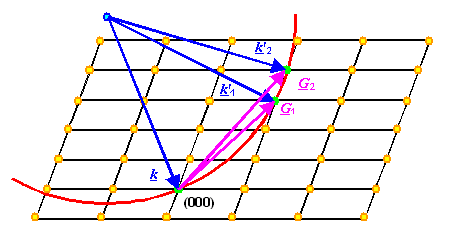
	Die ganze Konstruktion ist unten gezeigt; die möglichen k' Werte sind eingezeichnet.
	Es drängt sich natürlich eine Frage auf: Ein mathematischer Kreis schneidet einen mathematischen Punkt nie, da sowohl Linie als auch Punkt unendlich "dünn" sind.
		Was also heißt "...geschnitten werden..." in unserem Fall? Einfach nur, daß Ewald Kugel und reziproker Gitterpunkt sich nahe genug kommen.
		Aha! Und was heißt nahe genug? Nun ja, eine echte Welle hat nie eine exakte Wellenlänge, sondern eine bestimmte Frequenz- und Wellenlängenverteilung, und damit auch einen k-Vektor mit einer gewissen Längenverteilung Dk. Unsere Kreislinie ist also keine Linie, sondern ein dünnes Band - und damit kann man einen Punkt schon "schneiden".
		Außerdem sind unsere reziproken Gitterpunkte bei echten Kristallen auch keine mathematischen Punkte, sondern haben eine endliche Ausdehnung, die proportional zu den reziproken Dimensionen des realen Kristalls sind. Nur ¥ große Kristalle haben ¥ kleine reziproke Gitterpunkte.
	Damit kann man, wenn man will (und kann) "nahe genug" beliebig genau quantifizieren. Wir wollen (und können) das aber nicht - glauben es aber trotzdem.
	Man kann die Ewald Konstruktion natürlich sofort erweitern und zum Beispiel untersuchen:
		Was passiert, wenn die einfallende Welle nicht monochromatisch ist, sondern einen bestimmten Bereich an Wellenlängen abdeckt? Klar: Viele Kugeln einzeichnen (ein Kontinuum); eine trifft einen gegeben Punkt des reziproken Gitters immer, wir bekommen Reflexe von (fast) allen Ebenen.
		Was passiert, wenn die einfallende Welle monochromatisch ist, wir aber den Kristall drehen. Klar: Bei einem definierten Drehwinkel wird ein herausgegriffener Punkt des reziproken Gitters "reflektieren", d.h. die Ewald Kugel schneiden.
	Damit sind wichtige Methoden zur Strukturuntersuchung schon angedeutet, wir werden darauf später noch näher eingehen.

© H. Föll (MaWi 2 Skript)