Interferenz und Beugung

	Interferenz und Beugung sind die beiden Schlagwörter, die man klassisch nur mit Wellen assoziiert.
		Interferenz ist das Fundamentalphänomen; Beugung ist ein Konsequenz der Interferenz, in der Regel benutzt man diesen Begriff falls Wellen mit periodischen Strukturen wechselwirken.
	Interferenz heißt schlicht, daß bei der direkten Überlagerung von Wellen sich die Amplituden nicht einfach addieren, sondern je nach Phasenbeziehung verstärken oder schwächen können.
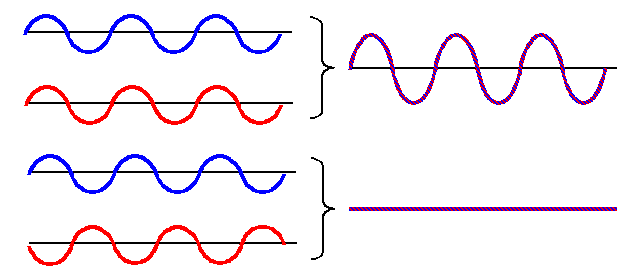
		Das kann bis zur totalen Auslöschung führen, falls eine Phasenverschiebung von genau 180o (oder p) vorliegt. Jeder kennt die simplen Bildchen dazu:
		Zwei Wellen gleicher Frequenz, die in dieselbe Richtung laufen, können sich zu einer Welle doppelter Amplitude verstärken oder komplett auslöschen - auch konstruktive oder destruktive Interferenz genannt.
		Zwei klassische Teilchen gleichen Impulses tun das nie, sie laufen einfach nebeneinander her.
	Weniger bekannt ist schon, was passiert wenn viele Wellen mit allen möglichen Phasen miteinander interferieren. In der Antwort auf dieser Frage steckt nicht nur (mindesten) die halbe Quantentheorie (in der Feynmanschen Formulierung), sondern auch so simple Dinge wie das Reflektionsgesetz: "Einfallswinkel = Ausfallswinkel". Schauen wir uns das einmal in einer speziellen und idealisierten Version an.
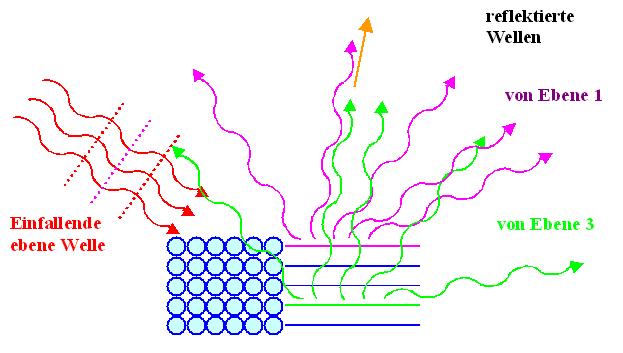
		Wir lassen eine (ebene) Welle auf ein reflektierendes Material fallen. Da wir auf der Ebene der Atome schauen wollen, nehmen wir einen Idealkristall wie unten gezeigt.
		Die einfallende Welle kennt das Reflektionsgesetz (noch) nicht, wir nehmen ganz allgemein einfach mal an, daß ein Teil von ihr an jeder Atomlage in alle möglichen Richtungen reflektiert wird - das sieht dann so aus
		Um Zeichenarbeit zu sparen, sind im rechten Teil nur noch die Ebenen auf den Atome sitzen angegeben und ein paar der möglichen Wellen gezeigt, die unter beliebigen Winkeln and der ersten und dritten Ebene reflektiert werden. Alle andere Ebenen machen genau dasselbe, aber das Bild wird zu unübersichtlich, wenn man das alles einzeichnet.
	Wie groß ist jetzt die Intensität der gesamtem reflektierten Welle in eine ganz bestimmte, willkürlich herausgegriffene Richtung?
		Um das herauszufinden müssen wir nur alle Wellen, die von allen beteiligten Ebenen in diese Richtung reflektiert werden, aufaddieren - aber phasenrichtig, d.h. unter Berücksichtigung von Interferenz.
		Greifen wir beispielsweise die orange eingezeichnete Richtung heraus, sehen wir, daß schon die beiden eingezeichneten Teilwellen, die in diese Richtung laufen, verschiedene Phasen haben.
		Betrachten wir alle Teilwellen in diese Richtung, finden wir alle möglichen Phasen. Addieren wir alle auf, ist das Resultat = 0 !!!!. Denn zu jeder Welle mit irgendeiner Phase, findet sich eine andere mit genau entgegengesetzter Phase (¥ viel Wellen, oder zumindest sehr viele, vorausgesetzt).
	Nur für eine Richtung haben alle Wellen genau die gleiche Phase - und das ist, wenn man das ganze analysiert, die Richtung für die Ausfallswinkel = Einfallswinkel gilt (falls auch der Abstand der Atome noch "stimmt"; aber das ist eine Komplikation, die uns hier nicht beschäftigen soll).
		Was wir hier betrachtet haben, ist nichts weniger als die Beugung von Wellen an einer periodischen Struktur (am Beispiel war es eine dreidimensionale periodische Anordnung von Atomen - ein Kristall); alle Beugungseffekte resultieren aus der Interferenz der beteiligten Wellen.
		Für Lichtwellen hätten wir übrigens nicht in Dimensionen von Atomen schauen müssen - Dimensionen in der Größenordnung der Wellenlänge (d.h. ungefähr im µm Bereich) hätten genügt. Aber die Betrachtung gibt exakt das wieder was einem Elektronenstrahl (mit viel kleinerer de Broglie Wellenlänge) widerfährt, wenn er auf eine realen Kristall trifft: Er wird gebeugt - wie eine Welle!
	Das "paradigmatische" Experiment zu Interferenz und Beugung ist natürlich das Youngsche Experiment der Beugung am Doppelspalt.
		Macht man das mit Licht, nimmt man an, daß von den (kleinen) Spalten jeweils ein Zylinderwelle ausgeht; die Interferenz der beiden Zylinderwellen gibt das bekannte Streifenmuster auf einem Bildschirm hinter der Anordnung:
		0
		Hier eine besonders hübsche alte graphische Darstellung, erhalten durch die Überlagerung von Kreisen ausgehend von den beiden Spalten S1 und S2
	Und genau so sieht nicht nur die Intensitätsverteilung für Lichtwellen aus, sondern auch die Aufenthaltswahrscheinlichkeit |y|2 für einen Elektronenstrahl.
		Dabei ist das eigentliche Mysterium, daß hier nicht zwei Elektronen "irgendwie" miteinander interferieren (ein gerne gemachter Gedankenfehler), sonder ein Elektron mit sich selbst!
		Zum Schluß noch ein richtiges Beugungsbild, wie man es von einem Elektronenstrahl erhält, der auf einen Kristall fällt (und in diesem Fall auf der anderen Seite wieder herauskommt).
		Die Probe war in diesem Fall eine Schichtung von drei sehr dünnen kristallinen Folien (Si, NiSi, und Ni2Si); der Elektronenstrahl kommt, wenn man so will, senkrecht zum Bildschim von hinten.
		Die exakte kristalline Struktur aller drei Materialien fndet sich wieder in dem typischen Interferenzmuster, bestehend aus (mehr oder weniger scharf) definierten Beugungspunkten.

Mit Frame

2.1.2 Fruehe Atommodelle: Bohr und de Broglie

Richard Feynman

© H. Föll (MaWi 1 Skript)