 |
For a given lattice, there is a simple way of constructing an unique elementary
cell, avoiding all the difficulties with primitive and non primitive elementary cells, Bravais lattices that show all the
symmetry or only parts, and so on. |
|
 |
The catch is, you may loose everything that makes a lattice special. The resulting
elementary cells may appear downright ugly. |
|
 |
That's why they are rarely used as long as we look at crystal lattices in normal space. But
whenever we consider electronic properties, we will construct lattices in some other
space - in particular wave vector or momentum space - and that's when we use Wigner - Seitz cells,
as they are called, exclusively. |
 |
Well - here is the recipe: |
|
 |
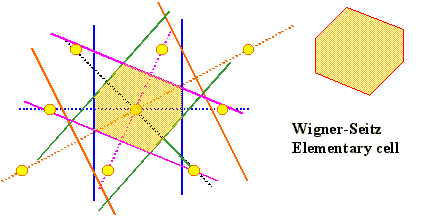
Choose a zero point of your lattice. |
|
 |
Draw lines from your zero point to all neighboring lattice points; take as many as you want
- nearest neighbors, second-nearest neighbors, etc. |
|
 |
Draw a plane (two-dimensional a line), that exactly bisects all of your lines at a right angle. |
 |
That's it. A subset of all your planes will form some closed body, and that is
your Wigner Seitz elementary cell, That it is an EZ is easy to see: just repeat it all over space - it will produce
your crystal if you put your base - the atoms - at the right positions inside your Wigner-Seitz EZ. |
|
 |
Below it is done for a two-dimensional lattice. |
| |
|
© H. Föll (MaWi 1 Skript)
![]() 3.1.2 Kristall = Gitter + Basis
3.1.2 Kristall = Gitter + Basis