 |
Die Stirlingsche Formel ist ein unverzichtbares Hilfsmittel bei allen kombinatorischen
und statistischen Formeln; sie ermöglicht mit Fakultäten
einfach zu rechnen. |
|
Sie existiert in mehreren Versionen, die verschiedene Genauigkeitsgrade
darstellen. Sie ist relativ leicht in einfacher Form ableitbar: |
|
 |
Es ist |
| |
| ln x! = | ln 1 + ln 2 + ln 3 + .... + ln x |
|
|
|
|
mit y = die ganzen positive Zahlen beginnend bei 1. |
|
Für große y kann man statt der Summe näherungsweise ein Integral nehmen,
es gilt ln y »
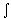 ln y · dy (von 1 bis x). Es gilt |
|
|
x
S
1 | ln y » |
x
ó
õ
1 | ln y · dy |
x
ó
õ
1 | ln y · dy | = |
y · ln y – y |
|
|
|
|
Nach Einsetzen der Integrationsgrenzen erhält man |
|
|
| ln x! » | x
ó
õ
1 | ln y · dy |
= | y · ln y – y | x
ç
ç
1 |
= |
x · ln x – x + 1 |
|
|
|
Das ist die einfache und leicht zu verstehende
Version der Stirlingformel. |
|
|
Für sehr große x kann man auch noch den Term x + 1 gegenüber
x · ln x vernachlässigen und erhält die ganz simple und in der Regel verwendeteVersion |
| |
|
|
Damit hat man aber nicht nur eine numerische Näherung genacht, sondern aus einer diskreten Funktion, die nur für ganze positive Zahlen
definiert ist und als Ergebis auch immer nur ganze positive Zahlen haben kann, eine kontinuierliche
Funktion gemacht, die für alle Zahlen ausgerechnet werden kann, wobei aber offen
bleibt, was der Wert für z.B. 3,73! bedeutet. |
|
|
Das hat Konsequenzen, z.B. den bei der Herleitung der Gaußverteilung verbundenen Übergang von absolutenWahrscheinlichkeiten
zu Wahrscheinlichkeitsdichten. |
|
Eine noch genauere Näherung, die aber nicht mehr leicht herleitbar ist und schon für
x £ 10 ganz gut ist, gibt die folgende Version der Stirlingschen Formel |
| |
| ln x! » |
ln (2p1/2) + (x + 1/2) · ln (x) – x
|
|
|
© H. Föll (MaWi 1 Skript)
Kurzfassung der Ableitung der Gauss Verteilung 
Mit Frame