Binomialkoeffizient

	Der Binomialkoeffizient kommt in vielen mathematischen Formeln vor, insbesondere in der Stochastik, so dass er einen eigenen Namen und eine eigene Abkürzungen bekommen hat
		Der Binomialkoeffizient zweier (ganzer und nicht negativer) Zahlen N und n ist wie folgt definiert
		æ è N k ö ø  =  Binomial Koefficient  =  N! (N – k)! · k!
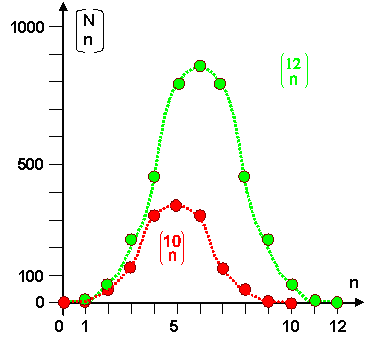
	Wie sieht ein zugehöriger Graph aus? Etwa so:
		Man erhält immer eine Art Glockenkurve, mit dem Maximum bei n = N/2.
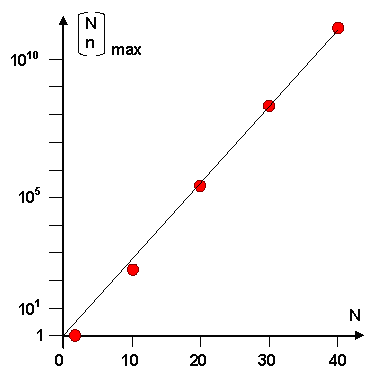
		Das Maximum wächst sehr rasch, nämlich exponential für nicht zu kleine N, wie im linken Graph gezeigt.
	Mit Hilfe der Stirlingformel kann man den Binomialkoeffizient etwas zu Leibe rücken und findet dann schlicht und wohl nicht ganz überraschend:
		Um das Maximum herum erhalten wir schlicht die Gauss-Verteilung.

Mit Frame

Ableitung der Gauss Verteilung

Combinatorics

Stirlingsche Formel

© H. Föll (MaWi 1 Skript)