9.2.4 Gummielastizität

Mechanismus

	Gummielastizität, es wurde schon mehrmals betont, ist etwas Besonderes.
		Sobald wir ein Elastomer auf die doppelte und dreifache Länge ausziehen, müssen wir nicht Arbeit leisten weil wir die elastische Energie des Materials erhöhen, sondern weil wir die Entropie der Konformation erniedrigen.
		Schauen wir uns das im Modell an:
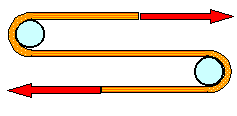
		Ein Stück Gummi; wir beginnen daran zu ziehen.		Es ist ziemlich lang geworden
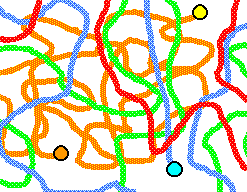
		Die Ketten im unbelasteten Zustand sind wirr gefaltet; sie laufen willkürlich durcheinander, sie sind rein statistisch angeordnet.		Die Ketten im belasteten Zustand sind alle ziemlich langgestreckt. Einige Vernetzungen (schwarz) sind angedeutet.
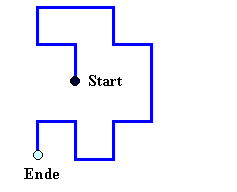
		Das Molekül im Model des unbelasteten Zustands. Nach jedem C-Atom kann die Kette nach oben, unten oder nach links/rechts weitergehen Welche der immer drei Möglichkeiten jeweils vorliegt ist "rein statistisch".		Das Molekül im Model des belasteten Zustands. Nach jedem C-Atom kann die Kette nach oben, unten oder nach links/rechts weitergehen. Sie wird aber meisten nach rechts (in Zugrichtung) fortgesetzt - die drei Möglichkeiten sind nicht mehr statistisch verteilt.
	Das Grundprinzip der Dehnung ist klar: Ketten werden reversibel gestreckt. Ob der höhere Grad der Ausrichtung sich nach jedem C-Atom durchsetzt, oder nur auf größeren Skalen, ist zunächst egal.
		Was ist der Unterschied im Zustand, im thermodynamischen Potential des gedehnten und ungedehnten Gummis? Dazu müssen wir die freie Enthalpie der beiden Zustände betrachten. Wir machen das mal parallel für den ungedehnten und den gedehnten Zustand.
		Ungedehnt		Gedehnt
		Gu= Hu – TSu = UB – TSu		Gg= Hg – TSg = UB – TSg
		UB ist die Bindungsenergie - in beiden Fällen. Denn der Enthalpieterm enthält im wesentlichen die innere Energie U, und die ist durch die Bindungen und sonst nichts gegeben.
		Der entscheidende Punkt ist, daß im ungedehnten und gedehnten Zustand die Bindungsenergien identisch sind. Denn sowohl die Bindungsabstände als auch die Bindungswinkel, die alleine die Bindungsenergie bestimmen, sind gleich - nur die Verteilung der Bindungswinkel ist anders.
	Das gilt aber nicht für die Entropie! Der gedehnte Zustand ist eindeutig ordentlicher, hat also die kleinere Entropie. Damit wird Gg größer - im gedehnten Zustand steckt die Energie .
		DG  =  Gg– Gu =  T· (Su – Sg)
		Um vom Zustand "u" zum Zustand "g" zu kommen, muß also Arbeit verrichtet werden - wir müssen eine Kraft F anwenden, die in Richtung der Dehnung mit dem Weg l die notwendig Arbeit DG leisten kann. Diese Arbeit ist dann.
		DG =  lg ó õ lu F· dl
		Dabei muß die insgesamt geleistete Arbeit von Weg unabhängig sein, es gilt also in differentieller Form F=¶G/¶l .
		Hier steckt ein tiefes Prinzip: Die Ableitung eines thermodynamischen Potentials nach dem Weg ergibt genauso eine Kraft wie die Ableitung eines rein mechanischen Potentials. Im übrigen müssen wir, falls wir Dehnungen e benutzen, für die bei Elastomeren möglichen großen Verformungen unbedingt die sog. wahren Dehnungen benutzen. Das ist aber für das folgende nicht so wichtig.
	Entscheidend für die Gummielastizität ist also die Entropie des Materials und ihre Änderung im Zugversuch. Das Elastomer hat einen endlichen E-Modul, weil es sich beim Langziehen gegen die damit verbundene Verringerung der Entropie "wehrt".
		Im folgenden werden wir eine sehr einfache Formel für den E-Modul von Elastomeren ableiten, die vollständig auf der statistischen Definition der Entropie beruht. Während das Ergebnis sehr einfach ist, hat die Herleitung allerdings viele Tücken, denen wir aber durch kleine Tricks aus dem Wege gehen werden.
		Es ist aber zum Verständnis der Entropie sehr nützlich, sich die Gummielastizität doch einigermaßen gründlich anzusehen.

	Die Entropie der Konformation und die notwendige Kraft für Dehnung
	Die zum thermodynamischem Gleichgewicht gehörende maximale Entropie einer Polymerkette die in der Konformation der Kette, also der räumliche Anordnung steckt, ist dann erreicht, wenn größtmögliche Unordnung vorliegt.
		Für jede beliebige Einzelkette bedeutet dies, daß beim Aufbau der Kette jede der Möglichkeiten das nächste Kettenglied "anzudocken" mit gleicher Wahrscheinlichkeit vorliegt.
		In anderen Worten: Falls in einem idealisierten zweidimensionalen Modell wie oben gezeigt, das nächste Monomer immer drei Möglichkeiten der Ankopplung hat, werden wir im thermodynamischen Gleichgewicht, also bei einem Polymer das unbelastet "nur so rumliegt" alle drei Möglichkeiten mit gleicher Häufigkeit finden.
	Diese Definition der Kettenkonformation ist aber nichts anderes als die Definition eines "Random Walks". Damit können wir sofort drei Konformationsparameter für den Zustand "u"(=unverformt=maximale Entropie sofern Gleichgewicht vorliegt) quantifizieren:
		1. Der mittlere Abstand <r> zwischen dem Beginn und dem Ende einer Kette, die aus N Kettengliedern der Länge a0 besteht. Das ist genau die in Kapitel 6.3 eingeführte Diffusionslänge, denn die Abfolge der Kettenglieder entspricht genau einem "random walk" mit Schrittweite a0 und N Schritten. Wir haben also
		<r>=r0 =  a0 · (3N)½
		2. Der maximale Abstand oder die maximale Kettenlänge rmax; er liegt vor bei vollständig gestreckter Kette und wir haben
		rmax =  a0· N
		3. Die Verteilung der Abstände. Aus allgemeinen mathematischen Kenntnissen wissen wir, daß die Verteilung von Zufallsgrößen um ihren Mittelwert meistens durch eine Gauß-Verteilung gegeben ist. Und aus der detaillierten Analyse des "random walks" in einem "advanced" Modul , entnehmen wir die hier passende Formel:
		Die Wahrscheinlichkeit w(r)DV, daß das Ende der (am Nullpunkt beginnenden) Kette im Volumenelement DV=DxDyDz bei (x, y, z) liegt ist
		w(x,y,z)DV  =  æ è 1 2pNa02 ö ø 3/2 · exp – x2 + y2 + z2  2Na02   · DV  =  æ è 1 2pNa02 ö ø 3/2 · exp – r2  2Na02    · DV
		Denn x2 + y2 + z2=r2 gilt natürlich immer.
		Das ist aber nicht wie sonst so oft die Wahrscheinlichkeit, das Kettenende irgendwo im Abstand r zu finden, d.h. nicht die Wahrscheinlichkeit, daß die Kette irgendwo in der "Zwiebelschale" zwischen r  und r + Dr  endet. Wir sind immer noch im Volumenelement bei (x, y, z). Konfusion an diesem Punkt ist ein beliebter Fehler - z.B. im "Gerthsen".
	Allerdings haben wir jetzt ein bißchen gemogelt: Ein "Spaziergang" entlang der Kette ist nicht exakt ein "random walk", weil alle Schritte, die uns an einen Ort bringen, an dem wir schon mal waren, verboten sind.
		Denn das würde bedeuten, daß zwei Kohlenstoffatome am selben Platz sitzen, die Kette sich also auf sich selbst legt - und das müssen wir ausschließen.
		Was folgt, ist also bis zu einem gewissen Grad eine Näherung. Es ist aber (hoffentlich) einsichtig, daß die grundsätzlichen Folgerungen, die wir in diesem Kapitel ziehen, davon nicht betroffen sind.
	Die Entropie einer Kohlenstoffkette ist nun direkt und ohne Umschweife
		S =  k · ln [w(x,y,z) · DV]
		Denn genauso hatten wir die Entropie definiert: k · ln aus der Wahrscheinlichkeit des Auftretens eines Makrozustandes. Und die hier in Frage kommenden Makrozustände sind definiert durch die Koordinaten (nicht des Abstands) des Kettenanfangs und Kettenende. Nebenbei: w(x,y,z) ist eine Wahrscheilichkeitsdichte; wir müssen also mit DV multiplizieren, um eine absolute Wahrscheinlichkeit ohne Dimension zu erhalten.
		Warum? Warum nehmen wir als Makrozustand nicht einfach den Abstand zwischen Kettenanfang und Kettenende? Eine berechtigte Frage, die wir hier aber nicht vertiefen wollen. (Das bedeutet, so klar ist die Antwort auch nicht, bzw. wer weiß das schon.)
	Jetzt können wir die Kraft F berechnen, die erforderlich ist, um vom ungedehnten Zustand die Kette um ein Stückchen dr zu verlängern.
		Nach den weiter oben bereits angestellten Überlegungen gilt
		F  =  ¶ G ¶l  =  – T · ¶S(r) ¶r
		Damit bekommen wir
		F  =  – k ·T · ¶ ¶r  æ è ln (const.)   –    r2  2Na02 ö ø  =  k · T · r  Na02
	Das ist schon ein bemerkenswertes Ergebnis! Die Kraft, mit der sich ein Stück Gummi gegen Verformung wehrt, steigt mit der Temperatur und ist proportional zu r und damit "irgendwie" auch zur Dehnung e.
		Bevor wir aber hier weiter philosophieren, machen wir noch einen weiteren Schritt. Wir können für Na0 die maximale Kettenlänge rmax einsetzen und erhalten
		F =  kT  a0   ·  r  rmax

Vernetzung und E-Modul

	Was bestimmt rmax, die maximale Kettenlänge? Galaktisch gesehen natürlich das Ausgangspolymer - aber man kann das noch ein bißchen enger sehen!
		Dazu schauen wir uns jetzt eine Graphik an, die den gedehnten Zustand besser wieder gibt als das simple Bildchen von weiter oben:
		Gezeigt ist die extreme Situtation einer sehr hohen Vernetzung, das Polymer ist eher ein Duroplast als ein Elastomer. Die aber auch für reguläre Elastomere geltenden Punkte sind besser zu sehen.
	Wir erkennen die folgenden "feinen" Punkte:
	1. Wir haben die Vernetzung übertrieben, aber realistischer eingezeichnet als ganz oben. Die Struktur ähnelt mehr einem Netzwerk als einem Spaghettiball.
		Das muß sie auch, denn ohne einen relativ hohen Grad an Vernetzung ist das Phänomen der Gummielastizität nicht sehr ausgeprägt.
		Diese Behauptung wird sich gleich in einer Formel wiederspiegeln.
	2. Unsere Betrachtung hat nicht berücksichtigt, daß wir nur in eine Richtung ziehen. Was wir aber bisher betrachtet haben, war sozusagen "allseitiger Zug" - aus einer kleinen Gummikugel wird eine große.
		Bei einachsigem Zug haben wir aber nicht nur erhebliche Querkontraktion, es wird auch offenbar nur ein Teil (etwa 1/3) der Ketten langgezogen - die Ketten quer zur Zugrichtung werden eher gestaucht. Das ändert zwar auch die Entropie, aber in vermutlich etwas anderer Weise als bisher betrachtet. In unserer Rechnung ist das nicht berücksichigt.
	3. Die maximale Länge der gedehnten Ketten ist jetzt im wesentlichen durch die Vernetzung sowohl begrenzt als auch indirekt festgelegt.
		Im Gleichgewicht, d.h. im linken Bild, muß der Abstand rK zwischen den Vernetzungsknoten gleich dem mittleren Abstand r0 zwischen den Enden der Ketten sein. Das sieht man dem Bild nicht so direkt an, aber man muß sich das ganze dreidimensional vorstellen, dann wird es etwas einsichtiger.
		Mit einer Knotendichte rK und dem daraus folgenden mittleren Abstand zwischen den Knoten
		rK  =   æ è 1  rK ö ø 1/3  =   1  rK1/3   :=  r0  = a0 · (3N)1/2
		erhalten wir die Beziehung
		1 rK2/3  =  3 · rmax · a0 rmax =  1 3 · a0· rK2/3
	Eingesetzt in den Ausdruck für die Kraft erhalten wir ein im Wortsinn spannendes erstes Endergebnis:
		F =  kT  a0   ·  r  rmax  =  r · kT · (3a0 · rK2/3) a0  =  3kT · rK2/3 · r
		Die Kraft, mit der ein Elastomer zurückzieht, ist also proportional zum Auszug r, zur Temperatur T und etwas schwächer als linear zur Knotendichte. Wir können das noch etwas eleganter ausdrücken, indem wir jetzt den E - Modul berechnen
	Der Elastizitätsmodul E war definiert als
		E =  ds de
		Wie schon bei der Ableitung des E-Moduls aus den Bindungspotentialen rechnen wir um in Kräfte F und Abstände r über
		s =  F   r02 e =  r – r0 r0 ;     daraus     de dr  =  1  r0
		Dabei ist zu beachten, daß die Fläche, auf der die Kraft F angreift, der Projektionsfläche einer "geknäuelten" Kette entspricht, die wir einfach mit r02 grob nähern. Damit bekommen wir
		E=   ds de  =  1  r02  ·  dF dr  ·   dr de  =  r0 r02   ·  dF dr  =  1  r0  ·   3k ·T · rK2/3
		Nun ist aber r0 nichts anderes als 1/rK1/3 und wir bekommen
		E   »  3kT · rK
		- ein monumental einfaches Ergebnis! Der E-Modul eines Elastomers ist nur eine Funktion der Knotendichte und der Temperatur! Die "Chemie" kommt gar nicht vor!
	Und daran wird sich nicht viel ändern, falls wir jezt mit wesentlich komplizierteren Betrachtungen versuchen, der Fragestellung gerechter zu werden. Im wesentlichen ändert sich der Faktor 3, aber die funktionalen Abhängigkeiten bleiben im wesentlichen erhalten. Man erhält beispielsweise bei Berücksichtigung von Querkontraktion und einachsigem Zug (nachzulesen im Gerthsen)
		E =  3 2 kT · rK
	Wie gut ist diese Formel? Nehmen wir Raumtemperatur, d.h. kT » 1/40 eV (eine Zahl, die man kennen sollte) oder kT = 0,025 · 1,6 · 10–19 J = 4 · 10–21 J und eine Knotendichte von einem Knoten alle 100 nm (also nach ca. 300 Kettengliedern), d.h. rK = 1/(100 nm)3 = 10–6 nm–3 = 1021 m–3
		Damit haben wir einen E-Modul von E = 1,5 · 4 · 10–21 · 1021 Jm–3 = 6 Pa
		Das liegt genau im unteren Bereich der Elastomere wie in den früheren Graphiken gezeigt. Wir liegen also nicht schlecht mit der Theorie.
		??????? Big mistake! Nobody noticed but J.-M. Wagner in 2024
		Wir erhalten ungefähr 1 Pa. Die Einheiten in den Bildern sind aber MPa! Wir liegen um einen Faktor 106 daneben!
	Ein Rätsel. Die Formel ist im Prinzip richtig, seriöse Bücher kommen zum prinzipiell gleichen Ergebnis (hier ist ein Beispiel).
		Was ist schiefgelaufen? Das wird weiter unten erklärt; zunächst aber noch die alten Schlußfolgerungen, die immer noch gelten.
	Was haben wir gelernt? Sehr viel:
		1. Entropie ist sehr real! Es ist die Entropie, die zurückzieht, wann immer wir Elastomere verformen.
		2. Der statistische Zugang zur Entropie mag mühsam sein – aber er trägt sehr weit. Es gibt keine andere Möglichkeit, ein so fundamentales Materialphänomen wie die Gummielastizität anders zu verstehen oder einfacher in Formeln zu gießen.
		3. Die Beziehungen rund um den "Random walk" sind wichtig! Sie werden uns in anderen Zusammenhängen noch oft begegnen – zum Beispiel in den Strom-Spannungs-Kurven von Halbleiterbauelementen.
		4. Wir haben die Gummielastizität nicht nur quantitativ verstanden – unsere einfache Formel hat die wesentlichen Beobachtungen gut eingefangen –, sondern wir wissen im Prinzip auch, was man tun muß, um die Gummielastizität (und damit indirekt auch das Verhalten mancher Biomaterialien) im Detail zu verstehen.

	Der Fehler
	Wir haben schlicht und ergreifend eine völlig falsche Zahl für die Knotendichte benutzt: Wir haben einen Knoten alle 100 nm angenommen, und dann die Dichte als 1/(100 nm)3 definiert.
		Das bedeutet, dass wir unser Polymer als kubische Struktur mit den Ketten als 100 nm lange Seiten eines Würfels auffassen. Das Polymer bestünde dann im wesentlichen aus leerem Raum.
		In der Realität sind die Ketten aber nicht gerade, und wir habe eine Art von dichter Packung der Ketten: Zu einem Knoten gehören drei Ketten (jede Kette gehört zu 4 Würfeln), und diese Ketten nehmen bei dichter Packung ein Volumen von 3 mal Kettenlänge rK mal Kettenquerschnittsfläche a2 ein.
		Nehmen wir der Einfachheit halber die Kettenquerschnittsfläche als 1 nm2, befindet sich ein Knoten in einem Volumen von 3 rK nm2 statt, wie oben angenommen, in rK3. Die Knotendichte wird damit um einen Faktor rK3 / (3 rK nm2) = 1/3 rk2/nm2 = 1/3 104 größer.
	Damit kommen wir den experimentellen Werten schon viel näher. Da im Realfall die Knotendichte eher höher liegt und unsere Rechnung viele Näherungen enthält, wollen wir uns damit zufriedengeben.
		Wer es genauer wissen will, muss ziemlich viel mathematischen Aufwand treiben.

© H. Föll (MaWi 1 Skript)