|
Ein
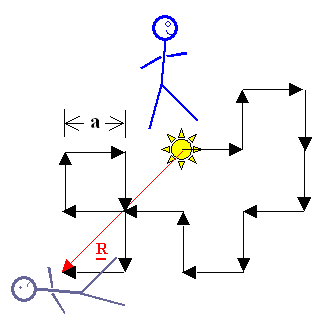
paradigmatischer Volltrunkener kommt aus einer Kneipe
und torkelt durch die Gegend. Jeder Schritt führt mit gleicher Wahrscheinlickeit nach vorne oder hinten, nach rechts
oder links. In welchem mittleren Abstand
<|r|> von der Kneipe finden wir die hilflose
Person nach N Schritten der (immer gleichen) Schrittlänge a? |
| |
|
|
 |
Die Art der Fragestellung ist sehr wichtig. Wir können mehrere Fragen stellen, zum Beispiel: |
|
|
| |
- In welchem mittleren Abstand
<|r|> = <(x2
+ y2)1/2> finden wir die hilflose Person? (die Frage von
oben)
- Wo, d.h bei welchem Ort
r = (x, y) finden wir die hilflose Person?
- Bei welchem Abstand |r|wahr ist es am wahrscheinlichsten,
den Trunkenbold zu finden? 1)
|
|
 |
Die Antworten auf diese drei Fragen können sehr verschieden ausfallen; mehr dazu im mehreren
"advanced" Modulen. |
|
 |
Wir interessieren uns hier primär für den mittleren Abstand.
Offenbar hängt er von der Gesamtzahl der Schritte ab (im Bild sind es 16). |
|
|
| | |
|
 |
In dem obigen Beispiel betrachten wir einen speziellen Fall des sogenannten Random Walk: Zwei Dimensionen, feste
Schrittweite, 4 feste Winkel. Auf deutsch heißt "Random
Walk" "statistische Wanderung" oder Zufallsbewegung- aber
nur der englische Ausdruck ist wirklich geläufig. |
|
 |
Wir werden die noch zu findende Beziehung zwischen dem mittleren Abstand und
der Zahl der Schritte noch öfters brauchen, es lohnt sich also etwas Zeit darauf zu verwenden. Da das Ergebnis aber
recht einfach ist, wollen wir hier nur die Andeutung einer sauberen Ableitung geben,
eine genaue (und unerwartet komplexe) Ausführung findet sich in einem Link. |
 |
Betrachten wir zunächst den allereinfachsten Fall der eindimensionalen
Zufallsbewegung. Unser Teilchen hat dann nur die Möglichkeit, einen Schritt nach links oder nach rechts auszuführen.
|
|
 |
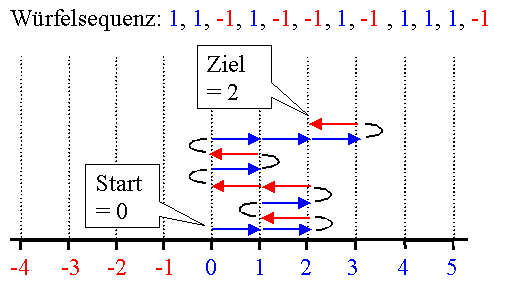
Wir können ein einfaches Experiment durchführen, indem wir eine Münze werfen,
und unser Teilchen bei "Zahl" nach rechts, bei "Kopf" nach links um eine Einheit (unsere Gitterkonstante)
bewegen. Das sieht dann beispielsweise so aus: |
|
|
|
|
 |
Das läßt sich auch relativ leicht simulieren, ein entsprechendes "Experiment"
(bei dem der Computer per Zufallsgenerator würfelt) ist in einem Link dargestellt. Es lohnt sich, ein bißchen
zu spielen. |
| |
Link
zum "Random Walk"
Simulator
|
|
 |
Spielt man ein bißchen mit dem Simulator, oder wirft selbst eine Münze,
fällt schnell auf, daß ein Teilchen nach einigen Würfen in der Regel nicht mehr beim Ausgangspunkt ist,
obwohl die Wahrscheinlichkeiten für Schritte nach rechts oder nach links genau gleich groß sind. |
|
 |
Das kann man etwas genauer betrachten. Nehmen wir nicht eine Münze, sondern
einen (fiktiven) Würfel mit nur zwei Zahlen – 1 und + 1, brauchen wir nur die Summe der Augen nach
N Würfen zu betrachten. Ist sie 0, dann ist das Teilchen wieder am Ausgangsort, ist sie beispielsweise
+ 5 oder – 8, dann ist das Teilchen 5 Schrittlängen nach rechts oder 8 Schrittlängen
nach links gewandert. Ist die Summe +N oder –N, ist der jeweilige Maximalwert erreicht;
ein ziemlich unwahrscheinliches Ereignis. |
|
 |
Wir können offenkundig dasselbe Ergebnis
erhalten, wenn wir nicht mit einem digitalen Würfel (Augenzahlen sind + 1
und – 1) N mal würfeln, sondern N digitale Würfel gleichzeitig
werfen. Auch dann ist nur die Summe der Augenzahlen entscheidend für die Endposition. |
 |
Die Wahrscheinlichkeit wN(x), mit N
Würfeln, die alle digital sind, d. h. nur + 1 oder – 1 als Augenzahl haben, mit einem
Wurf eine Summe x zwischen – N und + N zu würfeln, ist dann in Prosa
leicht zu definieren; |
|
 |
wN(x) = (Zahl der Möglichkeiten x
zu würfeln)/(Zahl aller möglichen Wurfergebnisse). |
|
 |
Das erinnert uns an die Definition
der Entropie. |
 |
Offensichtlich läßt sich unsere Eingangsfrage
in ein Würfelspiel "übersetzen", und dann mit den Regeln der Kombinatorik und Wahrscheinlichkeitsrechnung
beantworten. Wie angekündigt, wollen wir hier aber nicht weiter die mathematische Ableitung der Formel für wN(x)
verfolgen; das wird im Link getan. |
|
 |
Anmerken kann man aber, daß in der sauberen Ableitung der gesuchten Formel die Gauss-Verteilung
auftaucht; und daß die korrekte Ableitung trotz der einfachen Ausgangsfragestellung zahlreiche Tücken hat (in
allen Auflagen des "Atkins", der als eines
der wenigen Bücher dies überhaupt tut, sind z.B. Fehler; siehe obigen Link). |
|
 |
Wir wollen deshalb zur Ableitung des mittleren Abstands
zwischen Start und Ziel nach N Schritten mit der Schrittweite a in der eindimensionalen
Diffusion eine der trickreichen Schnellableitungen benutzen, die Richard Feynman
für viele Formeln in seinen "Lectures" gegeben
hat. |
| |
|
|
Schnellableitung des Ergebnisses |
| |
|
 |
Wir bezeichnen den Abstand zwischen Startpunkt und der jeweiligen Position mit
dem (eindimensionalen) Vektor R. Ein einzelner Schritt sei durch
einen eindimensionalen) Vektor a gegeben; für eindimensionalen
random walk in einem Gitter hätte a dann nur die Werte ±|a|. |
|
 |
Die Schlüsselfrage ist: Wie groß ist der Betrag
von R = |R| = R nach N Schritten? |
|
 |
Gleichbedeutend und einfacher ausrechenbar ist die Frage nach dem mittleren
Abstandsquadrat, <R2>,
das nach N Schritten vorliegt, da gilt |
|
|
|
|
 |
Dazu betrachten wir die Lage zu irgendeinem Zeitpunkt, z.B. nach N – 1
Schritten; der Abstand ist dann RN – 1. |
|
 |
Der nächste Schritt wird den Vektor a
addieren; wir landen bei |
|
|
|
|
 |
Wir bilden nun RN2 : |
| |
| RN2 = |RN|2
= | æ
è |
RN – 1 + a |
ö
ø | 2 |
= |
(R2N – 1) + 2 · a · RN
– 1 + a2 |
|
|
|
 |
Davon wollen wir den Mittelwert, d.h. wir müssen
über viele RN2 mitteln. Da dabei a richtungsmäßig
alle möglichen Werte haben kann; wird +a genauso häufig vorkommen wie –a;
der Mittelwert des gemischten Produktes ist . |
| |
|
 |
Damit haben wir für <RN2> |
|
|
|
|
 |
Das ist eine etwas ungewöhnlich Definition einer Funktion <RN2> mit der diskreten Variablen N, nämlich eine rekursiv
definierte Funktion. Wie löst man so eine Gleichung? Per Induktion: Schluß
von n auf n + 1. |
|
 |
Wir erhalten für die gesuchte Formel des eindimensionalen
"random walks": |
|
|
|
 |
Wer's nicht glaubt, beweist das ganze mit vollständiger Induktion. |
|
 |
Mit N = 1 anfangen; das Ergebnis für N = 2 verwenden,
dann Schluß von N auf N +1 |
 |
Random walk in drei Dimensionen
ergibt nichts grundsätzlich neues. Da die drei Richtungen unabhängig voneinander sind, wird unser besoffener Vogel (der Volltrunkene von oben schafft nur zwei
Dimensionen) auf jeder Achse i = x, y, z
sich um |
| |
| <R2i, N (3-dim)> |
= | N · a2 |
|
|
| |
entfernt haben. |
 |
Das
mittlere Abstandsquadrat - so heißt es ab jetzt immer - im dreidimensionalen ist damit . |
| |
| <R2N (3-dim)> |
= |
<R2x, N> + <R2y,
N> + <R2z, N> |
= | 3 · N · a2 |
|
|
|
 |
Oft ist man aber bei der Behandlung derartiger Probleme "großzügig"
und läßt den Faktor 3 unter den Tisch fallen - man bewegt sich sowieso fast immer im Bereich mehr oder
weniger heftiger Näherungen. |
 |
Dieses simple Gesetz ist eine der wichtigsten Formeln
bei Diffusionsvorgängen; wir werden es noch oft brauchen! |
|
 |
Die Formel besagt, daß das mittlere Abstandsquadrat bei einem beliebigen Random Walk
(wir haben keine Einschränkungen für R und a
gemacht) proportional zur Zahl der Sprünge (und damit zur Zeit) und zum Quadrat der (mittleren) Sprungweite ist. |
|
 |
Selbst im superallgemeinsten Fall, in dem R und a
nicht mehr konstant sein müssen, gilt die Formel noch, falls wir die Mittelwerte dieser Größen nehmen |
 |
Die Verknüpfung zur echten Diffusion von Teilchen ist nun einfach, denn: |
|
 |
Wir kennen die Zahl
N der Sprünge, d.h. die Sprungrate r mal Zeit t, auch
aus der Betrachtung der Leerstellenhüpferei: Eindimensional und in kubischen
Kristallen galt |
| |
| | D = |
r · a02
6 |
| | |
| | |
| Þ | r
= | 6 · D
a02 | |
|
|
|
 |
Dabei war a0die Gitterkonstante und D der Diffusionskoeffizient. |
|
 |
Damit erhalten wir |
|
|
| N = |
r · t | = |
6 · D · t
a2 |
| | |
| |
| <RN2>
= | N · a2 | = |
6 · D · t · a2
a02 |
|
|
 |
Ziehen wir die Wurzel aus <RN2> (und das ist nicht dasselbe wie die Wurzel aus RN2!),
erhalten wir den die mittlere Entfernung vom Startpunkt, die wir die Diffusionslänge
L nennen wollen. Es gilt: |
|
|
| L = |
æ
è |
<RN2
> | ö
ø |
1/2 | = |
a
a0 |
· | æ
è
| 6 · D · t |
ö
ø | 1/2 |
|
|
|
 |
Für beliebige Kristalle erhalten wir mit dem Geometriefaktor g statt dem 1/6 |
| |
| L = | = |
a
a0 · g |
· | æ
è
| D · t |
ö
ø | 1/2 |
|
|
|
 |
Falls wir Atome mit einer Sprungweite von |a| »
a0, Kristalle mit g = 1, und das ganze noch dreidimensional betrachten, erhalten wir schließlich die sehr wichtige Endformel |
| |
|
|
 |
Das "»" berücksichtigt, daß die
exakte Berücksichtigung der (gitterabhängigen) Sprungweite und der Dreidimensionalität den Vorfaktor i.a.
dicht an 1 rückt. |
 |
Wir haben, allgemein gesprochen, eine Fornel erhalten, die uns das Ergebnis eines
statistischen Prozesses an die Zeitdauer koppelt, für die der Prozess läuft. |
|
 |
Das gilt für jeden solchen Vorgang, also auch für
alle Diffusionsphämomene. Ob Leerstellen in einem Kristall wandern, Tintenmoleküle in Wasser, Elektronen in Halbleiter,
oder was auch immer; solange sie es mit "Random Walk" tun, gelten die obigen Beziehungen. |
 |
Am Rande sei noch bemerkt, dass wir das Ergebnis natürlich auch über
die Fickschen Gleichungen (plus atomare Deutung des Diffusionskoeffizienten) erhalten können: |
|
 |
Wir lösen ein passendes Diffusionsproblem (es wird uns eine Gaussverteilung geben) und
errechnen aus der Lösung den mittleren Abstand wie im Link angedeutet.
Das ist aber nicht so allgemein wie die Betrachtung hier - und mathmatisch ziemlich anspruchsvoll. |
© H. Föll (MaWi 1 Skript)