|
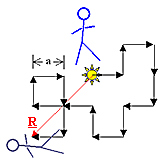
"Random Walk" = Schrittweise Bewegung mit gleicher Wahrscheinlichkeit
für jede Schrittmöglichkeit. | |
|
|
 |
Zentralfrage: Wie groß ist mittlerer Abstand
<R2 = R zwischen Startpunkt und Endpunkt nach N
Schritten mit Schrittweite a | |
|
 |
Schwere Frage, einfache Antwort:
(i = 1,2,3 für ein-, zwei- oder dreidimensionalen
RW). | |
|
| |
|
|
|
| <R2i, N (i-dim)> = R2
= i · N · a2 |
|
| |
|
| |
| |
 |
Mit N = r · t, der Sprungrate r
aus den alten Beziehungen sowie der Verknüpfung von r mit dem Diffusionskoeffizienten D,
erhält man für die Diffusionlänge
L, dem mittleren Abstand vom Startpunkt als Funktion der Zeit, eine fundamentale
Beziehung, die wir noch oft brauchen werden: | |
| L(t) = |
æ
è |
<RN2(t) > |
ö
ø | 1/2 |
= | a
a0 | · |
æ
è |
6 · D · t |
ö
ø | 1/2 |
| | |
| | |
| | |
| | |
|
| L(t) |
| |
| |
» |
| |
æ
è |
D · t |
ö
ø |
1/2 |
|
|
|
 |
Schrittweite a und Gitterkonstante a0 sind nicht immer
identisch, aber i.d.R. nicht sehr verschieden. | |
|
 |
Die Näherungsformel ist praktisch immer gut genug. |
|
© H. Föll (MaWi 1 Skript)