|
Kinetik bedeutet hier: Lehre vom Weg ins Gleichgewicht durch Bewegung
(von Atomen) mit "Nettoeffekt" und "Bewegung" im TD GG ohne
"Nettoeffekt" | |
|
|
 |
Weg Nichtgleichgewicht Þ Gleichgewicht: Es muss
sich netto "was" ändern! | |
|
 |
Bei Festkörpern / Kristallen: Atome müssen diffundieren |
|
 |
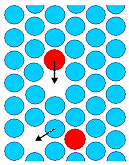
Zu betrachtender Elementarprozess: "Sprung"
eines Teilchens (=Atom). | |
|
 |
Atome "springen" aber auch im Gleichgewicht! Was zählt ist nur der Nettoeffekt
(im Gleichgewicht=0) | |
|
 |
Analogie: Girokonto. Kein Nettoeffekt falls Zufluß=Abfluß |
|
|
| |
|
 |
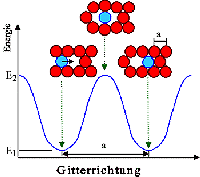
Sprünge erfolgen immer über Energiebarrieren
(besser: Enthalpiebarrieren). | |
| r = n · p(DE) |
n=Anlauffrequenz;
p(DE) Wahrscheinlichkeit zur
Überwindung der Energiebarriere DE |
|
|
 |
Ansatz für Sprungrate r=Zahl Sprünge eines
Teilchens pro Sekunde: | |
| |
| |
 |
Für p(DE) gilt immer
der Boltzmannfaktor: | |
|
|
 |
Extrem wichtige Gleichung; wird sehr häufiig auftauchen! |
|
|
 |
p(DE) für Atome in einem Kristall ist
die Wahrscheinlichkeit dafür, dass in den Vibrationen um die Ruhelage (mit "statistischen" Amplituden) die
Energie DE steckt. | |
| |
| |
 |
Damit Gesamtsprungrate R von N Teilchen über
Barriere E. | |
| R | = N · r = A · exp – |
E
kT |
|
|
|
 |
Vorfaktor A enthält die Anlauffrequenz n
und evtl. noch andere ("unwichtige") Faktoren | |
| | | |
| |
 |
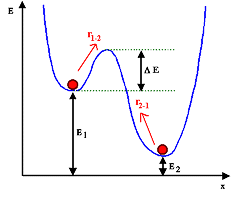
Gleichgewicht zwischen zwei E-Niveaus 1
und 2 bedingt
R1-2=R2-1 |
|
|
|
 |
Damit Zentralformel für die "Besetzung"
von E-Niveaus im TD GG | |
|
 |
Entscheidend ist nur E1 – E2; DE
bestimmt nur, wie lange es dauert, bis GG eingestellt ist. |
|
|
| |
| |
 |
Verallgemeinert und mit leichter Näherung (Ni <<
N0) erhält man eine Zentralformel der Materialwissenschaft: |
|
|
|
 |
Verteilung klassischer Teilchen im TD GG auf gegebene
Energieniveaus Ei mit Grundniveau E0=0 eV für alleSysteme. |
|
|
 |
Diese Art der Verteilung von Teilchen auf verschiedene E-Niveaus heißt Boltzmannverteilung
oder Boltzmannstatistik. |
|
|
 |
Bedeutung Boltzmannstatistik: Nie mehr Abzählen und Kombinatorik
für Entropieteil der freien Energie / Enthalpie!. |
|
|
| |
| |
 |
Anwendung auf atomare Fehlstellen (AF) im TD GG: |
|
|
|
 |
Teilchen (i.d.R.=Atome) habe zwei E-Niveaus: Grundniveau E0
auf Gitterplatz, und "angeregtes" Niveau EF (=Bildungsenergie) bei Bildung einer AF |
|
| |
| |
| |
 |
Fremdatome (FA) springen entweder als Zwischengitteratome ("i")
direkt, oder als substitutionelle FA indirekt über Leerstellen ("V"). Was für substitutionelle
oder interstitielle FA gilt, muss aber automatisch auch für die "normalen" Gitteratome gelten; man
spricht dann von "Selbstdiffusion". | |
| ri(ein i) = n · exp |
SM, i
k |
· exp – |
EM,i
kT | = |
Di · exp – |
EM,i
kT |
|
| rV(alle V) |
= DV · exp – |
EM, V
kT |
· exp – |
EF,V
kT |
|
Typische Wanderungsenergien
» 0,5 eV für die Zwischengitteratome
» 1 eV für Leerstellen. |
|
|
 |
Die zu überwindende Energiebarriere heißt EM=
Wanderungsenergie (oder Migrationsenergie) des betrachteten Teilchens; die jeweiligen
Sprungraten r sind damit gegeben. | |
|
 |
Der Vorfaktor D enthält im wesentlichen die Anlauffrequenz n
und die "Wanderungsentropie"
SM. Der Term exp-(SM/k) ist aber » 1 |
|
|
 |
In rV für alle Atome steckt
auch die Konzentration der Leerstellen, da die Wahrscheinlicheit des Sprungs eines Gitteratoms das Produkt der Sprungwahrscheinlichkeit und der Wahrscheinlichkeit, eine Leerstelle
als Nachbar zu haben, ist. (Es springen immer genau so viele Atome wie Leerstellen). |
|
| | |
| |
 |
Wichtig ist die Diffusionsstrom(dichte)
jDiff=Zahl der Teilchen, die pro Sekunde durch die Einheitsfläche A springen. |
|
|
|
 |
[jDiff]=s–1 · cm–2 |
|
|
 |
Wichtig ist die Unterscheidung zwischen Partialstrom (nur
links Þ rechts oder rechts Þ links) und Nettostrom=Differenz
der Partialströme. | |
|
 |
Nettoströme können =0 sein trotz großer Partialströme! |
|
|
| |
| |
 |
Die beiden empirisch gefundenen Fickschen Diffusiongesetze beschreiben:
| |
¶c
¶t | = D · |
æ
ç
è |
¶2c
¶x2 | + |
¶2c
¶y2 | + |
¶2c
¶z2 |
ö
÷
ø |
= D · Dc |
|
|
|
 |
1. Den Nettodiffusionstrom als Konsequenz eines
Konzentrationsgradientens Ñc(r) |
|
|
 |
2. Die zeitliche Änderung der Konzentration in einem Volumenelement bei r
aus der Bilanz des Zu- und Abflusses; sie ist proportional zur 2. Ableitung der Konzentration. |
|
|
 |
In beiden Gleichungen taucht dieselbe Proportionalitätskonstante auf, sie heißt
Diffusionskoeffizient. | |
|
 |
Die vermeintlich simplen Differentialgleichungen haben i.d.R. komplizierte Lösungen,
die typischerweise statistische Funktionen enthalten. | |
 |
"Random Walk"=Schrittweise Bewegung mit gleicher Wahrscheinlichkeit
für jede Schrittmöglichkeit. | |
|
|
 |
Zentralfrage: Wie groß ist mittlerer Abstand
<R2=R zwischen Startpunkt und Endpunkt nach N
Schritten mit Schrittweite a | |
|
 |
Schwere Frage, einfache Antwort:
(i=1,2,3 für ein-, zwei- oder dreidimensionalen
RW). | |
|
| |
|
|
|
| <R2i, N (i-dim)> = R2
= i · N · a2 |
|
| |
|
| |
| |
 |
Mit N=r · t, der Sprungrate r aus
den alten Beziehungen sowie der Verknüpfung von r mit dem Diffusionskoeffizienten D, erhält
man für die Diffusionlänge
L, dem mittleren Abstand vom Startpunkt als Funktion der Zeit, eine fundamentale
Beziehung, die wir noch oft brauchen werden: | |
| L(t) = |
æ
è |
<RN2(t) > |
ö
ø | 1/2 |
= | a
a0 | · |
æ
è |
6 · D · t |
ö
ø | 1/2 |
| | |
| | |
| | |
| | |
|
| L(t) |
| |
| |
» |
| |
æ
è |
D · t |
ö
ø |
1/2 |
|
|
|
 |
Schrittweite a und Gitterkonstante a0 sind nicht immer
identisch, aber i.d.R. nicht sehr verschieden. | |
|
 |
Die Näherungsformel ist praktisch immer gut genug. |
|
© H. Föll (MaWi 1 Skript)