|
| |
Eindimensional |
Zweidimensional |
Dreidimensional |
| (1) |
Wahrscheinlichkeitsdichte Teilchen nach N Sprüngen bei
(x,y,z) zu finden
mit Sprungweite "1". |
w(x,y,z) = |
æ
è |
1
2pN |
ö
ø |
1/2 |
· exp – |
x2
2N |
|
æ
è |
1
2pN |
ö
ø |
· exp – |
x2 + y2
2N |
|
æ
è |
1
2pN |
ö
ø |
3/2 |
· exp – |
x2 + y2 + z2
2N |
|
| (2) |
Breite auf 0,607 facher
(= e–1/2)
Höhe = 2s |
|
sx = Nx1/2 |
sx = Nx1/2
sy =Ny1/2 |
sx = Nx1/2
sy = Ny1/2
sz = Nz1/2 |
| (2a) |
Damit:
"Normaldarstellung
" von (1) |
w(x,y,z) = |
æ
è |
1
2s2p |
ö
ø |
1/2 |
· exp – |
x2
2s2 |
|
æ
è |
1
2s2p |
ö
ø |
· exp – |
x2 + y2
2s2 |
|
æ
è |
1
2s2p |
ö
ø |
3/2 |
· exp – |
x2 + y2 + z2
2s2 |
|
| (3) |
Volumenelement
DV bei Übergang zu Abständen r
| DV = |
2Dr
(der Faktor 2 ist wichtig!) |
2prDr |
4pr2Dr |
| (4) |
Absolute Wahrscheinlichkeit
W(r), Teilchen im Abstandsintervall
r, r + Dr zu finden mit dimensionloser Sprungweite "1"
W'(r) ist die Wahrscheinlichkeitdichte bezogen auf Abstände |
W(r) = w(r)DV =W'(r)Dr
|
æ
è |
2
pN |
ö
ø |
1/2 |
· exp – |
r2
2N |
· Dr |
|
æ
è |
r
N |
ö
ø |
· exp – |
r2
2N |
· Dr |
|
2r2
N |
· |
æ
è |
|
1
2pN |
ö
ø |
1/2 |
· exp – |
r2
2N |
· Dr |
|
| (5) |
Absolute Wahrscheinlichkeit Teilchen im Abstandsintervall
r, r + Dr zu finden mit Sprungweite a0 cm |
W(r,a0) =
w(r,a0)DV =
W'(r)Dr
|
æ
è |
2
a02pN |
ö
ø |
1/2 |
· exp – |
r2
2Na02 |
· Dr |
|
æ
è |
r
Na02 |
ö
ø |
· exp – |
r2
2Na02 |
· Dr |
|
2r2
a03·N |
· |
æ
è |
1
2pN |
ö
ø |
1/2 |
· exp – |
r2
2Na02 |
· Dr |
|
| (6) |
Mittleres Verschiebungsquadrat <r2>
= 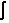 r2W'(r,a0)dr (mit Sprungweite a0 cm) = Diffusionlänge
L r2W'(r,a0)dr (mit Sprungweite a0 cm) = Diffusionlänge
L | <r2> = |
N·a02 | 2N·a02 |
3N·a02 |
| (6a) |
Diffusionlänge
L = {<r2>}1/2 |
L = | a0N1/2 |
a0(2N)1/2 | a0(3N)1/2 |
| (7) |
Mittleres Verschiebungsquadrat
mit dimensionloser Sprungweite "1" |
<r2> = |
N | 2N | 3N |
| (8) |
Wahrscheinlichstes rwahr aus
dW'/dr(rwahr) = 0 (mit Sprungweite "a0") |
rwahr = | 0 |
a0·N1/2 | a0(2N)1/2
siehe auch den Link |
| |
 |
3. Volumenelement |
|
 |
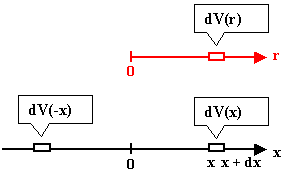
Wir beziehen uns nur auf Abstände. Die Volumenelemente
sind dann
- Eindimensional: Das Intervall r, + dr auf der Abstandsachse r
- Zweidimensional: Die Fläche zwischen den Kreisen mit Radius r und r + dr
-ein Ringsegment
- Dreidimensional: Das Volumen zwischen den Kugeln mit mit Radius r und r
+ dr - ein Kugelsegment oder eine "Zwiebelschale"
|
|
 |
Ein beliebter Fehler beim Übergang von cartesischen Koordinaten zu Polarkoordinaten für
den eindimensionalen Fall liegt im Übersehen des Faktors "2" in
der Beziehung
dV = 2 dr, den ein Wert für r = |x| deckt sowohl den Wert +x
als auch -x ab, wie die nachfolgende Zeichnung klar macht. |
|
|
|
|
 |
Es gibt keine negativen Abstände und damit keine negativen r. Teilchen die sich
im "Volumen"element bei x oder bei -x befinden, sind alle im Volumenelement bei r = |x|. |
 |
Der hier eventuell einfließende Fehler mag sich kompensieren (oder verstärken?),
wenn man einen anderen Faktor 2 Fehler macht, indem man Standardlösungen der Fickschen Diffusiongleichungen, die fast
immer für einen Halbraum gegeben werden (d.h. aus der Quelle diffundieren die Teilchen nur nach links oder
nur nach rechts; die Quelle sitzt auf der Oberfläche), mit den Random walk Ergebnissen vergleicht, bei denen die Teilchen
nach rechts und nach links diffundieren können (die Quelle sitzt im Inneren). |
| |
|
| |
 |
4. und 5. Absolute Wahrscheinlichkeit
und Wahrscheinlichkeitsdichten |
|
 |
Die absolute Wahrscheinlichkeit für irgendetwas muß
sich immer auf ein endliches (wenn auch differentiell kleines) Volumen beziehen. Denn die absolute Wahrscheinlichkeit, eine
endliche Anzahl von irgendwas bei einem von unendlich
viel mathematischen Punkten zu finden ist immer = 0. |
|
 |
Sind die Variablen in Wahrheit diskret (z.B. beim Würfelspiel, wo man schlicht keine
3,27 oder 7,005 würfeln kann), muß man immer die Wahrscheinlichkeitsdichte
über das Intervall um die diskrete Variable herum integrieren. Die Wahrscheinlichkeit eine 7 zu würfeln ist dann beispielsweise
|
| |
| w(7) = | 7,5
ó
õ
6,5 | w(r) · dV |
|
|
|
 |
Die angegebene Formel erhält man also einfach durch Multiplikation der Formeln in Reihe
1 mit den Formeln in Reihe 3. |
 |
Nach der Umrechnung auf Wahrscheinlichkeiten für Abstände
übernimmt W'(r) = W(r)/Dr die Rolle der Wahrscheinlichkeitsdichte - es ist jetzt
eine radiale Wahrscheinlichkeitsdichte. |
| |
 |
6. Mittleres Verschiebungsquadrat mit Sprungweite a0 |
|
 |
Diese Integrale können leicht berechnet werden indem man sie auf eine Form bringt, die
in Tabellen zu finden ist. Der jeweilige Wert des Integrals ist in der Formel durch rote Schrift
immer getrennt ausgewiesen. |
|
Eindimensional |
|
 |
Wir haben für das mittlere Verschiebungsquadrat
|
| |
| <r2>
= | æ
è
|
2
a02pN |
ö
ø |
1/2 |
· |
¥
ó
õ
0 |
r2 · exp – |
k · r2 | · dr |
= | æ
è |
2
a02 · p
· N | ö
ø |
1/2 | · |
p1/2
2k3/2 |
|
|
|
 |
Mit k = 1/ 2Na02 erhalten wir |
| |
| <r2> = |
æ
è |
2
a02 · p · N
| ö
ø |
1/2 | · |
N · a03 | · |
æ
è |
2p · N |
ö
ø | 1/2 |
= N · a02 |
|
|
 |
Zweidimensional |
|
 |
Wir haben für das mittlere Verschiebungsquadrat |
| |
| <r2> =
| æ
è |
1
N · a02 |
ö
ø |
· | ¥
ó
õ
0 |
r3 · exp – k · r2 · dr |
= | æ
è |
1
N · a02 |
ö
ø |
1
2k2 |
|
|
|
 |
Mit |
|
|
| k = |
1
2 · N · a02 |
; |
1
2k2 |
= | 4 · N2 · a04
2 |
= 2 · N2 · a04 |
|
|
|
 |
Damit ergibt sich |
|
|
| <r2> = |
1
N · a02 |
· |
2N2 · a04 |
= |
2N · a02 |
|
|
 |
Dreidimensional |
| |
| <r2> = |
2
a03 · N |
· |
æ
è |
1
2p · N |
ö
ø |
1/2 | · |
¥
ó
õ
0 |
r4 · exp – |
k · r2 | · dr |
|
|
|
 |
Mit |
|
|
| k = | 1
2N · a02 |
und | | |
¥
ó
õ
0 |
= |
3p1/2
8 · k5/2 | =
| 3p1/2· (2N · a02)5/2
8 |
|
|
|
 |
erhalten wir |
|
|
|
 |
Es ist immer gut, mal die Integration zu üben, aber
das ganze hätte man natürlich auch einfacher haben können: |
|
 |
Da die Hüpfe in x-, y- and z-Richtung unabhängig
voneinander sind, und deshalb Nx = Ny sein muß, gilt |
| |
| <r2(x,y)> |
= |
<r2(x)>2 + <r2(y)>2 | | | |
| | | = |
(Nxa02) + (Nya02) |
| | | | | = |
2Na02 |
|
|
|
 |
Für den dreidimensionalen Fall folgt entsprechend |
| |
|
 |
Unnötige Arbeit gemacht? Nein - nur dadurch läßt sich prüfen,
ob die Ausgangsformeln stimmen (so wurden die diversen Fehler in Büchern entdeckt). |
| |
 |
8. Wahrscheinlichstes r |
|
 |
Der wahrscheinlichste Abstand rwahr ist der Abstand, bei dem wir erwarten
können die meisten Teilchen zu finden. Daß das nicht derselbe Abstand ist
wie der mittlere Abstand
<r> = {<r2>}1/2 wurde schon anderweitig klargemacht. |
|
 |
rwahr ergibt sich offensichtlich aus dem Maximum der Verteilungskurve, d.h.
wir haben |
| |
|
|
 |
Wir bekommen: |
 |
Eindimensional: |
| |
æ
è |
2
a02 · p · N |
ö
ø |
1/2 |
· |
d
dr |
æ
è |
exp – |
r2
2Na02 |
ö
ø | = |
æ
è |
2
a02 · p
· N | ö
ø |
1/2 | · – |
æ
è |
r
Na02 |
ö
ø |
· exp – |
r2
2 · N · a02 |
= 0 |
|
|
|
 |
Und damit ganz schnell |
|
|
|
 |
Zweidimensional |
| |
d
dr |
æ
è |
r
N · a02 |
· exp – |
r2
2 · N · a02 |
ö
ø | = 0
|
|
. |
|
 |
Und damit |
|
|
|
 |
Dreidimensional |
| |
d
dr |
æ
ç
è |
2r2
a03 · N |
æ
è |
1
2p · N |
ö
ø |
1/2 | · exp – |
r2
2 · N · a02 |
ö
÷
ø |
= 0 |
|
|
|
 |
Und damit |
|
|
|
 |
Während rwahr und der Mittelwert von r, also die
Diffusionlänge L, bei eindimensionaler Diffusion fundamental verschieden sind, ist der Unterschied für
dreidimensionale Diffusion vernachlässigbar. Für Diffusion in hohen Dimensionen - was immer das sein mag - wird
der Unterschied offenbar immer kleiner. |
|
|
© H. Föll (MaWi 1 Skript)