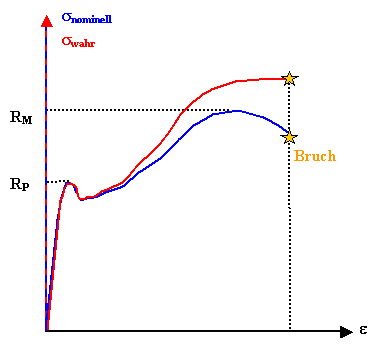
 |
Wieso hat die in Kapitel 7.1.1. gezeigte
Spannungs- Dehnungskurve ein Maximum (und die in Kapitel 8.2.1 gezeigten
nicht?). Die Antwort ist einfach: |
|
 |
Weil der Querschnitt der Probe immer kleiner wird, wir aber die Spannung s
in Kapitel 7 immer auf den Ausgangsquerschnitt bezogen haben. |
| |
Die "wahre" Spannung
s* (sie heißt wirklich so!) ist bei verringertem Querschnitt natürlich höher,
es gilt |
| |
| s* | = |
s
A* | | | |
| | A* = "wahrer" Querschnitt |
= | A
e + 1 |
|
|
|
|
(Folgt aus A* · l = A · l0 wg. Volumenkonstanz) |
|
Man kann also leicht von den nominellen Spannungen,
die immer auf den Ausgangsquerschnitt bezogen sind (engl."engineering strain") auf die wahre
Spannung beim Zugversuch umrechnen. |
|
|
Das ist natürlich nur bei großen Verformungen von Einfluß. Solange wir im elastischen
Bereich bleiben, lohnt es sich nicht. Bei plastischer Verformung ist es aber wichtig,
sich darüber im klaren zu sein, daß die Probe nur die wahren Spannungen spürt
und nicht die nominellen. |
|
Träg man die Spannungs - Dehnungskurve für die wahren
Spannungen auf, verschwindet das Maximum! Das haben wir für die Einkristallverformung
gemacht, denn für diese grundsätzliche Betrachtung ist die wahre Spannung, die Spannung am Ort der Versetzungen,
wichtig. |
| |
|
|
Mit den wahren Spannungen sind die Dinge zwar klarer - man kann ein Stück Kristall nicht
wirklich länger ziehen, indem man die am Ort der Versetzungen wirklich wirkende Spannung reduziert
- aber oft auch unpraktischer! |
|
|
Das Maximum der Verformungskurve, und damit die maximale Zugfestigkeit RM als
Materialparameter sind nicht mehr definiert oder zumindest nicht mehr leicht aus der Kurve zu entnehmen.
|
|
|
Das ist schlecht, denn RM hat eine weitere wichtige Bedeutung, die wir kurz streifen
werden |
| | |
|
Sobald das Maximum der nominellen Spannung in der Spannungs - Dehnungskurve erreicht ist, beginnt
die Probe sich einzuschnüren. |
|
|
Das sieht schematisch so aus: |
|
Und in der Realität so: |
| |
| |
|
|
Was hat das Maximum der Spannungs - Dehnungskurve und der Beginn der Einschnürung miteinander
zu tun? |
|
|
Die Antwort liegt in der Abhängigkeit der Spannungs - Dehnungskurve von der Dehnungsgeschwindigkeit
de/dt. Obwohl diese Abhängigkeit gering sein kann, wird man doch im allgemeinen
höhere Spannungen brauchen um dieselbe Dehnung bei höherer Dehnungsgeschwindigkeit zu erreichen; Beispiele sind im Link zu finden |
|
|
Betrachten wir eine Zugprobe, bei der ein kleiner Bereich 2 anfänglich eine größere
Dehnung hat als der restliche Bereich 2 - irgendeine kleine Inhomogenität, was auch immer. Die Frage ist: Wie
reagiert der Kristall? Wird Bereich 2 gebremst oder noch beschleunigt? |
|
|
Zur Antwort schauen wir auf das schematische Bild unten, das zwei Spannungs - Dehnungskurven
bei verschiedenen Dehnungsgeschwindigkeiten zeigt; wichtig ist dabei nur, daß die schnellere Dehnungsgeschwindigkeit
immer mehr Spannung braucht als die langsamere. |
| |
|
|
Da die Spannung immer überall gleich ist, liegt Bereich 2 links vom Maximum auf
der unteren Kurve, rechts vom Maximum auf der oberen Kurve mit der höheren Dehnungsgeschwindigkeit. |
|
|
Bereich 1 liegt links vom Maximum auf der oberen Kurve, dehnt sich also schneller und
wird Bereich 2 schnell einholen. Rechts vom Maximum wird Bereich 2 jedoch "davonlaufen" und sich
immer schneller dehnen. |
|
|
Dadurch wird die Probe im Bereich 2 dünner als im restlichen Bereich 1 -
Einschnürung erfolgt, und die nominelle Spannung kann zurückgehen, da die lokalen Spannungen im Bereich 2
trotzdem groß bleiben. Die Probe wird sich lokal immer schneller dehnen (wobei die gesamte mittlere Dehnungsgeschwindigkeit
trotzdem konstant bleibt) und schließlich brechen. |
|
Die maximale Zugfestigkeit (manchmal auch obere Streckgrenze
genannt) hat also eine signifikante und wichtige Bedeutung und es ist durchaus praktisch Spannungs - Dehnungsdiagramme mit
den nominellen und nicht mit den wahren Spannungen zu messen. |
|
|
|
Genauso wie die nominellen Spannung nur dann mit den wirklich im Material vorhanden Spannungen
annähernd identisch sind falls sich der Querschnitt nicht nennenswert ändert, die Verformungen also klein sind,
sind große Dehnungen
e ebenfalls fragwürdig: |
|
|
Denn Gesamtdehnungen können mit der nominellen Definition von e
genauso wenig durch Addition von einzelnen Dehnungen ermittelt werden, wie ein Gesamtzins aus der Addition von Einzelzinsen.
|
|
|
In anderen Worten: Ein mit 10 % (pro Jahr) verzinstes Guthaben von € 100 ist nach 5
Jahren eben nicht auf in Summe € 100 + 50% = € 150 angestiegen, sondern
auf
€ (100 + 10 + 11 + 12 + 13 + 14) = € 160.
Man nennt das Zinseszinsrechnung |
|
Mit der bisher benutzten nominellen Dehnung
e ist es offenkundig genauso. |
|
|
Für kleine Dehnungen (wie für kleine Zinssätze) ist
der Fehler den man durch Aufaddieren der Dehnungen macht nicht groß und man braucht sich keine Gedanken über
mögliche Konsequenzen zu machen. |
|
|
Für große Dehnungen jedoch, wie sie bei der plastischen
Verformung oder bei Elastomeren (dem Gummi) auftreten können, wird die Sache kritisch. Die insgesamt für eine
Verformung bis zu einem (großen) e1 aufzuwendende Arbeit P1
kann und darf nicht vom Weg abhängen, sie ist immer . |
|
|
|
|
|
Mit F = s* · A, l
= l0(e + 1), dl = l0 ·
de (A ist die (aktuelle) Querschnittsfläche) erhalten wir
|
| |
| P1 = A · l0 · |
e1
ó
õ
0 | s* · de |
|
|
|
|
Damit wird die spezifische Arbeit P1spez
pro Volumen V (= A · l0) |
|
|
| P1spez = |
P1
V | = |
e1
ó
õ
0 | s* · de |
|
|
|
Die insgesamt geleistete Arbeit kann und darf aber nicht davon abhängen, ob wir "in
einem Rutsch" bis e1 verformen, oder erst bis zu einem beliebigen Wert
e', und in einem zweiten Anlauf von e' bis e1. Wir müssen also fordern |
|
|
| P1spez = |
e1
ó
õ
0 | s de | = |
e'
ó
õ
0 |
s de + |
e1
ó
õ
e' | s de |
|
|
|
|
Diese Forderung ist bei nominellen Dehnungen nicht erfüllt - man
vergleiche die Aufteilung in Einzelsummen (= Integrale) bei der obigen Zinseszinsrechnung. |
|
Wir brauchen also eine Neudefinition der Dehnung, die auch
für große Dehnungen additiv ist. |
|
|
Dazu starten wir einfach mit einer inkrementell kleine Dehnung de; die
gesamte Dehnung erhalten wir dann durch Aufintegration - wie beim Zinseszins, nur daß wir kleine Inkremente (nicht
nur "Jahresscheiben") betrachten |
|
| Aus |
| |
|
|
|
wird dann |
| |
|
|
|
und es ist wichtig, daß wir jetzt dl
auf die real vorliegende Länge und nicht mehr auf l 0 beziehen. |
|
Damit wird die wahre Dehnung
e* - man nennt es wirklich so: |
|
|
| e* = | l
ó
õ
l 0 |
de = | l
ó
õ
l 0 | dl
l | = ln | l
l
0 |
|
|
|
Das ist im Prinzip eine bessere Definition der Dehnung als die nominellen Dehnungen - aber
wer mag schon mit Logarithmen rechnen wenn es nicht unbedingt sein muß?. |
|
|
Was man fast automatisch tut, ist den ln - Ausdruck in eine Reihe zu entwicklen. Und dann erhalten
wir für kleine
Dl die nominellen Dehnungen, wie es auch sein sollte: |
| |
| e* = | ln |
l
l 0 | = |
ln | l 0 + Dl
l 0 | = | ln |
æ
ç
è | 1 + |
Dl
l 0 |
ö
÷
ø |
» |
Dl
l 0 |
» e |
|
|
© H. Föll (MaWi 1 Skript)
8.2.1 Beobachtungen und Interpretation 
Mit Frame