9.2.2 Der E - Modul und sein "Ersatzschaltbild"

	Das elastische Verhalten eines Polymers - inklusive der Anelastizität und Viskoelastizität - läßt sich modellmäßig sehr einfach durch eine Art mechanisches "Ersatzschaltbild" beschreiben.
		Alles was wir brauchen ist eine ideale Feder:       und einen "Stoßdämpfer":
	Wir beschreiben diese Elemente durch ihre Bewegungsgleichungen.
		Die Feder enthält den E -Modul des Materials und beschreibt den perfekten elastischen Teil der Verformung durch
		e(t)  =  1 E · s(t)
		Ein Stoßdämpfer ist ein Element, das bei konstanter anliegender Spannung eine konstante Dehnungsgeschwindigkeit zeigt. Es gehorcht der Gleichung
		de(t) dt  =  1 h · s(t)
		Mit h = Viskosität des Materials; [h] = Pa · s = N · m–2 · s
	Das visko-elastische Verhalten der E(T) Kurve kann dann mit folgenden Ersatzschaltbildern beschrieben werden:

	Wie sich so eine Kombination Feder - Stoßdämpfer bei Belastung verhält, haben wir alle im Gefühl. Es ergeben sich tatsächlich die elastischen, und insbesondere anelastischen und viskoelastischen e(t) Kurven, die wir im vorhergehenden Unterkapitel beschrieben haben.
		Aber wir müssen es nicht im Gefühl haben - wir können es jetzt auch rechnen. Betrachten wir zum Beispiel das folgende Ersatzschaltbild.
				Wir können die Gesamtdehnung e als Summe der Einzeldehnungen e1 und e2 darstellen (wobei wir bei großen Dehnungen etwas aufpassen müssen).
				Freischneiden an den rot punktierten Stellen sagt uns, daß wir an Feder 2 die Spannung sF vorliegen haben; am Stoßdämpfer die Spannung sD. Beide zusammen entsprechen der externen Spannung sex die auch an Feder 1 anliegt.
				Damit haben wir die Gleichungen
				e  =   e1+ e2 sex  =  sF + sD e1  =  sex E1  e2  =  sF E2  de2 dt  =   sD h
		aus denen wir eine einfache Differentialgleichung für e2 erhalten:
		sex  =   e2 · E2  +  h · de2 dt
	Die Lösung mit der Anfangsbedingung e2(t = 0) = 0 ist
	e2(t)  =  sex E2 æ ç è 1  –  exp – æ è E2 h · t ö ø ö ÷ ø
		Addieren wir noch e1 = sex/ E1, die instantan erfolgende Dehnung der "in Serie" geschalteten Feder, bekommen wir als Gesamtlösung:
		e(t)  =  sex E1  +  sex E2 æ ç è 1  –  exp – æ è E2 h · t ö ø ö ÷ ø
		Dazu machen wir eine Übung
		Übung 9.2 -1 Rechnen mit mechanischem Ersatzschaltbild

	Die durch diese Lösung beschrieben Funktion e(t) für eine plötzlich ein- bzw. ausgeschaltete Spannung s sieht so aus
		Wir haben die Anelastizität modelliert.
	Mit einem geeignetem Ersatzschaltbild können wir so ziemlich jede viskoelastische und anelastische Dehnung beschreiben, vorausgesetzt wir wählen die geeigneten Parameter Ei und hi für die erforderlichen Federn und Stoßdämpfer.
		Ei und hi sind natürlich stark von der Temperatur und der Konformation abhängig.
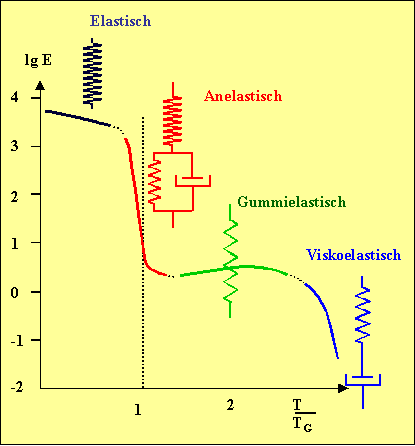
		Wir müssen uns jetzt fragen: Was bedingt die E und h der Elemente des Ersatzschaltbilds? Was sind die mikroskopischem Mechanismen der Anelastitzität, der Viskoelastizität, der Gummielastizität und so fort?
		Damit werden wir uns im nächsten Unterkapitel beschäftigen.

© H. Föll (MaWi 1 Skript)