6.3.2 Polarisationsmechanismen

Grundmechanismen

	Im Grunde müssen wir nur vier grundsätzliche Polarisationsmechanismen anschauen:
		Grenzflächenpolarisation . Grenzflächen wie Korngrenzen, Phasengrenzen usw. sind oft geladen und enthalten unkompensierte Dipole – schon weil es zum Beispiel in Ionenkristallen gar nicht anders geht. Wer's nicht glaubt, betätigt diesen Link.
		Atompolarisation (manchmal auch elektronische Polarisation genannt). Ein elektrisches Feld zieht immer die "Elektronenwolke" eines Atoms in eine Richtung, und den Atomkern in die andere. Als Effekt liegen die Ladungsschwerpunkte nicht mehr aufeinander – ein elektrisches Dipolmoment wird induziert.
		Ionische Polarisation. In diesem Fall muss die Bindung einen ionischen Anteil haben, d. h. die Atome sind mehr oder weniger geladen. Was dann im Prinzip passiert, haben wir uns schon angeschaut: Die vorhanden Dipole werden größer oder kleiner, heben sich also nicht mehr perfekt gegenseitig auf. Es wird ein Netto-Dipolmoment induziert.
		Orientierungspolarisation . Sie funktioniert mit elektrischen Dipolen erstmal nur bei Flüssigkeiten, die aus "polaren" Molekülen bestehen, d. h. aus Molekülen mit einem festen Dipolmoment, wie z. B. H2O. In einer Flüssigkeit kann sich das Dipolmoment mit dem Molekül in alle mögliche Richtungen drehen. Bei Wasser ohne elektrisches Feld mit wild herumwirbelnden Wassermolekülen werden auch alle Richtungen mit gleicher Wahrscheinlichkeit vorkommen. Mit elektrischem Feld werden die Dipolmomente alle etwas in Feldrichtung gedreht; wiederum wird ein Netto-Dipolmoment induziert.
	Das war's im Großem und Ganzen. Der 4. Mechanismus, die Orientierungspolarisation, interessiert uns hier aus zwei Gründen, obwohl wir uns sonst eher nicht mit Flüssigkeiten abgeben:
		Er ist in (mathematisch) exakt identischer Weise der wichtigste Mechanismus wenn wir nicht elektrische, sondern magnetische Dipole anschauen, d.h. magnetische Materialien betrachten. Deshalb nehmen wir ihn hier mal mit. Er steckt hinter dem, was in der "Mikrowelle" so passiert. Und das sollte der ET&IT-Ing. seinem Gspusi oder der Verwandschaft schon erklären können.
	Jetzt schauen wir uns diese Mechanismen noch etwas im Detail an:

	Grenzflächenpolarisation
	Grenzflächenpolarisation ist wichtig, aber kann nicht einfach berechnet werden – sie hängt halt von vielen Dingen ab.
		Dielektrika mit großer Suszeptibilität bzw. Dielektrizitätskonstanten in "billigen" Kondensatoren nutzen die Grenzflächenpolaristion in zusammengesintertem Zeugs mit kleinen Körnern und daher vielen Grenzflächen.
		Sie sind "billig", weil ihr Frequenzverhalten, Durchbruchsverhalten und sonstige Qualitätsmerkmale nicht spitze sind. Und das liegt auch am Dielektrikum!
		In integrierten Schaltungen sind Ladungen an den vielen Grenzflächen – die Ursache für die Grenzflächenpolarisation – oft absolut tödlich. Ein Großteil der Forschung und Technik im Bereich Mikroelektronik oder Solarzellen dreht sich um dieses Phänomen, das dann allerdings üblicherweise unter anderen Bezeichnungen läuft.
	Mehr dazu brauchen wir erst mal nicht zu wissen.

	Atompolarisation
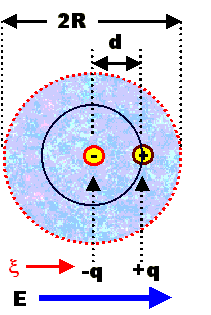
	Wenn wir ein stark vereinfachtes sphärisches Atom in ein elektrisches Feld stecken, bekommen wir sowas:
				Die Elektronenhülle hat's etwas nach links, den Atomkern etwas nach rechts gezogen, die Ladungsschwerpunkte liegen jetzt um ein x auseinander – damit ist ein Dipolmoment z · e · x induziert worden (z = Ordnungszahl, e = Elementarladung).
				Das äußere Feld E zieht die Ladungen auseinander, die innere Coulombwechselwirkung zieht sie zurück – ganz so, als ob die Ladungen durch eine Feder gekoppelt wären. Das Kräftegleichgewicht bestimmt, wie groß x sein wird. Ohne groß zu rechen, können wir für x << R (d. h. sehr viel kleiner als die Atomgröße) annehmen, dass x µ E sein wird.
				Damit können wir drei wichtige Schlussfolgerungen ziehen: Atompolarisation funktioniert immer . Ein Teil der Suszeptibilität bzw. Dielektrizitätskonstante jedes Materials kommt von diesem Polariationsmechanismus. Wir haben (was wir ja wollten) "bewiesen", dass für die Atompolarisation P µ E gilt. Wir haben außerdem den Frequenzgang schon im Prinzip bestimmt: Wenn wir ein elektrisches Wechselfeld mit der Kreisfrequenz w = 2pn anlegen, wackeln wir periodisch an einer kleinen Masse (die der Elektronenwolke), die über eine Feder an einem sehr schweren Gegenstand (dem Atomkern) hängt. Bei irgendeiner Frequenz sollte dann Resonanz auftreten – die Schwingungsamplitude wird groß!
	Wie wichtig ist die Atompolarisation in der Praxis? Anders gefragt, bei welchen Materialien ist die Suszeptibilität / Dielektrizitätskonstante überwiegend durch diesen Mechanismus bestimmt?
		Wir merken uns nur zwei Punkte dazu: Bei halbwegs sphärischer Verteilung der Elektronen um ein Atom ist der Mechanismus sehr schwach . Die Dielektrizitätskonstante der Edelgase ist z. B. nur unwesentlich größer als 1. Bei nicht-sphärischer Verteilung der Elektronen, wie z. B. in den kovalenten Bindungen aller relevanten Halbleiter, ist der Effekt sehr stark!
		Die Suszeptibilität / Dielektrizitätskonstante von Halbleitern wie Silizium kommt überwiegend von der Atompolarisation er(Si) = 12 er(Ge) = 16

	Ionische Polarisation
	Dieser Polarisationsmechanismus wirkt primär in Ionenkristallen wie NaCl oder LiF, aber auch in allen Kristallen mit ionischer Komponente wie SiO2 oder so gut wie allen anderen Oxiden (die Sauerstoffatome binden die Elektronen fast immer etwas fester als der Rest, sind also netto etwas negativ geladen).
		Wie zuvor gilt: Das Feld zieht die vorhandenen Dipole auseinander oder drückt sie zusammen – es wird ein Netto-Dipolmoment induziert. Das Feld zieht oder drückt dabei gegen die "Bindungspotentialfeder"!
		Aha – das haben wir gehabt! Die "Federkonstante " einer Bindung war Y · a, mit Y = Elastizitätsmodul, wie wir ihn hier nach englischem Vorbild ("Youngs Modulus") nennen wollen, um Verwechslungen mit dem Buchstaben "E" für das elektrische Feld auszuschließen; a ist der Bindungsabstand oder ungefähr die Gitterkonstante.
		Wir können damit sogar berechnen, mit welcher Kraft F an einem Ion mit Ladung q gezogen und bei welcher Auslenkung x Kräftegleichgewicht herrschen wird. Wir haben (immer nur mit Beträgen der Kräfte)
		Feldkraft auf Ladung:    Felek  =   q · E         Rückziehende Bindungsfederkraft:    F Bindg  =   Y · a · x         Kräftegleichgewicht zur Auslenkung x     Y · a · x  =   q · E         Þ   Auslenkung |x|    |x|      =   q · E Y · a
	Damit können wir jetzt hergehen und im Prinzip die DK oder die Suszeptibilität von Ionenkristallen berechnen.
		Tun wir aber nicht, sondern nehmen nur zur Kenntnis: Der Effekt kann groß sein; Ionenkristalle haben verhältnismäßig große Suszeptibilitäten, siehe die Tabelle.
	Was aber auch ohne Übung jetzt klar sein sollte: Im dielektrischen Verhalten der Materie steckt schon jetzt die "Mechanik" und "Thermodynamik" – Bindungspotentiale, Elastizitätsmodul, mittlere Geschwindigkeiten – wir haben das alles nicht nur aus Jux und Tollerei gelernt!

	Orientierungspolarisation
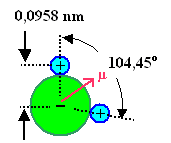
	Das Modell für diesen Polarisationsmechanismus ist Wasser – H2O. Schauen wir uns das "Wasserbild" noch mal genauer an:
		P = 0
	Was wir sehen, ist eine Momentaufnahme mit ganz kurzer Belichtungszeit. Die Wassermoleküle sind in ständiger Bewegung – sie laufen und rotieren; wir wissen im Prinzip sogar wie schnell! Ja? OK – Zeit für eine Übung.
		Rechenübung Aufgabe 6.3-1
		Das Dipolmoment eines Wassermoleküls ist übrigens 1,84 Debye. (1 Debye = 3,33564 · 10–30 Cm; warum soll immer nur ich blöde alte Zahlenangaben umrechnen? Mach's mal selber!)
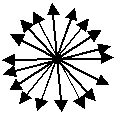
	Die wassereigenen Dipole führen also einen rasenden Tanz auf: Ihr Dipolmoment macht einen "random walk" bezüglich der Richtung und des Ortes. Die Vektorsumme aller Dipolmoment wird sich sehr exakt zu Null addieren.
		Schalten wir jetzt ein elektrisches Feld ein, wird der Dipol versuchen, sich in Feldrichtung auszurichten, denn daduch gewinnt er Energie. Anders ausgedrückt. Sein pos. Kopf will sich so nahe als möglich zum negativen Feldpol orientieren, denn er wird von ihm angezogen, sein negativer Hintern aus denselben Gründen zum Positivpol. Dazu muss der Dipol rotieren.
		Dazu hat er aber nicht viel Zeit. Sobald das Molekül wieder mit einem Kollegen kollidiert, haut's den Dipol wieder in eine Zufallsrichtung.
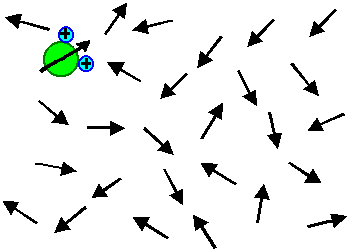
		Der Nettoeffekt bei realen Flüssigkeiten und realen Feldstärken (maximal um 10 MV/cm) ist einerseits sehr klein, d. h. die Vektorsumme ist nur leicht von Null verschieden, anderseits groß genug, um große Suszeptibilitäten zu machen – Wasser hat schließlich eine Dielektrizitätskonstante von um die 80! Es sieht schematisch etwa so aus:
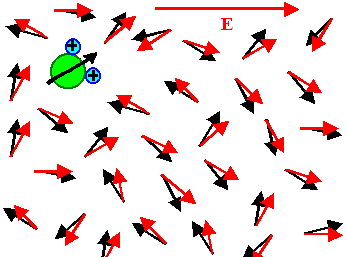		Ohne Feld Mit Feld
	Die Berechnung der Orientierungspolarisation ist zwar nicht besonders schwierig, aber mathematisch durchaus trickreich. Was wir tun müssen, ist klar: Wir minimieren wie immer einfach die freie Energie des Systems, um den Gleichgewichtszustand zu finden.
		Die Ausrichtung der Dipole im Feld "bringt" Energie, aber "kostet" Entropie, denn ein System mit ausgerichten Dipolen ist zweifelsohne ordentlicher als eines mit statistisch verteilten Dipolen. Wer wissen will, wie's geht, betätigt den Link.
		Was rauskommt, ist:
		P   =   NV · <m>   =   NV · m · L(b)           L(b)   =   coth (b )  –   1 b             b   =   m · E kBT
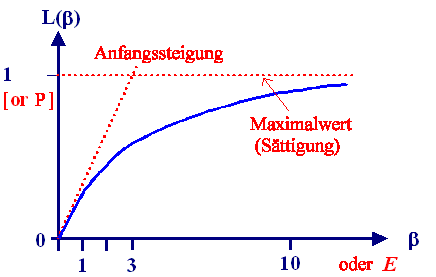
		L(b) heißt Langevin-Funktion , sie kommt in Problemen dieser Art häufig vor. Die Größen sind NV = Dichte der Dipole (d. h. der Wassermoleküle), <m> = Vektormittel der Dipolmomente, also P / NV. Das Ganze sieht so aus:
		Die Kurve zeigt quantitativ L(b); durch einfaches Umskalieren der Achsen erhält man aber exakt dieselbe Kurve für die Polarisation als Funktion der Feldstärke.
	Bei realistischen Feldstärken (unter ca. 10 MV/cm) und Temperaturen liegt man ganz in Anfangsbereich der Kurve – zwischen b = 0 und b < 1.
		Per Reihenentwicklung usw. bekommt man als gute Näherung für die mittlere Polarisation P:
		P  =   N · m 2 · E 3kBT
		Der Faktor N · m2 / (3kBT) wäre also die Suszeptibilität c = e r – 1 multipliziert mit der Vakuumpermittivität e 0 . Wir haben damit im Prinzip die Dielektrizitätskonstante von Wasser ausgerechnet und außerdem gezeigt, dass in guter Näherung die Polarisation proportional zur Feldstärke ist.
		Wir haben auch verstanden, warum eine bisher rein elektrische Größe wie die DK jetzt "plötzlich" temperaturabhängig wird!

	Zusammenfassung
	Wir haben zwei unserer drei Ziele erreicht:
		Wir haben im Prinzip gezeigt, dass die Polarisation immer proportional zur Feldstärke anwächst.
		Wir haben im Prinzip auch die Proportionalitätskonstanten, also die Suszeptibiltäten (und damit die DK) ausgerechnet! (Haha. Gottseidank gibt es den schönen Ausdruck "im Prinzip"!)
	Auf zur Verallgemeinerung des Begriffs "Dielektrikum"! Vorher aber noch ein paar schnelle Fragen:
		Fragebogen Schnelle Fragen zu 6.3.2

© H. Föll (MaWi für ET&IT - Script)