6.3 Polarisation und Polarisationsmechanismen

6.3.1 Ein paar wichtige Begriffe und Definitionen

Dipole und Polarisation

	Wir bleiben erstmal dabei, dass gute Isolatoren immer auch Dielektrika sind. Damit ist definiert:
		In Isolatoren gibt es keine beweglichen und damit frei verschiebbaren Ladungen (wie z. B die Elektronen in Metallen).
	Es gibt aber jede Menge mehr oder weniger ortsfeste Teilchen mit einer Ladung q: Ionen, Atomkerne, Elektronen in den Orbitalen um die Atome – die alle in einem elektrischen Feld die Kraft F=q · E erfahren.
		Alle diese geladenen Teilchen verursachen (zum Teil sehr große) elektrische Felder in Innern der Materie. Die Coulomb Anziehung hält schließlich die Ionen im Ionenkristall zusammen sowie die Elektronen um den Atomkern.
		Ein von außen angelegtes "externes" elektrisches Feld Eex wird aber auch irgendwie "gespürt" werden und zusätzliche Kräfte verursachen, die versuchen werden, die ansonsten ja gebundenen Teilchen etwas aus ihren Gleichgewichtspositionen zu verschieben. Mehr geht ja nicht.
	Betrachten wir mal die Anordnung der geladenen Teilchen in einem x-beliebigen Dielektrikum – Kristall, Flüssigkeit, Gas –, dann gibt es genau zwei für uns hier wichtige Möglichkeiten:
		Das Material enthält keine elektrischen Dipole. Das Material enthält elektrische Dipole
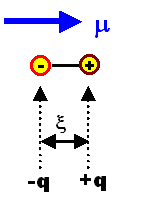
	Was ist ein elektrischer Dipol? Zwei entgegengesetzte Ladungen +q und –q beliebiger Größe (q kann dabei auch viel kleiner sein als eine Elementarladung) in einem Abstand x. Das hier:
		m  =  q · x
		Wir beschreiben einen solchen Dipol durch sein Dipolmoment m wie oben gegeben. Das Dipolmoment ist ein Vektor, der von der negativen zur positiven Ladung zeigt (entgegengesetzt wie das elektrische Feld!).
	Fein. Wie ist da jetzt mit den Dipolen und der Materie? Schau'n mer mal
		Dipole in Materie P=0
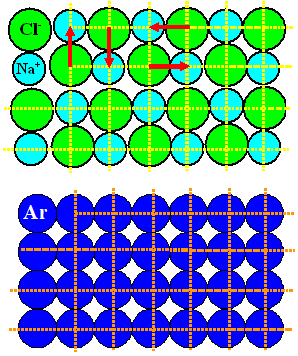
		Links oben ist ein schematischer NaCl Kristall gezeigt, der jede Menge Dipole enthält, egal wie man sie einzeichnet. Klar ist aber auch, dass die Vektorsumme Sm=0 der Dipolmomente gleich Null sein wird.
		Links unten ist ein Ar-Kristall gezeigt (gibt's bei tiefen Temperaturen). Vielleicht ein Exot, aber seine Basis wird aus exakt kugelförmigen neutralen Atomen gebildet, bei denen dann auch noch der Schwerpunkt der negativen Ladungen der Elektronen"wolken" exakt auf den Schwerpunkt der positiven Ladungen im Kern fällt. Da ist nirgends ein Dipolmoment! Daher gilt hier bereits m=0.
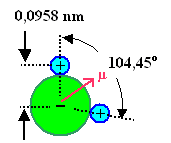
		Rechts oben sehen wir die Momentaufnahme von einem Stück (zweidim.) Wasser. Rechts unten wird klar, warum jedes Wassermolekül ein Dipolmoment mit sich herumschleppt, und warum die die Vektorsumme ohne Feld trotzdem im Mittel zu Sm =0 führt.
	Nun kommt der entscheidende Satz:
		Ein externes elektrisches Feld wird in einem Dielektrikum immer Dipole induzieren und zusätzlich die eventuell vorhandenen Dipole verändern.
	Der daraus zunächst resultierende Effekt heißt " Polarisation" P des Dielektrikums.
		Die Polarisation eines Materials mit dem Volumen V ist sehr einfach definiert:
		P  =  S m V  =  <m> · N V
		Dabei ist < m>= durchschnittliches oder Netto (Vektor) Dipolmoment= S m / Anzahl der Dipole und NV= Dichte der Dipole (per m3).
		Die Polarisation P ist also nichts anderes als der Gesamt- oder Nettoeffekt aller vektoriell aufsummierten Dipole pro cm3 .
		In allen obigen Fällen ist die Polarisation eines beliebigen Volumens ohne ein außeres Feld exakt P=0, weil sich entweder die Dipolmomente jedes Pärchens exakt aufheben oder sowieso keine da waren.
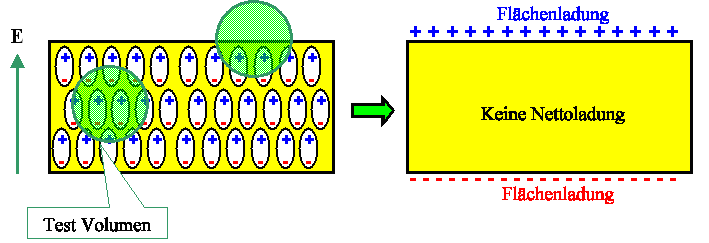
	Betrachtet man nicht Dipole, sondern einfach nur im Raum verteilte Ladungen pro Volumeinheit, also die Ladungsdichte r (x, y, z) (Aufpassen: wieder ein-und -dasselbe Symbol (r) für ganz verschiedene Sachen (spez. Widerstand oder Ladungsdichte), stellen wir fest, dass im Volumen r( x , y, z)=0 gilt – nur an der Oberfläche haben wir jetzt bei von Null verschiedener Polarisation eine Flächenladung .
		Diese Flächenladung ist nichts anderes als die Polarisation P – nicht umsonst hat sie die Dimension Ladung pro Fläche, C/cm 2. Mehr dazu im Link .
		Die Zeichnung veranschaulicht das:
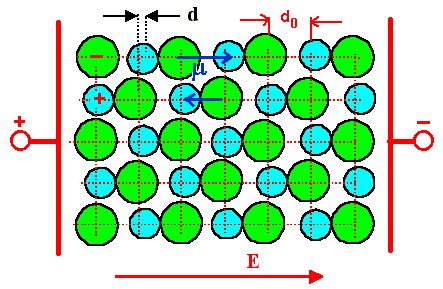
	Die Polarisation eines Materials ändert sich und wird von Null verschieden, sobald wir jetzt ein äußeres Feld einschalten. Unser Ionenkristall sieht dann beispielsweise so aus:
		Im Feld wie eingezeichnet zieht's die negativ geladenen Cl–-Ionen etwas nach links, die positiv geladenen Na+-Ionen etwas nach rechts. Die beiden Dipolmomente, die ohne Feld entgegengesetzt gleich groß waren, sind jetzt verschieden, da die Abstände x0 sich um ein ± Dx geändert haben.
		Auch im Ar-Kristall oder in jedem anderen Material wird sich bezüglich der Dipole im Feld was tun.
	Damit kommen wir zur Kernaussage:
		Ein externes elektrisches Feld polarisiert ein Dielektrikum

	Polarisation, Verschiebungsdichte, Suzeptibilität und Dielektrizitätskonstante
	Der klassisch geprägte ET&IT-Ingenieur reagiert jetzt mit "hä?", denn in einem Material, so hat man das doch gelernt, ersetzt man das elektrische Feld E durch die Verschiebungsdichte D=e0er E, und e0 ist die elektrische Feldkonstante oder Permittivität des Vakuums.
		Möglicherweise hat er oder sie auch gelernt, dass der moderne Elektrotechniker nicht mehr "Dielektrizitätskonstante" sagt, sondern Permittivität.
	Sei's drum. Zum einen sind es nur verschiedene Wörter für dieselbe Sache, zum anderen bestehen sehr einfache Beziehungen, die wir ohne weitere Kommentare oder Herleitung angeben:
		Sinnvolles Materialgesetz P  =  e0 · c · E Sinnvolle neue Materialkonstante c  =  dielektrische Suszeptibiltät Alte Materialkonstante er   =  c + 1 Beziehung D Û P D = e0 · E  +  P
		Die Verwendung vom Polarisiation und Suszeptibilität statt Verschiebungsdichte und Dielektrizitätskonstante ist aus Materialsicht "besser", weil sie Ursache und Wirkung klarer aufzeigt: das elektrische Feld ist die Ursache für die Polarisation. Der Gesamteffekt im Material wird beschrieben durch das dort vorhandene elektrische Feld plus die von diesem Feld verursachte Polarisation.
		Das heißt aber nicht, dass Verschiebungsdichte und Dielektrizitätskonstante nutzlos sind – man kann je nach Aufgabenstellung damit einfacher rechnen. Wir werden im folgenden zwar oft die Polarisation bemühen, aber meistens von der Dielektrizitätskonstante oder der DK reden, um die Verwirrung zu minimieren.
		Für uns heißt das zusammengefasst – die diversen Polarisationsmechanismen, die alle oben schon angeklungen sind, genauer zu betrachten.
	Hier sind die schnellen Fragen:
		Fragebogen Schnelle Fragen zu 6.3.1

© H. Föll (MaWi für ET&IT - Script)