|
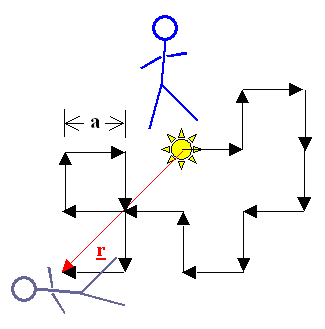
Ein paradigmatischer Volltrunkener kommt aus einer Kneipe und
torkelt durch die Gegend. Jeder Schritt führt mit gleicher Wahrscheinlichkeit nach vorne oder hinten, nach rechts oder
links. In welchem mittleren Abstand
<|r|>
von der Kneipe finden wir die hilflose Person nach N Schritten der (immer gleichen) Schrittlänge
a? |
| |
|
|
 |
Die Art der Fragestellung ist sehr wichtig. Wir können ähnliche, aber
in der Bedeutung doch ganz verschiedene Fragen stellen, zum Beispiel: |
|
|
| |
- In welchem mittleren Abstand
< |r|> = <(x2
+ y2)1/2> finden wir die hilflose Person? (Das ist die Frage
von oben.)
- Wo, d.h bei welchem mittleren Ort
< r>, finden wir im Mittel die hilflosen
Personen? (Offenbar bei r = 0!)
- Bei welchem Abstand |r| wahr ist es am wahrscheinlichsten,
den Trunkenbold zu finden? 1)
|
|
 |
Sei's drum! Wir interessieren uns hier nur für den mittleren
Abstand, den wir Diffusionslänge
L nennen. Offenbar hängt L von der Gesamtzahl N der Schritte ab (im Bild
sind es 16) und von der Schrittweite a. |
|
|
 |
In dem obigen Beispiel betrachten wir einen speziellen Fall des sogenannten Random Walk: Zwei
Dimensionen, feste Schrittweite, 4 feste Winkel.
| |
|
 |
Auf deutsch heißt Random Walk "statistische
Wanderung" oder Zufallsbewegung – aber nur der englische Ausdruck ist wirklich
geläufig. Man kann Random Walk für jeden Fall und ganz allgemein immer erzeugen,
indem man den nächsten Schritt in irgendeine der möglichen Richtungen mit einem geeigneten Würfel auswürfelt.
(1 = vor, 2 = zurück, 3 = ...) | |
| |
| |
|
 |
Wir können das mal experimentell machen. Eine Bewegung sei nur linear möglich
(Besoffene in der Mitte eines Tunnels). Statt eines Würfels nehmen wir eine Münze (Kopf = Schritt nach links,
Wappen = Schritt nach rechts. Wir lassen auch gleich einen Haufen Besoffene loslaufen (= Punkte), dann ergibt sich sofort
die Verteilung der individuellen Abstände und daraus der mittlere Abstand. |
|
 |
Wir können dieses einfache Experiment durchführen, indem wir eine Münze
werfen und unsere Teilchen bei "Zahl" nach rechts, bei "Kopf" nach links um eine Einheit (unsere Gitterkonstante)
bewegen. Das sieht dann beispielsweise so aus: |
|
|
Link
zum "Random
Walk"-Simulator
(leider defekt) |
|
 |
Spielt man ein bißchen mit dem Simulator oder wirft selbst eine Münze,
fällt schnell auf, daß ein Teilchen nach einigen Würfen in der Regel nicht mehr beim Ausgangspunkt ist,
obwohl die Wahrscheinlichkeiten für Schritte nach rechts oder nach links genau gleich groß sind. |
 |
Arbeitet man sich durch die Mathematik, erhält man für die Diffusionslänge
L = mittlerer Abstand nach N Schritten mit (mittlerer) Schrittweite a in ausreichender
Näherung: |
| |
| L2 | = | N · a 2 |
| | | L | = |
a · (N)½ |
|
|
|
 |
Betrachten wir jetzt nicht mehr Besoffene, sondern Atome oder Leerstellen mit vergleichbarer
Intelligenz, ist ihre Schrittweite rund und roh eine Gitterkonstante a, und die Zahl N der Schritte
oder Hüpfe ist ihre Sprungrate mal Zeit oder N =
r · t. |
|
 |
Die Sprungrate wiederum steckt im Diffusionskoeffizienten
des diffundierenden Teilchens. Setzt man alles zusammen, erhält man eine sehr wichtige und sehr simple Beziehung zwischen
der Diffusionslänge eines Teilchens (wie weit kommt es im Mittel?) und seiner Lebensdauer
t = verfügbare Zeit zum Rumrennen in der Form |
| |
|
 |
Diese Formel wollen wir uns gut merken! Wir haben, allgemein gesprochen, eine
Formel erhalten, die uns das Ergebnis eines statistischen Prozesses an die Zeitdauer koppelt, für die der Prozess läuft. |
|
 |
Das gilt für jeden solchen Vorgang, also auch für alle Diffusionsphämomene.
Ob Leerstellen in einem Kristall wandern, Tintenmoleküle in Wasser, Elektronen im Halbleiter
– was auch immer; solange es mit "Random Walk" geschieht, gelten die obigen Beziehungen. |
|
 |
Ausblick: In allen Formeln zu Halbleiterbauelementen steckt die Diffusionslänge
L = (Dt)½
der Ladungsträger, die mit der Lebensdauer t dieser Ladungsträger
und ihrem Diffusionskoeffizienten D durch unsere Random-Walk-Formel verknüpft ist. Zahlenwerte für
L und t (der Wert von D folgt dann aus der Formel)
sind deshalb sehr wichtige Kenngrößen für Halbleitermaterialien! |
 |
Am Rande sei noch bemerkt, dass wir das Ergebnis natürlich auch über
die Fickschen Gleichungen (plus atomare Deutung des Diffusionskoeffizienten) erhalten können. |
|
 |
Wir lösen ein passendes Diffusionsproblem (es wird uns eine Gaußverteilung geben)
und errechnen aus der Lösung den mittleren Abstand. Das ist aber mathematisch ziemlich anspruchsvoll. |
| |
|
© H. Föll (MaWi für ET&IT - Script)