|
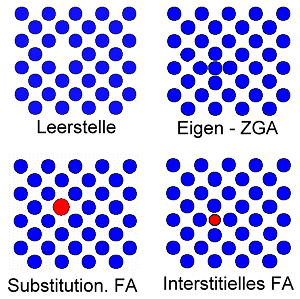
Es gibt vier Grundtypen atomarer Fehlstellen: |
|
|
|
 |
Die intrinsischen Fehlstellen Leerstelle (Index V
= "vacancy") und Eigen-Zwischengitteratom (ZGA; Index i = "interstitial") sind im thermodynamischen Gleichgewicht immer vorhanden, mit einer Dichte nV,i
oder der Konzentration (relative Häufigkeit) cV,i entsprechend |
|
|
| |
|
|
|
| nV,i | = |
N0 · exp ( – |
EV,iF
kB T |
) | | |
| | |
| cV,i = |
nV,i
N0 |
= | exp ( – |
EV,iF
kB T |
) |
|
| |
|
| |
| |
 |
Die Konzentration steigt also exponentiell mit der Temperatur. |
|
Leerstellen: EV,iF
» (0,5 - 2) eV
ZGA: E
V,iF » (2 - 5) eV
|
|
|
 |
Typische Bildungsenergien EV,iF liegen im Bereich um 1
eV. | |
|
 |
Merken:
kBT bei RT = ca. 1/40 eV = 25 meV. | |
 |
Die Konzentration der extrinsischen
AF ist i.d.R. durch die Qualität des Ausgangsmaterials bedingt; sie liegen dann in Über-
oder Untersättigung vor. |
|
|
| |
|
 |
Atomare Fehlstellen sind beweglich. Sie können im Kristall
diffundieren. | |
|
|
 |
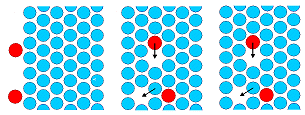
Intrinsische und extrinsische ZGA diffundieren direkt durch Sprünge auf äquivalente Nachbarpositionen. |
|
|
 |
Leerstellen diffundieren durch Sprünge der Nachbaratome in die Leerstelle. |
|
|
 |
Substitutionelle Fremdatome diffundieren über einen Leerstellenmechanismus
Þ | |
 |
Diffusion ist eine Grundtechnologie, insbesondere für Halbleitertechnik. |
|
|
| |
|
 |
Entscheidend ist die Sprungrate r: |
|
| r = |
n0 | ·
| exp ( – |
EM
kBT
| ) | | |
Zahl der
Anläufe / s | |
Wahrscheinlichkeit,
daß es klappt |
|
|
|
 |
n0 = Schwingungsfrequenz der Atome im Kristall
» 1013 Hz. |
|
 |
Wesentliche Erkenntnis: Der Boltzmannfaktor
exp[–E/(kBT)] ist die Wahrscheinlichkeit,
daß ein Teilchen innerhalb eines Ensembles bei der Temperatur T die Energie E "hat". |
|
|
| |
| |
 |
Makroskopische Diffusionsströme
j (= Teichen pro s und cm2) werden durch Dichtegradienten Ñn
getrieben: | |
| jx |
µ |
¶ n(x,y,z)
¶ x | | | | |
| j( r) | = |
– D · Ñn(r) |
| D(T) |
= |
a2 · r(T) |
= |
a2 · n
0 |
· exp ( – |
E M
kBT |
) |
| | |
| |
| |
| | |
= |
D0 · exp ( – |
EM
kB T |
) | |
|
|
|
|
 |
Das 1. Ficksche Gesetz koppelt Ströme und Gradienten. |
|
|
 |
Der Diffusionskoeffizient
D beschreibt Teilcheneigenschaften (a = Gitterkonstante). Typische Wanderungsenergien
EM (M: "migration") liegen im Bereich von 1 eV. |
|
|
 |
Das 2. Ficksche Gesetz beschreibt die zeitliche Änderung der Dichte.
| |
|
| |
|
|
|
¶n
¶
t | = D · | æ
ç
è
| ¶2n
¶x2 | + |
¶2n
¶
y2 | + | ¶2
n
¶ z2 |
ö
÷
ø |
= D · Dn |
|
| |
|
| |
|
|
 |
Diffusionsströme geladener Teilchen sind elektrische Ströme! | |
| | |
| |
|
 |
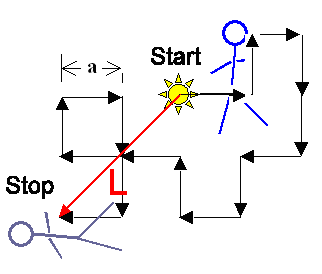
Diffundierende Teilchen machen einen "random walk": |
|
|
|
 |
Zwischen Schrittweite (meist » Gitterkonstante a),
Zahl der Schritte N, Diffusionskoeffizient D, "Laufzeit" t
und der Diffusionslänge
L gibt es einfache Zusammenhänge: | |
| |
| |
| |
| L2 | = | N · a2 |
| | | | | L | = |
(D · t )½ |
|
| |
|
| |
|
|
 |
Die letzte der beiden Gleichungen muß man wissen! |
|
| |
| |
| |
© H. Föll (MaWi für ET&IT - Script)