4.2.2 Diffusion mit atomaren Fehlstellen und Ficksche Gesetze

Atomare Diffusionmechanismen

Die Bedeutung der Diffusion in Kristallen (d.h. der Bewegung von Atomen in Kristallen) für die Technologie kann kaum überschätzt werden.

Betrachten wir als Beispiel die Standardaufgabe der Halbleitertechnik, die Herstellung eines MOS-Transistors. Folgende (stark vereinfachte) Struktur soll hergestellt werden:

Querschnitt durch einen einfachen MOS-Transistor

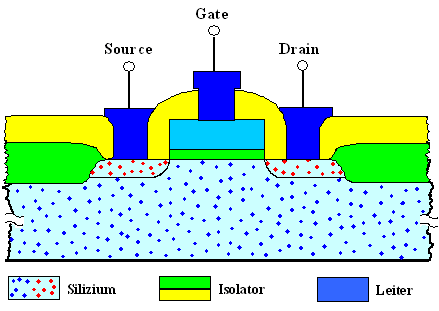
Entscheidend ist, daß der (hellblau gezeichnete) Si-Kristall ganz bestimmte substitutionelle Fremdatome enthält – die roten Punkte markieren z. B. Phosphor-Atome, die blauen Punkte Bor-Atome in Konzentrationen um 1 ppm.

Diese Fremdatome müssen bei der Herstellung des Transistors in die richtigen Bereiche des Kristall in der richtigen Konzentration eingebracht werden – aber wie?

Sie können dabei nur¹⁾von außen kommen, d.h. sie müssen durch die Oberfläche in den Kristall hinein diffundieren. Wie geht das? Der Kristall ist ja ein geschlossenes Gebilde; Atome können da nicht so einfach durchwandern. Wir haben eine Situation wie im nächsten Bild gezeigt.

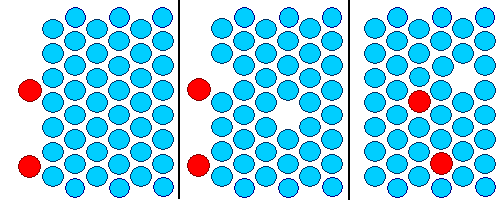Oben links ist die Ausgangssituation gezeigt.
Zwei rote Phosphoratome sitzen auf der Oberfläche und sollen ins Innere.
Das geht erst, wenn mal eine Leerstelle "vorbeikommt" (mittleres Bild).
Das rechte Bild zeigt dann die Situation etwas später.
Die beiden Atome sind etwas ins Innere gewandert, sitzen aber immer fest, bis mal wieder eine Leerstelle vorbeischaut!
Der Kristall ist dabei noch viel geschlossener, als es hier aus Gründen der Übersichtlichkeit gezeichnet ist.
Die Kugeln müßten sich ja berühren, oder sogar ein bißchen durchdringen, wenn richtige Bindungen vorliegen.

Gezeigt ist der Leerstellenmechanismus der Diffusion . Nur über diesen Mechanismus ist die Bewegung von Atomen auf Gitterplätzen möglich. In der Regel werden die Atome des Kristalls selber in eine benachbarte Leerstelle springen (man spricht dann von Selbstdiffusion), aber hin und wieder gelingt das auch der kleinen Minorität der substitutionellen Fremdatome. Das Ganze kann unten links mal animiert betrachtet werden:


Links: Leerstellenmechanismus der Selbstdiffusion; rechts: Diffusion interstitieller Fremdatome

Die Leerstelle selbst muß dabei notwendigerweise auch beweglich sein. Sie sitzt nicht immer am selben Platz, sondern bewegt sich durch das Kristallgitter in völlig statistischer Weise. Sie diffundiert, indem benachbarte Gitteratome mit ihr den Platz wechseln.

Damit wird klar, daß die Diffusiongeschwindigkeit, mit der sich ein Phosphoratom im Si-Gitter bewegen kann (oder jedes andere substitutionelle Fremdatom in jedem anderen Gitter) im wesentlichen davon abhängt, wie hoch die Leerstellenkonzentration ist und wie schnell sich die Leerstellen selbst bewegen.

Die entscheidende Größe für die Mobilität eines Fremdatoms ist seine Sprungrate (oder -frequenz) r, d.h. die (mittlere) Zahl von Platzwechseln pro Sekunde, mit der (im Mittel) sich eine Leerstelle auf einen Nachbarplatz bewegt oder, exakt dasselbe, ein Atom in die Leerstelle.

Die Diffusion von interstitiellen Fremdatomen kommt dagegen ohne Leerstellen aus. Hier hüpfen die Atome direkt von einem Zwischgitterplatz zum nächsten – wie oben rechts gezeigt. Interstitielle Fremdatome diffundieren deshalb häufig schneller als die substitutionellen.

Wie groß ist die Sprungrate von Leerstellen oder ZGAs – egal ob intrinsische oder extrinsische?

Wir wissen , daß die Atome mit einer Frequnz von ca. n₀ » 10¹³ Hz um ihre Gleichgewichtslage vibrieren. Anders ausgedrückt: Ein atomarer Nachbar einer Leerstelle nimmt ca. 10¹³ mal pro Sekunde einen Anlauf, um den großen Schritt in die Leerstelle zu machen. Wie oft ist das Atom erfolgreich?

Einfach: Zahl der Versuche pro Sekunde mal der Wahrscheinlichkeit, daß es klappt. Als Formel für die Sprungrate r ergibt sich

r =	n₀	·	exp (–	E^M k_BT	)
	Zahl der Anläufe / s		Wahrscheinlichkeit, daß es klappt

E^M ist dabei die Wanderungsenergie ("Migration"), d.h. die Energiebarriere, die das hüpfende Atom überwinden muss, um seinen Platz zu wechseln.

Für hüpfende Zwischengitteratome aller Arten gilt exakt dieselbe Gleichung, nur die Wanderungsenergien sind spezifisch.

Die Gleichung oben sollte Assoziationen auslösen! Sie enthält einen Boltzmannfaktor – exakt wie im vorhergehenden Modul definiert.

Ein Verdacht kommt auf: Ist ein Boltzmannfaktor schlicht eine Wahrscheinlichkeit? Falls ja, für was?

Die Antwort ist:

1. Ja

Falls ein "thermodynamisches System"			wie ein Kristall
verschiedene angeregte Energiezustände E_i oberhalb des Grundzustands hat
(wobei E₀ die Energie des Grundzustands [= Zustand mit der kleinsten Energie] ist),			Alle Plätze mit Atomen besetzt Þ E₀ := 0 eV
dann ist im thermodynamischen Gleichgewicht (d.h. bei einer bestimmten Temperatur)
die Zahl der "Teilchen" N_i			wie z.B. Leerstellen = Atome weg
bei der Energie E_i			hier: Bildungsenergie E^F
gegeben durch

N _i N₀	= exp	æ ç è	–	E_i k_BT	ö ÷ ø

Man kann diese Gleichung, die wir Boltzmann-Verteilung nennen und der wir hier zum ersten mal begegnen, gar nicht groß und dick genug schreiben!

Wir werden sie noch so oft brauchen, daß man gut daran tut, sie jetzt schon zu verinnerlichen.

In der Gleichung oben ist N₀ die Zahl der Teilchen bei der Energie E₀ = niedrigste Energie des Systems = Grundzustand; i.d.R. = 0 gesetzt.

Für insgesamt N_total Teilchen, wobei N₀ Teilchen, die auf dem Energieniveau bei E₀ = 0 eV "sitzen", und N₁ Teilchen bei E₁ > 0 eV, gilt N₀ = N_total – N₁ .

Falls aber nur sehr wenige Teilchen die höheren Niveaus besetzen, kann man N₀ » N_total annehmen; dann hat man in guter Nährung die einfache Boltzmann-Verteilung:

N_i	= N_total · exp	æ ç è	–	E_i k_B T	ö ÷ ø

Diffusionsstrom und 1. Ficksches Gesetz

Wir betrachten eine Horde Leute, die während einer Party in zwei gleichgroßen Sälen nur so umherwandern, ohne Ziel und Zweck. Das ist im Zweidimensionalen genau das, was eine Leerstelle im Kristall in drei Dimensionen macht.

Man nennt so eine Bewegung, bei der ein Schritt nach rechts genauso wahrscheinlich ist wie ein Schritt nach links oder nach vorne oder hinten (oder oben oder unten) eine Zufallsbewegung oder einen "random walk".

Die Wände betrachten wri als perfekt reflektierend. Nun öffen wie eine Tür ziwschen den Sälen. Hin und wieder wird nun eine Person rein zufällig durch die Tür hindurchtreten und dann im jeweils anderen Saal landen. Wie groß ist dann der Nettostrom von Personen, die pro Sekunde durch die Türfläche (= x m²) durchtreten?

Nach kurzem Nachdenken sollte klar sein:

Der Nettostrom, nennen wir ihn mal j, ist die Differenz der Teilströme: j = j_1®2 – j_2®1, d. h. er ist gleich der Zahl der Personen, die pro Sekunde vom Saal 1 in Saal 2 gelangten und umgekehrt.
Falls gleich viel Leute in beiden Sälen sind, d. h. falls die Dichten n₁ und n₂ der "Teilchen" gleich sind, gilt aus Symmetriegründen: j_1®2 = j_{2® 1}; der Nettostrom ist j = 0.
Falls n₁ > n₂, werden wir j µ n₁ – n₂ erwarten; es werden vom Bereich der höheren Dichte mehr Teilchen in den Bereich niedriger Dichte wandern als umgekehrt.
Es ist sinnvoll, nicht den Strom, sondern die Stromdichte (= Strom pro Fläche) zu betrachten.

Die Verallgemeinerung, die zum 1. Fickschen Gesetz führt, ist offensichtlich:

In einem Kristall mit der lokalen und momentanen Dichte n(x,y,z;t) = n(r;t) an statistisch herumhüpfenden Teilchen (= diffundierenden Teilchen) – wie Leerstellen, substitutionelle Fremdatomen (über Leerstellen) oder ZGA – fließt durch ein differentiell kleines Flächenelement senkrecht zu den Achsen die momentane Teilchennettostromdichte j mit den folgenden Komponenten (wobei wir hier der Übersichtlichkeit halber die Zeit-Variable t weglassen):

j_x	µ	¶ n(x,y,z ) ¶x

j_y	µ	¶ n(x,y,z ) ¶y

j_z	µ	¶ n(x,y,z ) ¶z

Da der Nettostrom positiv ist, wenn er von Bereichen hoher zu niedriger Dichte fließt, was zu einer negativen ersten Ableitung der Dichte führt, kann bei den Proportionalitäten ein Minuszeichen explizit berücksichtigt werden; dies führt dazu, daß die verbleibende Proportionaltiätskonstante (als D notiert) positiv ist:

j(r;t) = – D · Ñn(r;t)

Diese Proportionaltiätskonstante D heißt Diffusionskoeffizient des Teilchens. Sie ist durch die Eigenschaften des diffundierenden Teilchens und der Art des Gitters, in dem es herumirrt, eindeutig gegeben. Für fcc- und bcc-Gitter haben wir beispielsweise

D(T) =	a² · r(T) = a² · n₀	· exp ( –	E^M k_BT	) =	D ₀ · exp ( –	E^M k_BT	)

Dabei haben wir für die Sprungrate r die Formel von oben eingesetzt. Der Vorfaktor D₀ ist offenbar a² · n₀ – und das gilt mit kleinen (und hier unwichtigen) Modifikationen für alles, was in Kristallgittern herumhüpft oder per random walk diffundiert.

Die obige Formel heißt "1. Ficksches Gesetz" nach Herrn Adolf Fick und ist eine der wichtigsten materialwissenschaftlichen Formeln der ET&IT .

Warum? Nun, wir brauchen die Diffusion von P in Si usw. nicht nur zum Herstellen von elektrotechnischen Produkten, sondern nirgendwo war gesagt, daß die diffundierenden Teilchen keine Ladung haben dürfen. Leerstellen und ZGA können geladen sein (man betrachte diese Defekte mal in einem Ionenkristall); Elektronen sind definitiv geladen – und für frei umherirrende Elektronen (wie in Metallen und Halbleitern) gilt das 1. Ficksche Gesetz auch!

In diesem Fall wird durch einen Teilchendiffusionsstrom j_Diff immer auch Ladung transportiert: Die Einheit ist jetzt [j_Diff ] = C/(cm² · s) = A/cm², und dies ist eine elektrische Stromdichte!

Ein elektrischer Diffusionsstrom ist ein
Strom elektrisch geladener Teilchen,
der dem 1. Fickschen Gesetz gehorcht.

In anderen Worten: Sollte irgendwo ein Dichtegradient diffusionsfähiger geladener Teilchen existieren, wird ein Diffusionsstrom und damit automatisch auch ein elektrischer Stom einsetzen.

Und der Diffusionsstrom ist kein vernachlässigbarer Minimaleffekt, sondern dominant in Halbleiterbauelementen (und vielen anderen Komponenten der Elektrotechnik).

Dichtegradienten sind aber nicht die einzige Ursache für elektrischen Strom!

Elektrische Felder E, zum Beispiel, üben Kräfte auf geladene Teilchen aus und sorgen daduch für Bewegung=Teilchenstrom=elektr. Strom. Elektrische Felder produzieren deshalb in (fast) allen Materialien eine Feldstromdichte j_Feld, die gegeben ist durch das lokale Ohmsche Gesetz in der Form

j_Feld = s· E = 1/r · E

mit s = spezifische Leitfähigkeit und r = 1/s = spezifischer Widerstand.

Mikroelektronik usw. "funktioniert" nur, weil sich die beiden Stromtypen – Diffusionsstrom und Feldstrom – ins Benehmen setzen müssen.

Dichten und 2. Ficksches Gesetz

Wir legen noch eins drauf, schauen das Bild oben an, erkennen, daß bei der Ausgangsverteilung der Phosphoratome jetzt ein Phosphoratom-Diffusionsstrom ins Innere des Si (nach rechts) fließt, und fragen uns, wie sich dadurch die Dichte n_P(x, t) der Phosphoratome in der Tiefe x im Si mit der Zeit t ändert.

Die Antwort auf diese Fragestellung gibt das 2. Ficksche Gesetz.

Das 2. Ficksche Gesetz läßt sich leicht aus dem 1. Fickschen Gesetz ableiten; wir benötigen zusätzlich nur noch die Kontinuitätsgleichung.

Zu deren Ableitung betrachten wir eindimensional ein Volumenelement des Systems und erhalten dann die lokale Änderung der lokalen Dichte aus einer Bilanzierung: Änderung = Was reinfließt minus was rausfließt – und sonst nichts (deshalb der Name Kontinuitätsgleichnung).

Wir bilanzieren wie beim Girokonto : Was wir auf dem Konto haben, ist die Differenz dessen, was zu- und was abfließt – plus das, was schon da war.

Die zeitliche Änderung der Dichte "am Ort x", dn(t)/d t, ist gegeben durch das, was bei x pro Zeiteinheit hineinfließt (= j(x)/dx), minus dem, was bei x + dx hinausfließt (= j( x + dx)/dx).

Warum jeweils die Division durch dx? Weil das, was hinein- oder herausfließt, immer gleich ist, wir aber die Dichte im gesamten Volumen "Querschnittsfläche mal dx" bilanzieren. Und je größer dieses Volumen ist, desto kleiner ist die Veränderung der Dichte durch das, was hinein- oder herausfließt.

Betrachten wir mal nur den Zustrom durch die Querschnittsfläche A, gegeben durch den Ausdruck j(x) · A. Weil dieser Ausdruck eine absolute Gesamtteilchenanzahl angibt, ändert sich die Dichte im betreffenden Volumen V folglich um j(x) · A / V. Weil hier aber V = A · dx ist, ergibt sich für die Änderung der Dichte der durch dx geteilte Ausdruck.

Damit machen wir also aus der Flächendichte, gemessen in cm^–2 (auf die sich die Stromdichte j bezieht), die Volumendichte, gemessen in cm^–3! (Wer das nicht unmittelbar nachvollziehen kann, sollte dringend die Links betätigen!)

Damit erhalten wir die eindimensionale Kontinuitätsgleichung (hier vereinfacht ohne partielle Ableitungen notiert):

dn(t) dt	=	j(x) – j(x +dx) dx	= –	dj(x ) dx

Auf drei Dimensionen erweitert, lautet die Kontinuitätsgleichung (in der abkürzenden Physiker-Schreibweise, daß die partielle Ableitung nach der Zeit durch einen Punkt oberhalb der betreffenden Größe angezeigt wird) einfach + Ñ·j = 0; hierbei bedeutet Ñ·j die Divergenz der Stromdichte, d. h. die lokale Stärke ihrer Quellen und Senken.

Setzen wir für die Stromdichte auf der rechten Seite das 1. Ficksche Gesetz ein (d. h. den Diffusionsstrom) und verwenden gleich die Erweiterung auf drei Dimensionen, erhalten wir das 2. Ficksche Gesetz – jetzt mit den partiellen Ableitungen notiert, um die wir uns zuvor gedrückt haben; dafür wurde überall das Argument (x,y,z;t ) weggelassen:

¶n ¶ t	= D ·	æ ç è	¶ ²n ¶x²	+	¶ ² n ¶y²	+	¶² n ¶z²	ö ÷ ø	= D · Dn

Das Dreieck auf der rechten Seite ist zwar der griechische Buchstabe "Delta", bedeutet hier aber keine Differenz, sondern bezeichnet den Laplace-Operator (Summe der zweiten partiellen Ableitungen nach allen drei Ortskoordinaten; in Kurzfassung: D = Ñ· Ñ). ("Mathematik ist die Wissenschaft der Abkürzungen." – Prof. H. Föll)

Das 2. Ficksche Gesetz ist also nichts anderes als die Kontinuitätsgleichung des Diffusionsstromes, d. h. sie drückt aus, daß sich beim Diffundieren die lokale Dichte nur als Netto-Effekt von Zu- und Abstrom ändert; weder entstehen lokal Teilchen aus dem Nichts, noch verschwinden sie spontan. (Nun ja: Derartige Prozesse gibt es auch, aber die lernen wir erst später kennen!)

In anderen Worten: Kennen wir die Dichteverteilung der diffundierenden Teilchen zu einem bestimmten Zeitpunkt, können wir durch Lösung der obigen Differentialgleichung das Dichteprofil der Teilchen, d.h. ihre Verteilung im Raum, für jeden beliebigen Zeitpunkt berechnen.

Das ist so etwas wie die Grundaufgabe der Halbleitertechnologie – siehe oben!

Die durch das 2. Ficksches Gesetz postulierte Differentialgleichung sieht nicht besonders schwer aus; wir wollen sie also übungsweise mal für einfache Randbedingungen lösen. Je nach der verwendeten Randbedingung ergibt sich eine reine Umverteilung aller Teilchen im Raum (bei einer "erschöpflichen Quelle" der diffundierenden Teilchen), oder es kann eine Änderung der Gesamtteilchenzahl eintreten, wenn ein externer Zu- oder Abstrom vorhanden ist ("unerschöpfliche Quelle/Senke").

Übungsaufgabe
Aufgabe 4.2-2

Wer die Übung gemacht hat, weiß, daß das 2. Ficksche Gesetz trickreicher ist, als man auf Anhieb denkt! Selbst einfache Situation haben Lösungen, in denen Gaußverteilungen oder "error functions" vorkommen; d.h. mathematische Formeln aus der Stochastik. Warum auch nicht – die Differentialgleichung beschreibt ja ein statistisches Phänomen – völlig regelloses Herumgehüpfe!

Wir wollen deshalb an dieser Stelle aufhören und im nächsten Unterkapitel nur noch eine schnelle Konsequenz der Diffusion anschauen, die mit einer sehr einfachen Formel verbunden ist.

Fragebogen
Schelle Fragen zu 4.2.2

¹⁾ Keine Regel ohne Ausnahmen. Bei der sogenannten "Neutron transmutation doping"-Technik werden substitutionelle Phosphoratome im Si dadurch erzeugt, daß man den Si-Kristall für einige Zeit in einen Kernreaktor hängt; durch die dort vorhanden Neutronen werden Si-Atome in P-Atome umgewandelt ("transmutated"). Obwohl das etwas abwegig scheinen mag, handelt es sich um eine etablierte und benutzte Technik.