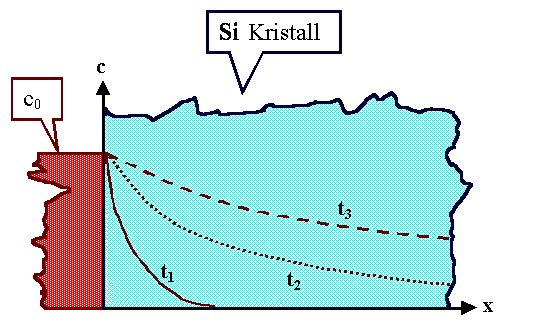
 |
Wir betrachten ein eindimensionales Problem: Ein Stück Si hat bei
x = 0 auf der Oberfläche ein konstante und unerschöpfliche Dichte n¥
an Arsenatomen; im Inneren liege die konstante Dichte n0 << n¥
vor. |
|
 |
Damit haben wir eine Rand- und Anfangsbedingung gegeben. |
|
Die Arsenatome (oder Phosphor-, Boratome) diffundieren im Laufe der Zeit ins Silizium;
wir können vermuten, dass sich Konzentrationsprofile wie gezeichnet einstellen werden. |
| |
|
|
|
Wer mag, liest erst mal nicht weiter, sondern schaut mal, wie weit sie bei der Berechnung
der Diffusionprofile kommt - das Problem ist zusammen mit dem 2. Fickschen Gesetz eindeutig gegeben und lösbar. |
|
| |
|
|
|
Der Rest zeigt, dass der folgende Ausdruck die gesuchte Lösung ist: |
| |
| n(x, t) = (n¥ –
n0) · | æ
ç
è
| 1 – erf |
æ
ç
è |
x
2(D · t)1/2 |
ö
÷
ø |
ö
÷
ø |
+ n0 |
|
|
|
|
Der Ausdruck "erf " steht dabei für
"Errorfunction
" oder Gaußsche
Fehlerfunktion; eine tabellierte Funktion mit folgender Definition: |
| |
| erf (x) = | 2
p1/2 | · |
x
ó
õ
0 | exp – x'
2 · dx' |
|
|
|
|
Daß bei der Lösung der Diffusionsgleichungen,
wie die Fickschen Gesetze auch genannt werden, typische Funktionen der Statistik auftreten, ist eigentlich für uns
nicht überraschend, denn wir haben schließlich rein statistische Bewegungen der Teilchen als Grundprozeß. |
|
|
Dass die Differentialgleichungen der Fickschen Gesetze dann doch nicht so ganz einfach zu
lösen sind - that's life! |
|
Hier noch ein paar nützliche Hinweise: |
| |
|
© H. Föll (MaWi für ET&IT - Script)
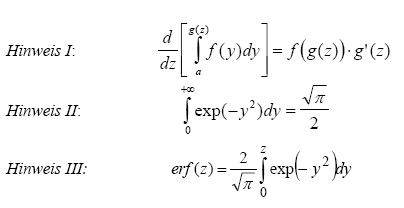
4.2.2 Diffusion mit atomaren Fehlstellen und Ficksche Gesetze 
Mit Frame