2.1.3 Bindungspotentiale und weitere Eigenschaften

Kristallbilder = abstrakte Symbolik

	Wir haben jetzt ein schematisches Bild eines Kristalls, das etwa so aussieht:
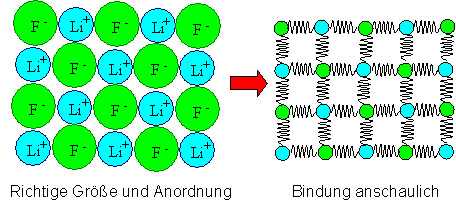
		Links ist das zweidimensionale Bild eines LiF-Kristalls mit halbwegs richtigen Größenverhältnissen der Ionen und in der richtigen ("kubischen") Anordnung. Rechts ist eine Darstellung, in der die Bindung zwischen nächsten Nachbarn durch eine Feder dargestellt ist, die das Bindungpotential symbolisiert. Man sieht nicht mehr die Größenverhältnisse und daß die Ionen"kugeln" sich berühren, dafür aber die kubische Struktur eher besser.
		Was man nicht sieht, sind die Federn = Bindungspotentiale zu den zweitnächsten Nachbarn usw., die aber sowohl da sind als auch gebraucht werden.
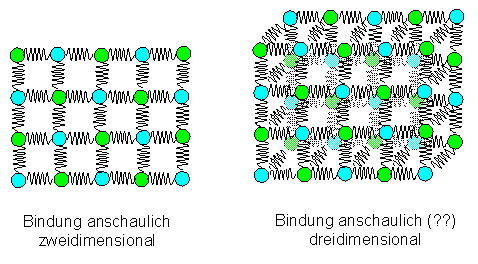
		In einer dreidimensionalen (perspektivischen Darstellung) würde man nicht mehr viel sehen, außer ...
		... daß zumindest zwischen den zweitnächsten Nachbarn (Diagonalen) noch "Federn" gebraucht werden, denn das Kugeln-Federn-Paket von oben rechts würde, so wie es gezeichnet ist, bei "weichen" Federn sofort kollabieren.
	In der nächsten Abstraktionsebene zeichnen wir der Einfachheit halber einige der (niemals alle) Bindungsfedern zwischen den nächsten Nachbarn als Striche. Ein Beispiel:
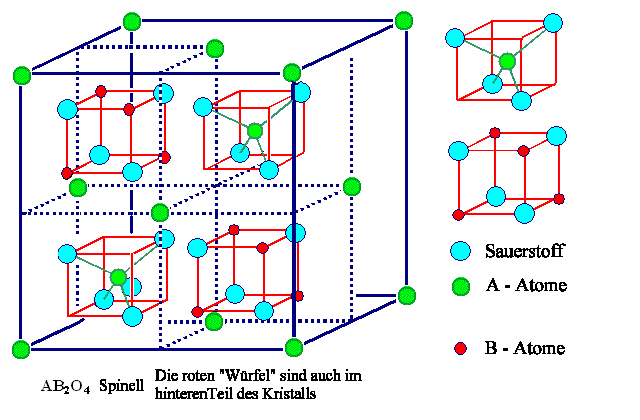		Das Mineral "Spinell" hat die Bruttoformel Mg2+(Al3+)2 (O2-)4. Die Welt ist voll von Kristallen dieser Art.
		Wichtig ist nur zu kapieren, daß Bildchen dieser Art immer sehr abstrakt sind und immer mehr oder weniger "falsch". Aber – es geht nicht anders.
	Es kommt noch schlimmer: In jedem der Bilder sitzen die Symbole für die Atome bzw. Ionen fest auf einem "Gitterplatz". Das ist allenfalls am absoluten Nullpunkt richtig.
		Bei endlichen Temperaturen (unterhalb des Schmelzpunktes) enthält unser Kristall thermische Energie. Die Frage ist: Wie äußert sich diese thermische Energie in den Bildchen und den Bindungspotentialen?

	Thermische Energie eines Kristalls
	Bitte jetzt verinnerlichen:
		Temperatur ist ein Maß für die einem Körper innewohnende ungeordnete (genauer: statistisch verteilte) (Bewegungs-)Energie. Temperaturänderungen erfordern Energiezufuhr oder -abfuhr.
		In einem Kristall bei der Temperatur T2 > T1 steckt mehr thermische Energie als bei T1. Wo ist diese thermische Energie?
		Nebenbei: In einem Kristall, der mit der Geschwindigkeit v2 Auto fährt und die Temperatur T1 hat, steckt zwar mehr (geordnete) kinetische Energie ½mv 22 als in einem Kristall bei v1 < v2 und T1, aber dieselbe ungeordnete thermische Energie. (Und ganz bewußt wird hier von "thermischer Energie" gesprochen und nicht von "Wärme", denn Energie ist eine Zustandsgröße, Wärme dagegen eine Prozeßgröße . Was das genau bedeutet, erfahren wir später.)
	Es gibt nur eine mögliche Antwort auf die obige Frage: Die thermische Energie der Kristalle steckt in Vibrationen der Atome, d.h. in den Schwingungen der Atome um ihre Gleichgewichtslage! Je heißer, desto mehr wackelt's!
		Wenn man das Federbild oben anschaut, kann man sich das leicht vorstellen. Gibt man Energie in das Masse-Federn-System, wird ein wildes Oszillieren stattfinden. Ein herausgegriffenes Atom wird mal mit großer, mal mit kleiner Amplitude; mal in diese, dann in jene Richtung schwingen. Keine Chance, dem individuell zu folgen.
		Wollen wir aber auch nicht, Mittelwerte reichen.
	Wir nehmen jetzt mal eine extrem einfache und gleichzeitig sehr allgemeine Definition der Temperatur zur Kenntnis:
		Bei der (absoluten) Temperatur T hat ein Teilchen in einem Teilchensystem (Kristall, Gas, ...), das sich im thermodynamischen Gleichgewicht befindet*, im Mittel die thermische Energie (innere Energie) UTeilchen = ½f kBT bei f Freiheitsgraden der Energiespeicherung. (*: Sobald man das Wort "Temperatur" in den Mund genommen hat, spricht man automatisch von einem System, das sich im thermodynamischen Gleichgewicht befindet!)
		Die "Freiheitsgrade" zählen schlicht ab, auf wieviel Arten man Energie "speichern" könnte. In einem Kristall gibt es sechs. Na ja, eigentlich haben die Atome in einem Kristall, rein kinematisch betrachtet, nur drei unabhängige Bewegungsmöglichkeiten, aber die zählen, weil es bei den Freiheitsgraden um die gesamte thermische Energie geht, doppelt: Je drei für die mittleren kinetische Energie der Schwingung in x -, y- und z-Richtung, und je drei für die Erhöhung der mittleren potentiellen Energie durch Abweichungen von der Ruhelage im Potentialtopf des Atoms in seiner Bindungsumgebung. (Diese "energetische Doppeltzählung" gilt übrigens auch für Schwingungen innerhalb eines mehratomigen Moleküls!)
	Das ist aber hier nicht gar nicht so wichtig. Wir lernen nur: Temperatur = Schwingungen um die Ruhelage. UTeilchen » Etherm = kBT reicht für unsere Zwecke völlig aus
		Dies ist eine der wenigen Formel, die man wissen muss. Sie definiert, was Temperatur eigentlich ist, und erlaubt abzuschätzen, was bei gegebener Temperatur energetisch passieren kann.
		Was können wir daraus für Schlüsse ziehen? Schauen wir uns das einfach mal im Potentialtopfmodell für zwei Temperaturen an, wobei T2 > T1 ist:
		Falls die Atome um ihre Gleichgewichtslage schwingen, wird der Abstand zwischen den Bindungspartnern periodisch kleiner und größer. Beim jeweiligen Extremum des Abstands – größte oder kleinste Entfernung, r max bzw. rmin – ist die Energie der Oszillation reine potentielle Energie, eben exakt die Energie, die das Potential für den jeweiligen Anstand r vorgibt.
		Beim Nulldurchgang ist die Energie rein kinetisch. Immer jedoch ist die Gesamtenergie E, die Summe aus potentieller und kinetischer Energie, konstant.
	Achtung! Wir erlauben uns hier den Luxus, ein-und-denselben Buchstaben E sowohl für die Gesamtenergie als auch für den E-Modul (und später noch für das elektrische Feld) zu benutzen! Aus dem jeweiligen Kontext heraus gibt es eigentlich keine Verwechslungsgefahr. Im Notfall verwenden wir nicht Indizes, griechische, altdeutsche oder andere Symbole, sondern – wir sind modern – Farbe.
		Damit können wir die Oszillationen der Bindungspartner als Energieniveau in den Potentialtopf des Bindungspotentials einzeichnen. Jedes denkbar Niveau ist erlaubt, da die Oszillation jede Amplitude haben kann.

	Frequenz der Gitterschwingungen und thermischer Ausdehnungskoeffizient
	Zunächst sind zwei Fragen zu beantworten: Wie groß ist die Frequenz n der Schwingungen? ("n " ist der griechische Kleinbuchstabe "ny".) Wo ist das oszillierende Atom im Mittel?
		Wer die Übungsaufgabe im Modul 2.1.2 gemacht hat kennt die Antwort – zumindest der Spur nach. Wer's nicht gemacht hat, macht's jetzt – für die Frequenz!
		Übungsaufgabe Aufgabe 2.1-3
	Das Ergebnis ist: Die Schwingungsfrequenz von Atomen in einem Kristall (Festkörper) liegt in der Größenordnung n = 1013 Hz. Das ist eine Zahl, die man wissen muss.
		Als Elektro- und Informationstechniker fragen wir uns jetzt automatisch, wo wir dieses Frequenzband einzuordnen haben, und was für eine Bedeutung dieses "Eigenschwingverhalten" der Materie dann hat.
		Im "einfachen Frageteil" der Übungsaufgaben wird dazu gezielt gefragt; hier nehmen wir nur mal zur Kenntnis, daß wir später darauf zurückkommen werden.
	Jedenfalls haben wir jetzt bereits zwei weitere wichtige und ganz allgemeine Eigenschaften der Festkörper aus dem Bindungspotential gewonnen:
		Die Vibrationsfrequenz der Gitterschwingungen n » 1013 Hz Den thermischen Ausdehnungskoeffizienten a =  l (T)   –  l0 l0 · T  =  etherm T
	???? Wo kommt der thermische Ausdehnungskoeffizent her? Und wieso "haben" wir ihn? Nachdem wir bisher alles sehr ausführlich dargestellt haben, drücken wir jetzt mal ein bißchen auf's Gas.
		Im obigen Bild war schon eingezeichnet, daß sich der mittlere Abstand mit zunehmender Temperatur vergrößert – wir haben thermische Ausdehnung! Es ist vom Bild her auch schon klar, daß der Effekt um so größer sein wird, je asymmetrischer das Bindungpotential ist.
		Die Frage ist, können wir die relevante Kurve, die durch die Mitte der Energieveaus geht, aus dem Bindungspotential berechnen? Die Antwort ist: ja – aber nur mit großer Mühe; hier ist ein einschlägiger Link.
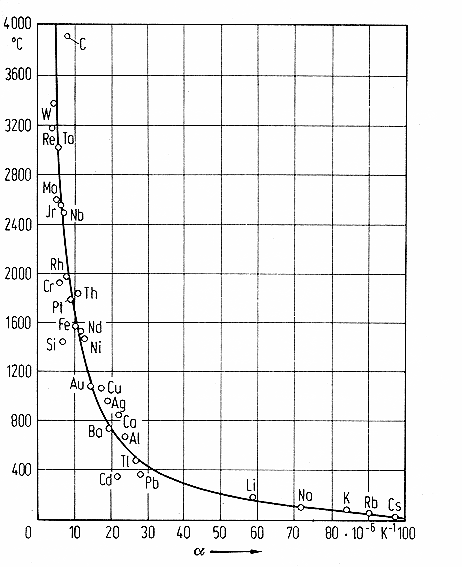
		Was rauskommt, sieht so aus:
		a =  n + m + 3  =  const.  ·   1  2 · n · m · U0 T m
		Die Graphik zeigt, daß man damit nicht schlecht liegt. Bitte mal kurz nachdenken: Die Graphik war schon lange vor der Formel bekannt. Was wir hier getan haben, ist nichts Geringeres, als eine fundamentale Eigenschaft der Materie aus sehr grundlegenden Erwägungen heraus zu verstehen!
	Gehen wir direkt zur nächsten fundamentalen Eigenschaft:

	Maximale Bruchdehnung
	Wer die Übungsaufgabe gemacht hat, ist eigentlich schon fertig
		Hier ist ein Ergebnis:
	Wir sehen, daß wir mit einem gewissen Kraftaufwand (blaue Kurve) die Bindungspartner auseinanderziehen können. Die notwendige Kraft erreicht aber ein Maximum am (rechten) Wendepunkt der Potentialkurve!
		Das bedeutet, daß wir mit einer Kraft FBruch (oder besser, auf die Fläche bezogen, einer Spannung sBruch), die unwesentlich größer ist als die max. Kraft, den Abstand ® ¥ treiben. In anderen Worten: Die Bindungen und damit der Körper brechen auseinander.
		Die maximale Bruchspannung sBruch sowie die zugehörige Bruchdehnung eBruch = (r Wendepkt – r0)/r0 ergibt sich damit eindeutig aus dem Bindungspotential. Nach wiederum ziemlich langer und öder Rechnung erhält man
		sBruch =  n · m · U0 r03 æ ç è æ ç è n + 1 ö ÷ ø 1/(n – m)   –  1 ö ÷ ø m + 1 eBruch  · 100 <»  30 %
	Es folgt jetzt keine Vereinfachung oder eine Graphik zum Vergleich mit experimentellen Werten, denn:
		Die Formel stimmt nicht mit dem Experiment überein!
	Wie kann das sein? Haben wir einen Fehler gemacht? Nein, haben wir nicht – aber:
		Wir haben, ohne groß nachzudenken, einen idealen, zu 100 % perfekten Kristall unterstellt. Solche Kristalle gibt es nicht!
		Reale Kristalle, die immer irgendwelche Defekte enthalten, brechen immer bei viel kleineren Bruchspannungen! Wir dagegen haben das ultimative Maximum ausgerechnet; darüber geht schlicht nichts mehr.
	Sch....! Das hat eine Reihe von Konsequenzen: Reale Materialien brechen früher als sie müßten. Nicht gut für technische Zwecke! Bei welcher Belastung sie brechen, hängt offenbar von Defekten ab. Das sind aber gerade die nicht so leicht zu fassenden Strukturmerkmale eines Materials. In anderen Worten: Die Bruchfestigkeit eines gegebenen Materials ist keine Konstante. Nicht gut für technische Zwecke! Daß Eigenschaften defektabhängig sind, soll ja auch sonst oft gelten. Wir müssen uns also mit der komplexen Materie "Defekte in Kristallen" befassen!
		Trotzdem haben wir eines gelernt: Falls wir nach ultrafesten Materialen suchen sollten, ist das "Tüfteln" in der Garage ziemlich sinnlos. Man tut besser daran, über Bindungspotentiale das maximal Mögliche zu ermitteln, und dann mit "defect engineering" dem Maximum möglichst nahe zu kommen.
	Wir haben jetzt 5 Materialeigenschaften ziemlich direkt mit dem Bindungspotential korreliert oder sogar quantitativ abgeleitet: Schmelzpunkt Elastizitätsmodul Frequenz der Schwingungen Thermischer Ausdehnungskoeffizient Maximale Bruchspannung und -dehnung
		Das mögen ja ganz interessante Eigenschaften sein, aber nicht so sehr für Ingenieure der Elektrotechnik und Informationstechnik. Schon wahr, aber der Weg zu den elektrisch interessanten Eigenschaften führt auch über Bindungspotentiale – wir werden sehen!
	Um auf diesem Weg weiterzukommen, schauen wir uns jetzt die letzte aus Bindungspotentialen resultierende Eigenschaft an: Die Bildung von Kristallen.
	Um sicher zu sein, daß alles sitzt, machen wir noch die folgenden einfachen Übungen:
		Übungsaufgabe Aufgabe 2.1-3
		Fragebogen Einfache Fragen zu 2.1.3
		Fragebogen "Multiple Choice"-Fragen zu 2.1

© H. Föll (MaWi für ET&IT - Script)