2.4.2 Thermischer Ausdehnungskoeffizient

Problemstellung

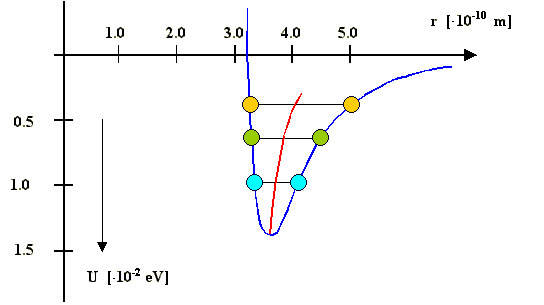
	Wir betrachten jetzt mal einen "echten" und damit immer asymmetrischen Potentialtopf, z.B. von einem Kr- Kristall.
		Ein beliebig herausgegriffenes Atom schwingt zwischen den eingezeichneten Extrempositionen hin und her; bei höheren Temperaturen, kann es höher den Potentialtopf hinauflaufen (z.B. bis zu den orangen Kreisen)
		In einem asymmetrischen Potentialtopf wie in dem Bild (es handelt sich um das sehr schwache Bindungspotential eines Kr Kristalls, wird das Atom länger rechts von der Mitte als links von der Mitte sein; der mittlere Atomabstand als Funktion der Schwingungsamplitude wird auf der roten Linie liegen
	Wie berechnet man daraus den (linearen) thermischen Ausdehnungskoeffizienten a? Zunächst brauchen wir eine Definition:
		Der (lineare) thermischen Ausdehnungskoeffizienten ist definiert als
		a  =  l (T)   –  l0 l0 · T  =   etherm T
		In Worten: a = thermische Dehnung etherm pro Grad Kelvin; die Dimension von a ist K–1
	Wenn wir die Amplitude der Schwingung und die beiden Extremalpositionen berechnen wollen, müssen wir die folgende Gleichung lösen.
	U = 3/2kT  =  –   A   rexn  +  B   rexm
		Denn die Energie an einer der durch farbige Kreise markierten Extremalpositionen rex ist gleich der mittleren thermischen Energie und die ist ½ kT pro Freiheitsgrad; also 3/2 kT für die drei Freiheitsgrade der Schwingungen in den drei Koordinatenrichtungen.
		Das ist jetzt zwar im Grunde nur noch "triviale" Mathematik - eine Gleichung mit einer Unbekannten - aber leider gibt es keine allgemeinen Lösungen für Gleichungen n-ten oder m-ten Grades mit m oder n > 4.
	Das war's also - für exakte allgemeine Lösungen. Entweder löst man numerisch, oder man muß für gegebene m, n versuchen eine Lösung zu finden.
		Was bleibt sind Näherungslösungen. Wir werden, auf einem recht trickreichen Weg, jetzt eine sehr einfache solche Näherungslösung vornehmen.

Näherungsweise Lösung

	Zunächst machen wir eine mathematische Näherung und beschreiben die Potentialformel durch eine Potenzreihenentwicklung (Taylor Reihe) um das Minimum, d.h. für r = r0. Wir erhalten:
		U  =  U0 + 1/2U0''  · x2 + 1/6U0'''  · x3 + ....
		Mit U0''  = d2U/dr2 = zweite Ableitung nach r; U0''  =dritte Ableitung nach r.
		Die Reihenentwicklung verschiebt den Nullpunkt auf das Potentialminimum, oder, in anderen Worten, wir haben x = r – r0.
		Die erste Ableitung ist im Potentialminimum = 0, höhere Ableitungen als die dritte vernachlässigen wir. Die dritte Ableitung aber ist essentiell: Sie enthält die Asymmetrie des Potentials, die ja erst für die thermische Ausdehnung sorgt.
	Die erste Ableitung sollte im Rahmen einer Übungsaufgabe ausgerechnet werden, sie ist (siehe Lösung)
		dU dr  =  U' = n · A · r–(n + 1) – m · B · r–(m + 1)
		Auch die zweite Ableitung ist in der Lösung der Aufgabe 2.4-1 enthalten, wir haben (etwas umgeschrieben)
		d2U dr 2  =  U''  =  – n · (n + 1) r 2  · A · r –n  +   m · (m + 1) r 2  · B · r –m
		Wir brauchen U'' nur im Potentialminimum; setzen wir also r  =  r0 und berücksichtigen daß U'(r0) = 0; wir erhielten
		U''(r0)  = U0 ·  nm r0 2
		Die dritte Ableitung ist damit .
		d3U dr 3  =  U'''   = – n · (n + 1) · (n + 2) r 3 · A · r –n  +   m · (m + 1) · (m + 2) r 3 · B · r –m
		Oder, wieder für r  = r0,
		U'''(r0)  =  – U0 ·   n · m · (n + m + 3) r0 3
	Damit lautet die Näherungsformel für das Bindungspotential in der Nähe des Potentialminimums
		U(r0+x)  =  U0 · æ ç è 1  +  n · m · x2  –    n · m · (n + m + 3) · x3 ö ÷ ø 2 · r02 6 · r03
		Für die Amplitude eines Atoms das in diesem Potential schwingt betrachten wir den Wert der Funktion bei der Energie U0 + (3/2) kT, wir haben also eine implizite Gleichung für die (jeweils halbe) Amplitude x
		(3/2) kT  =   æ ç è n · m · x2  –    n · m · (n + m + 3) · x3 ö ÷ ø 2 ·r02 6 ·r03
	Wir haben jetzt eine Gleichung dritten Grades für die Extremwerte von x für eine gegebene thermische Energie; und diese Gleichung können wir im Prinzip lösen.
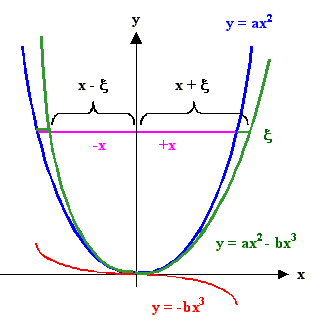
		Was herauskommt wird aber ziemlich länglich sein. Also gehen wir anders vor: Wir betrachten die beiden relevanten x-Werte als eine kleine Korrektur der Werte ± x(T) die wir für ein schlichtes parabelförmiges Potential bekommen würden (die dann natürlich keine thermische Ausdehnung enthalten):
		(3/2) kT  =   æ ç è n · m · x2 ö ÷ ø 2 ·r02
		Die Lösungen der quadratischen Gleichung können wir sofort hinschreiben; wir haben x1,2 = Amplitude nach links; rechts = ±{3k·T·r02/n·m}½ = {3kT/U''}½ = ± x0. Die beiden letzten Terme sind nur Umschreibungen um im folgenden Schreibarbeit zu sparen.
	Wir machen damit jezt folgenden Ansatz für die Lösung der kubischen Geichung:
		Amplitude nach links = –x0 + x, Amplitude nach rechts = +x0 + x.
		Was das genau bedeutet ist in der Zeichnung dargestellt (die im übrigen klarmacht, daß die Beschreibung mit einer Kurve dritter Ordnung einer leicht gekippten Parabel entspricht).
	Einsetzen in die Gleichung dritten Grades und ausmultiplizieren gibt eine Bestimmungsgleichung dritten Grades für x; und x ist natürlich genau die Abweichung von der Gleichgewichtsposition:
		x  =  r  –  r0  =  etherm · r0
		Damit hätte man das Problem innerhalb der mathematischen Näherung mit einer Taylor Entwicklung exakt gelöst - aber noch nichts gewonnen; wir haben immer noch eine Gleichung dritten Grades. Wir können jetzt aber berücksichtigen, daß die thermische Ausdehnung generell ein kleiner Effekt ist, und das heißt, daß sowohl x klein ist gegenüber x0, als auch daß |U'''| klein ist gegenüber |U''|.
		Wir machen jetzt eine physikalische Näherung und vernachlässigen einfach alle mindest "quadratisch kleinen" Terme, also alle x2, x3 und - wir sind radikal - alle Produkte zwischen x und U'''.
	Damit bekommen wir (aus schreibtechnischen Gründen wieder mit den Ableitungen ausgedrückt)
		(3/2) kT = (1/2) ·U0''  · (x0 + x)2 + 1/6U0'''  · (x0 + x)3 = (1/2) · U0''  · {x02 + 2 ·x0 · x} + 1/6U0'''  · {x03}
		Setzen wir den Wert für x02 ein, heben sich die beiden ersten Terme auf; ein x0 kürzt sich heraus, und es bleibt
		0  =  x · U0''  + 3kT · U0''' 6U''
		Damit ergibt sich für x:
		x  =  –  kT · U0''' 2(U'')2
	Wir brauchen nur noch die Werte für die Ableitungen von oben einsetzen, uns daran erinnern, daß für den thermischen Ausdehnungskoeffizient a gilt:
		a  =   etherm  =  x T r0 · T
		Damit erhalten wir die Endformel
		a  = –  kT · U0'''  =  –   {–U0 · [n · m · (n + m + 3)/r03]} · kT 2(U'')2 · r0 · T 2r0 · T · {U0 · (n · m/r02)}2
	Das meiste kürzt sich heraus; was bleibt ist sehr einfach
		a  =  (n + m + 3)k 2 · n · m · U0
	Kleinere Erschöpfungszustände an dieser Stelle sind normal - immerhin zeigt sich, daß all die Zeit, die man im Gymnasium mit Bruchrechnen, Gleichungen lösen und Polynome ableiten verbracht hat, zu etwas gut war. Aber wir sind noch nicht fertig.
		Wir sehen, daß a umgekehrt proportional zur Bindungsenergie U0 ist. Wir wissen aber, daß der Schmelzpunkt Tm ungefähr proportional zu U0 ist - in der einfachsten Näherung, die wir für die Faustformel des E-Moduls verwendet haben, setzten wir U0 = kTm.
		Eingesetzt in die Formel für a ergibt sich dann ein direkter Zusammenhang zwischen dem Schmelzpunkt und dem thermischen Ausdehnungskoeffizienten:
		a  =  n + m + 3  =  const.  ·   1 2 · n · m · Tm Tm
	Das ist eine Beziehung, die man leicht überprüfen kann. Die Graphik (aus dem "Hornbogen") zeigt das Ergebnis
		Für praktisch alle Metalle ergibt sich eine hervorragende Übereinstimmung - die Werte liegen fast alle sehr gut auf der erwarteten Hyperbel, bei einem Schmelzpunktintervall von mehr als 3 000 K!

© H. Föll (MaWi 1 Skript)