2.1.2 Bindungspotentiale, Federn und Elastizitätsmodul

Potential einer Feder und Federkonstante

	Wir beginnen diesen Modul mit einer Aufgabe zu einer idealen Feder, die man unbedingt machen, aber auf jeden Fall ansehen und nachvollziehen sollte (Lösung vorhanden)!
		Übungsaufgabe Aufgabe 2.1-1
	Dann schauen wir uns mal einen simplen Versuch an: Wir ziehen eine Feder lang. Wir nehmen aber keine Sprungfeder (technisch korrekt: Schraubenfeder), sondern der Einfachheit halber nur einen zylindrischen Draht.
		Falls wir eine Sprungfeder nehmen würden, hätte die Feder eine Länge lFed, der Draht, aus dem sie gewickelt ist, aber eine viel größere Länge lDra. Zieht man die Feder um ein DlFed lang, verlängert sich der Draht selbst nur um DlDra » DlFed · (lFed / lDra); außerdem wird er auch noch tordiert (= verdrillt).
		Das ist uns zu kompliziert, wir ziehen deshalb gleich an einem geraden Draht der Ausgangslänge l0.
		Je nach angelegter Kraft F wird der Draht um ein Dl länger werden, und wir können eine "Federkonstante" kFed = F/Dl definieren. Wenn wir einen dickeren oder kürzeren Draht aus demselben Material nehmen oder den Draht jetzt wickeln, resultieren jeweils andere "Federkonstanten".
	Das Verhalten des Materials gegenüber mechanischer Belastung ist aber eine Materialeigenschaft, die man sinnvollerweise mit einer einzigen Zahl beschreibt. Dazu müssen wir uns von den Dimensionen unabhängig machen und zu spezifischen Größen übergehen; exakt so wie vom Widerstand eines Materials (gemessen in W) zum spezifischen Widerstand. (gemessen in Wcm).
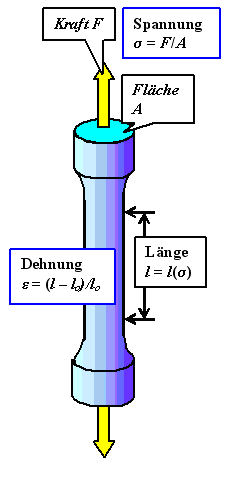
		Das machen wir zunächst durch zwei simple Definitionen anhand der unten schematisch dargestellten Geometrie bei einem Zugversuch.
		Nebenbei nehmen wir schon mal zur Kenntnis, dass der Zugversuch das paradigmatische Experiment zur Bestimmung der "mechanischen" Eigenschaften aller Festkörper ist!
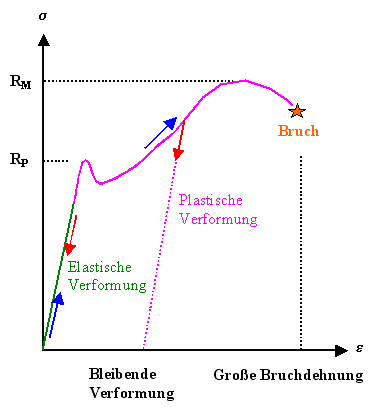
	Was man bei einem duktilen = plastisch verformbaren Material typischerweise findet ist in dem Spannungs-Dehnungs-Diagramm rechts gezeigt. Nach einem rein elastischen Bereich kommt vor dem endgültigen Bruch noch ein duktiler Bereich. Wir interessieren uns hier aber nur für den elastischen Bereich.

	E-Modul statt Federkonstante
	Für eine gegebene Kraft wird die Längenänderung Dl bei einem "dicken" Körper mit großer Querschnittsfläche A kleiner sein, als bei einem schlanken Körper desselben Materials.
		Um dieselbe Längenänderung Dl zu erreichen muß man offenbar dieselbe mechanische Spannung s  anlegen, d.h. dieselbe Kraft pro Fläche. Damit ist mechanische Spannung definiert als
		s  =  F A
		Wir werden zukünftig immer s  verwenden und bei mechanischen Problemen nicht mehr von Kräften sondern von (mechanischen) Spannungen reden.
		Die Maßeinheit für mechanische Spannungen ist das Pascal ; abgekürzt Pa. Ein Pascal ist definiert als 1 Pa = 1N/m2 = 1 Newton pro Quadratmeter.
		Man könnte das natürlich mit der elektrischen Spannung verwechseln, aber aus dem Kontext ist auch ohne das Adjektiv "mechanisch" praktisch immer klar um was es geht.
	Da auch ein langer Körper bei derselben Spannung eine größere Längenänderung zeigen wird als ein kurzer, ist es zweckmäßig auch die Längenänderung so zu normieren, daß sie von der Ausgangslänge des Probenkörpers unabhängig wird.
		Dies wird durch die Definition der Dehnung e  erreicht:
		e(s)  =  Dl  l  =  l(s)  –  l0 l0  =  l (s)  l0  –  1
		l(s) ist dabei die jeweilige von der Spannung abhängige Länge; l0 ist die Ausgangslänge für s = 0.
		Die Dehnung hat in dieser Definition keine Maßeinheit, sie ist dimensionslos. Multipliziert man den Zahlenwert mit 100, hat man die Verlängerung des Körpers in Prozent %. ("%" ist übrigens keine Maßeinheit!)
	Damit läßt sich für Körper mit konstantem Querschnitt verallgemeinern: Bei gleicher Spannung wird immer die gleiche Dehnung auftreten, unabhängig von den Dimensionen des Körpers.
		Gleiche Spannung produziert gleiche Dehnung
		Macht man einen realen Zugversuch, findet man im linearen elastischen Bereich eine eindeutige Beziehung zwischen s und e, d.h. s = s(e).
		Elastischer Bereich heißt, daß für jeden Wert von s sich immer der gleiche Wert von e einstellt. Dies bedeutet insbesondere, daß bei Wegnehmen der Spannung, der Körper wieder seine ursprüngliche Länge hat.
		Dies muß nicht so sein; wer schon mal sein Auto gegen ein Hindernis gefahren hat weiß, daß es auch inelastische oder plastische Dehnungen gibt - nach Wegnehmen der mechanischen Spannungen ist die alte Form nicht wieder hergestellt! Im Link kann man einen Großversuch zu nichtelastischen Verformungen bewundern (inkl. Brüche und Flüche).
		Für den elastischen Bereich einer s-e -Kurve läßt sich jedoch als Materialkonstante der (nicht "das") Elastizitätsmodul E (kurz E-Modul) definieren als
		E  =  ds de
	Der E-Modul wird uns noch hinreichend beschäftigen. In Kürze deshalb nur einige wichtige Punkte: Die Maßeinheit des E-Moduls ist [N/m2] oder Pascal [Pa], d. h. sie ist identisch zu der Maßeinheit der Spannung. Werte liegen maximal um 103 GPa für sehr harte Materialien (Diamant, Keramik), um 102 GPa und darunter für normale Metalle ("Stahl"), und um 1 GPa bis herunter zu 10–2 GPa für weiche Materialien (Holz - Styropor, Gummi). Mehr dazu im Link. Der E-Modul von Mixturen (Stahlbeton; Faserverstärkte Kunststoffe,..) ist eine Art Mittelwert des E-Moduls der Komponenten. Der E-Modul wird bei den elektrischen Eigenschaften der Dielektrika noch wichtig werden!
	Was ist nun der Zusammenhang zwischen der "effektiven Federkonstranten" kFed einer Bindung und dem E-Modul des Materials?
		Das ist so einfach, dass wir es in einer schnellen Übung tun.
		Heraus kommt kFed = E · r0 mit r0 = Bindungsabstand oder ungefähr "Gitterkonstante" (was das ist, lernen wir später; auch dieses Ergebnis leiten wir weiter unten ausführlich her).

	Mikroskopische Betrachtung des E-Moduls
	Wir machen jetzt etwas sehr Wichtiges: Wir setzen uns eine virtuelle Brille auf, mit der wir unter extrem hoher Vergößerung in Materialien hineinschauen können. Solche "Brillen" gibt's auch real, man nennt sie "Hochauflösungstransmissionselektronenmikroskope " (HRTEM); im Kieler Nanolabor steht eines herum.
		Virtuell kommt's aber deutlich billiger; wir sparen so um die 2 Mio €. Wenn wir mit unserer virtuellen HRTEM-Brille unserem (kristallinen) Prüfkörper beim Langgezogenwerden zuschauen, sehen wir dies (Hinweis: "Sehen" tun wir mit dem Gehirn, nicht mit den Augen):
	Wir sehen: Beim Zugversuch (im elastischen Bereich) ziehen wir (bei allen Kristallen und den meisten amorphen Materialien) schlicht und ergreifend die Bindungen in Zugrichtung "lang".
		Das ist eine monumentale Erkenntnis! Wir haben eine erste nicht-triviale Eigenschaft von Materialien auf fundamentale Parameter – die Bindungen – zurückgeführt (wenigstens im Prinzip).
	Jetzt berechnen wir mal schnell den E-Modul aus dem als bekannt vorausgesetzten Bindungspotential, und zwar im linearen Bereich (d. h. für kleine elastische Verformungen). Dazu setzen wir die Querschnittsfläche der Zugprobe auf r02 (r0 ist der Abstand zwischen den Atomen oder die "Gitterkonstante" unseres [kubischen] Kristalls). Mit andern Worten: Wir ziehen nur eine Bindung lang!
		Darf man das? – Wer sollte es verbieten? Der gesamte Effekt beim Langziehen einer Probe ist schließlich nur die Summe der Effekte der Bindungen. Man kann es übrigens heutzutage sogar experimentell machen!

	Um den Abstand eines Atoms in irgendeiner Anordnung mit Bindungsabstand r0 zu seinen Nachbarn zu ändern, muß eine Kraft FAtom angreifen, die dann auf die für das Atom (im Kristall) spezifische Fläche A = r02 wirkt.
		Die auf ein Atom bezogene Spannung s = F/A ist damit
		s  =   FAtom   r02
		Der Abstand zu den Nachbarn wird sich ändern, die zugehörige Dehnung e (in Zugrichtung) ist
		e(s)  =  r(s)  –  r0 r0
		Die Kraft FAtom , um gegen das Bindungspotential das Atom zum Ort r zu bringen, ist direkt durch die Ableitung des Potentials U(r) gegeben, wir haben FAtom = +dU(r)/d r.
		Wir haben jetzt ein Plus- anstelle eines Minuszeichens, denn wir betrachten jetzt die äußere Kraft, die gegen die rücktreibende Kraft des Potentials "arbeitet" (Zugversuch!).
	Der E-Modul E war definiert als
		E  =  ds de  =  d[FAtom/r02] de
	wobei wir für kleine elastische Verformungen die Ableitung dann natürlich an der Stelle e = 0 (das entspricht r = r0) nehmen müssen.
		Setzt man alle Beziehungen von oben ein, berücksichtigt die Kettenregel
		dFAtom de  =  dFAtom dr  ·  dr de
		und berechnet dr/de = r0, erhält man
		E  =  1    r02  ·  dFAtom dr · dr de  =  1   r02 · d2U dr2 · r0 E  =  1   r0   · d2U  dr2
		Aha! Der E-Modul "steckt" komplett in der 2. Ableitung des Bindungspotentials!
	Falls unser Bindungspotential um das Minimum herum halbwegs "harmonisch" ist, d.h. der Parabel einer idealen Feder entspricht, ist die 2. Ableitung eine Konstante – eben die "Materialkonstante " Elastizitätsmodul.
		Das können wir leicht prüfen: Falls E = ds / de = const wirklich gilt, messen wir im Zugversuch als Verformungsdiagramm s(e) eine exakte Gerade. Aus evtl. Abweichungen von einer exakten Geraden können wir auf Abweichungen des Bindungspotentials von einer Parabel schließen.

	Wir werden radikal
	Für das Bindungspotential eines beliebigen Materials haben wir uns schon eine relativ allgemeine Näherungsformel erarbeitet; sie lautete
		UBindg  =    –  A r n  +   B r m Bindungspotential mit ausgeprägtem Potentialtopf.
		Wir haben 4 Unbekannte in dieser Gleichung: A, B, m , n, über die wir nicht allzuviel wissen. Was wir jedoch wissen - weil es einfach zu messen ist - sind die Zahlenwerte für den Gleichgewichtsabstand r0 und für die Bindungsenergie U0.
		Wir machen also folgendes: Wir substituieren A und B durch r0 und U 0, differenzieren die erhaltene Gleichung 2 mal, teilen das Ergebnis durch r0 und erhalten den E-Modul als Funktion von U0, r0, m und n.
		Viel Glück!
	Schon wieder stoßen wir auf ein typisches Problem der MaWi: Die Mathematik wird schnell mal (etwas) anspruchsvoll; das Ergebnis ist aber einfach. Es lautet:
		E  =   1  · d2U    =  n · m · U0  r 0 dr2  r03
	Warum ist die Mathematik anspruchsvoll? Weil wir für die Substitution Gleichungen n-ten (oder m-ten) Grades zu lösen haben, und dafür gibt es für n > 4 kein "Rezept" (= Lösungsformel) mehr!
		Wer mal schauen will, wie gut sie in Mathe ist, kann's gern mal probieren. Hier ist der Link zu dieser Extra Aufgabe für Spezialistinnen.
	Der Rest glaubt's einfach (oder schaut die Lösung zur obigen Aufgabe an) und überlegt sich, ob man mit der obigen Formel noch was machen kann.
		Man kann. Zunächst mal nehmen wir wahr, dass r 03 in etwa dem Atomvolumen entspricht, das wir sehr leicht über die Dichte des Festkörpers erhalten können. Die Bindungsenergie U0 muss etwas mit dem Schmelzpunkt Tm zu tun haben, denn am Schmelzpunkt gehen per Definitionem die Bindungen auf. Im Großen und Ganzen muss die thermische Energie kBT m, d.h. Boltzmannkonstante kB mal Schmelzpunkttemperatur ungefähr gleich U0 sein.
	Aufgepasst! Wir haben gerade so nebenbei eine erste sehr wichtige Eigenschaft aus dem Bindungspotential "abgeleitet". Den Schmelzpunkt eines Materials!
		Aber es gibt eine Einschränkung: Die Gleichsetzung U0 = kBTm ist gut genug für qualitative oder Größenordungsbetrachtungen, aber nicht gut genug für die Berechnung genauer Zahlenwerte für Tm .
	Für den E-Modul bekommen wir jedenfalls als Faustformel:
		E  »   const. · kB Tm r0 3    »   80 kBTm r03
		Der Faktor 80 für n · m und die sonstigen Näherungen ist an experimentelle Werte angepaßt.
		Das ist nun wirklich eine simple Formel, die aber gar nicht so schlecht ist. Sie stimmt ganz gut für alle Bindungstypen und fast alle Materialien, wie in einem speziellen Illustrationsmodul gezeigt.
		Aber es gibt eine große Ausnahme; vergleiche einen weiteren Illustrationsmodul aus dem MaWi-I-Hyperskript! Man kommt mit der Faustformel nicht unter E » 1 GPa. Was stimmt also beim Gummi (EGum << 1 GPa) nicht? Wir kommen darauf zurück!
	Um sicher zu sein, dass alles sitzt, machen wir noch die folgenden einfachen Übungen:
		Übungsaufgabe Aufgabe 2.1-2
		Fragebogen Einfache Fragen zu 2.1.2
		Fragebogen "Multiple Choice"-Fragen zu 2.1.2

© H. Föll (MaWi für ET&IT - Script)