 |
Wir steigen eine Höhe h die Treppe hoch und haben die potentielle Energie
U =
m · g · h gewonnen (g = Erdbeschleuningung, m = Masse). |
|
 |
Genauer gesagt war es mechanische potentielle Energie; außererdem haben
wir ohne nachzudenken den Nullpunkt
der Höhenskala auf die Ausgangshöhe gelegt. Wir befinden uns jetzt auf dem Potentialniveau oder kurz auf
dem Potential
U(h);
man sagt auch, wir "haben" dieses Potential. |
|
 |
Der Zuwachs an Potential oder potentieller Energie kommt von einer Arbeitsleistung
= Kraft (F) mal Weg (r), oder genauer gesagt Integral Fdr (wobei hier die
Kraft gemeint ist, die wir auf den Probekörper ausüben, um ihn zu bewegen). Nur wenn der Wert des Integrals
vom Anfang zum Endpunkt vom Weg unabhängig ist, können wir von einem Potential reden. Für U = m · g · h
gilt das – die potentielle Energie, die wir nach Bewältigung des Höhenunterschieds h gewonnen
haben, hängt nicht davon ab, ob die Treppe steil oder flach ist, Kurven hat oder gerade ist. |
|
 |
Unterliegt der Probekörper einem gegebenen Kraftfeld F(r),
ergibt sich die potentielle Energie als Integral über –Fdr. Warum das Minuszeichen? Weil
die potentielle Energie zunimmt, wenn der betrachtete Probekörper entgegen der auf ihn vom Kraftfeld
ausgeübten Kraft verschoben wird! Damit ergibt sich für eine Verschiebung in einem radialsymmetrischen Zentralkraftfeld
(wo also der Betrag der Kraft nur vom Abstand zum Koordinatenursprung abhängt und die Kraft zum/vom Koordinatenursprung
radial hin/weg gerichtet ist), die bei r0 beginnt und bei rh endet (wobei
rh = r0 + h), die zugehörige potentielle Energie aus dem Integral |
| |
| U(h) = – | rh
ó
õ
r0 |
F(r) · dr. |
|
|
| |
|
|
 |
Dieser Link
erklärt das präzise und mathematisch (und dreidimensional). Man kann sich das anschauen, muß aber nicht.
|
|
 |
Jeder und jedem ist hoffentlich klar, daß die Formel U = m · g · h
sich nicht
direkt aus obigem Integral ergibt (die Gravitationskraft ist ja proportional zu (m 1·m2)/r2),
sondern nur eine Näherung für kleine h darstellt. Wem das nicht klar ist, der sollte unbedingt die
erste Aufgabe der einfachen Fragen machen. |
 |
Wenn wir ein bißchen verallgemeinern, haben wir gegen die von der Gravitation
stammenden Bindungskräfte
zwischen der Erde und einem Menschen, uns ein bißchen weiter vom Bindungspartner "Erde" entfernt. Der
"Bindungsabstand" hat sich vergrößert. |
|
 |
Die von der Gravitation herrührende Bindungskraft möchte uns eigentlich zum Erdmittelpunkt
ziehen. Wir kämen erst zur Ruhe wenn die Schwerpunkte der beiden Körper den Abstand Null haben. Das klappt aber
nicht, denn sobald wir auf dem "Boden" stehen verhindert eine sehr starke abstoßende
Kraft, die bei einem bestimmten Abstand r0 zwischen Erdmittelpunkt und Massenschwerpunkt exakt
gleich groß ist wie die anziehende Gravitationskraft, daß wir weiter Richtung Erdmittelpunkt fallen |
|
 |
Zwischen den beiden Körpern Erde–Studierender stellt sich der Gleichgewichtsabstand
r0 = rErde + rStudi »
rErde ein; die Summe aus den "Radien" der beiden Partner. |
|
 |
Wollen wir den Abstand um ein –
Dr
verringern, müssen wir, wie unten gezeigt, erheblich mehr Arbeit investieren im
Vergleich zu einem + D
r = h im obigen Beispiel. |
|
|
 |
| Aus "Asterix und die Normannen",
Copyright Dargaud S.A. und EHAPA Verlag |
|
 |
Wir betrachten jetzt ein NaCl-Molekül; die Bindungspartner sind jetzt
die Atome oder besser Ionen. Das Na-Atom
hat sein überschüssiges Elektron dem Cl-Atom übergeben, das
gerne eins mehr hätte; beide liegen jetzt als Na+- und Cl--Ionen
vor. |
|
 |
Zwischen den Ionen wirkt jetzt nicht nur die (vollständig vernachlässigbare)
Gravitation, sondern die anziehende Coulombkraft als die Bindungskraft, die das Molekül zusammenhält.
|
|
 |
Aber auch hier fallen die Zentren oder Ladungsschwerpunkte
der Ionen nicht aufeinander, sondern arrangieren sich ebenfalls in einem Gleichgewichtsabstand r0 =
r1 + r2; die ri
sind die jeweiligen Ionenradien, die jetzt aber ungefähr gleich groß sind. |
| |
|
|
 |
Wollen wir die beiden Ionen auseinanderbringen, d.h. den Abstand r
= ¥ einstellen, müssen wir dazu die Arbeit U¥ leisten; es gilt (mit qi = Ladung des Ions i,
e = Elementarladung = 1,602 · 10–19 C, e0
= dielektrische Suszeptibilität des Vakuums = 8,854 · 10–12 As/Vm): |
| |
| U¥ = |
¥
ó
õ
r0 |
|q1 · q2|
4p · e
0 · r 2 | · dr | = |
e2
4 p · e0 · r0 |
|
|
|
 |
Wir haben damit die gesamte Arbeit ausgerechnet, die man braucht, um die beiden
Ionen gegen die Coulombkraft vollständig zu trennen. |
 |
Wer auch nur das geringste Problem mit dieser Gleichung
hat, tut gut daran, die Fragen und Übungen zu diesem Modul sehr sorgfältig durchzuarbeiten. Wir konzentrieren
uns in dieser Vorlesung auf das grundsätzliche Verständnis und nicht aufs "Rechnen". |
|
 |
Zur
potentiellen Energie bzw. zum Bindungspotential
kommen wir, wenn wir das Integral für einen beliebigen Abstand r > r0 ausrechnen
(das ist dann die zu leistende Arbeit, um den Abstand von r0 auf r zu erhöhen).
Allerdings ist die Wahl des Nullpunktes der Energieskala frei, und gewönlich wird bei den anziehenden Coulombkräften
die Null ins Unendliche gelegt. Im Gleichgewichtsabstand r0 beträgt damit die potentielle
Energie –U¥
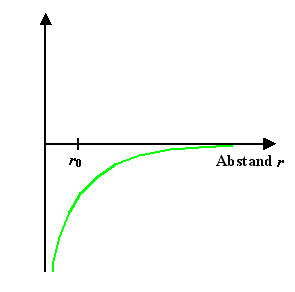
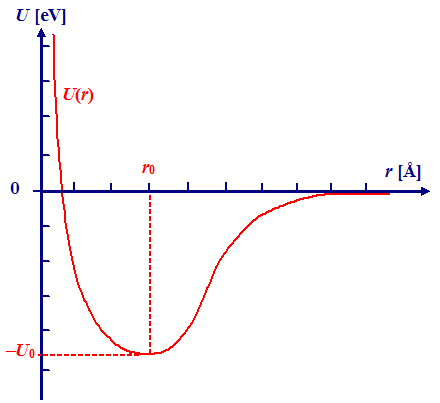
. Zeichnen wir einen schematischen Graphen, sieht das so aus wie im Bild unten links gezeigt. |
| |
 |
 |
 |
| Anziehendes Coulombpotential |
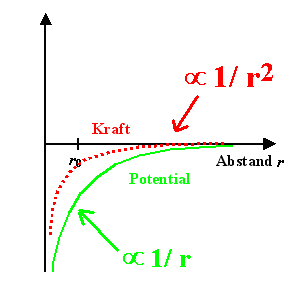
Anziehendes Coulombpotential
und zugehörige Kraft |
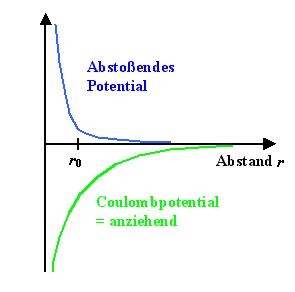
Anziehendes Coulombpotential
und abstoßendes
Potential |
|
 |
Jetzt betrachten wir mal das inverse
Problem: Der Potentialverlauf zwischen zwei wechselwirkenden Körpern sei von Gott oder seinem Stellvertreter auf Erden
(für Studis ist das der Professor oder die Professorin) gegeben, wie in der Kurve im obigen Bild links. Wir interessieren
uns jetzt für die zugehörige Kraft
F zwischen den Körpern. |
|
 |
Wie das geht, sollte klar sein; wir haben |
| |
| eindimensional: | dreidimensional
(Unterstrich = Vektorsymbol): |
| F = – | dU( r)
d r |
| F = – |
grad[U(r)] |
= – 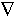 U(r) U(r) |
in Komponenten also
| Fx = – | ¶U
¶ x | , |
Fy = – | ¶U
¶ y | , |
Fz = – | ¶U
¶ z |
|
|
|
 |
Im rechten und unteren Teil der Gleichung sind wir dreidimensional geworden, dazu haben wir F und r als
Vektoren
geschrieben (das geht in simplem HTML nur mit Unterstrich). |
|
 |
Die geschweift geschriebenen Buchstaben "¶"
bezeichnen partielle Ableitungen, sind aber ganz analog zu den gewohnten Ableitungen zu verstehen, die mit "d"
notiert werden. Partielle Ableitungen werden bei Funktionen mehrerer Variabler benötigt, weil man solche Funktionen
nach jeder Variable einzeln ableiten kann. Bei der Berechnung einer partiellen Ableitung sind alle übrigen Variablen
(alle außer der, nach der abgeleitet werden soll) als Parameter mit festen Werten zu behandeln. Alles, was
man über gewöhnliche Ableitungen gelernt hat, gilt somit auch für partielle Ableitungen – bloß
gibt es "die Ableitung" einer Funktion mehrerer Variabler nicht (logisch!). |
|
 |
Weil die partiellen Ableitungen bei Ortskoordinaten häufig im "Dreierpack"
auftreten (wie z. B. oben für die drei Komponenten der Kraft F als partielle Ableitungen des Potentials
hingeschrieben), wird so ein Dreierpack in Vektorform häufig mit dem Symbol  (genannt "Nabla-Operator")
abgekürzt. (genannt "Nabla-Operator")
abgekürzt. |
|
 |
Sehr salopp und sehr pragmatisch formuliert, ist der Nabla-Operator einfach der
(Spalten-)Vektor der partiellen Ableitungsoperatoren nach den drei Ortskoordinaten. Mathematisch gesehen, ist diese
Aussage Unfug, denn als Operator kann er kein normaler Vektor sein (logisch; vielmehr ist er ein Element des sog. Tangentialraumes
– aber halt, das ist Differentialgeometrie und damit hier nicht dran). Sie trifft aber den Kern, wenn es um den rechentechnischen
Alltag geht: Wenn man Nabla auf eine skalare Funktion der drei Variablen x, y und z losgelassen hat,
kommt ein normaler Vektor dabei heraus. Dieser Vektor ist dann der Gradient der betreffenden skalaren Funktion.
|
|
 |
Ausblick: Man kann den Nabla-Operator auch auf eine vektorielle Funktion
der drei Variablen x, y und z loslassen (= Vektorfeld), und zwar im Skalarprodukt (dann erhält
man die Divergenz des Vektorfeldes) oder im Kreuzprodukt (dann erhält man die Rotation des Vektorfeldes);
aber das benötigen wir erst später. Außerdem kann man das Skalarprodukt zwischen zwei Nabla-Operatoren bilden,
auf diese Weise erhält man den (skalaren) Operator der Summe der zweiten partiellen Ableitungen nach den drei Ortskoordinaten,
auch als Laplace-Operator bekannt; das wird uns in Kürze begegnen. (Der Laplace-Operator liefert sozusagen die
Divergenz des Gradienten einer Funktion.) |
 |
Wenn man also eine Potentialkurve hat wie im Bild oben links gegeben, kann man
durch (graphisches) Differenzieren sofort eine Kraftkurve (schematisch) einzeichnen; das ist im mittleren
Bild gezeigt. |
 |
Wir betrachten jetzt den Fall, daß die beiden Ionen sich wieder liebhaben
und möglichst dicht aufeinander hängen wollen. |
|
 |
Das geht aber nicht so einfach. Kommen sie sich zu nahe, beginnt eine sehr stark
abstoßende Kraft zu wirken, die mit betragsmäßig größer werdendem Dr
zu kleineren Abständen hin erfahrungsgemäß sehr schnell (= mit hoher
Potenz von Dr) gößer wird. Man kann zwei Körper = 2 Atome
nicht ineinanderschieben! |
|
 |
Diese abstoßende Kraft ist übrigens dieselbe, die die Gravitation
daran hindert, uns zum Erdmittelpunkt zu ziehen. |
 |
Wie lautet die Formel für die abstoßende Kraft, mit
der wir dann das Abstoßungspotential berechnen können? Die Antwort auf diese Frage ist symptomatisch für die Materialwissenschaft:
|
| |
Es gibt oft keine einfachen Formeln für einfache Tatbestände.
Aber:
Es gibt manchmal sehr einfache Formeln oder Graphiken für sehr komplexe Situationen. |
|
|
|
 |
Zur Berechnung der abstoßenden Kraft zwischen Atomen bzw. Ionen braucht
man die Quantentheorie. Es gibt dann i.d.R. keine einfachen Formeln mehr, oft gibt es
überhaupt keine "hinschreibbaren" (= analytischen) Formeln mehr. Das heißt aber nicht,
daß die zugrundeliegenden Phänomene an sich schwierig sind! |
 |
Wir behelfen uns hier schlicht damit, daß wir das abstoßende Potential
so hinzeichnen, wie es ungefähr aussehen muß. Das ist im rechten
Teil des obigen Bildes getan. |
|
 |
Die Kraftkurve dazu denken wir uns (bzw. machen das in der Übung); damit werden auch
die Vorzeichen klar. |
 |
Jetzt kommt der entscheidende Schritt: Potentiale darf man einfach (vorzeichenrichtig)
addieren, da sie vom Weg unabhängig sind. Wir tun das mal (und zwar graphisch) und bekommen für das gesamte Bindungspotential
von Na+-Cl– (und qualitativ auch für jedes andere Ionenpaar) die unten gezeigte
Kurve. |
| |
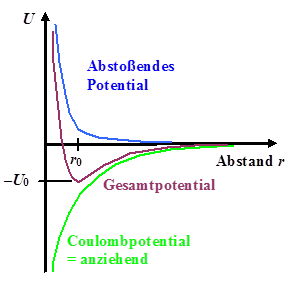 |
| Bindungspotentialkurve für Ionen |
|
 |
Wir haben eine Potentialkurve mit einem Minimum
der betragsmäßigen Tiefe U0
bei r0. In einem solchen Fall reden wir immer von einem Potentialtopf! |
|
 |
Im Gleichgewichtsabstand r0 ist das Potential negativ: U(r0)
= –U0. Wie bereits oben besprochen, ist folglich die Arbeit U0 aufzubringen,
um die Ionen voneinander zu trennen (Abstand auf "unendlich" erhöhen). |
|
 |
Wir können daher U 0, den betragsmäßigen Wert des
Bindungspotentials im Minimum, mit Fug und Recht auch die Bindungsenergie der Ionen nennen. (Nochmal: U(r0) ist negativ; Bindungsenergien
gibt man aber als positive Zahl an.) |
|
 |
U0 ist allerdings noch nicht die Bindungsenergie des NaCl-Moleküls. Warum? Darüber sollte man erst mal selbst
nachdenken. |
|
|
|
Bindungspotentiale verallgemeinert
|
| |
|
 |
Wir machen jetzt eine leicht zu verstehende Verallgemeinerung mit weitreichenden
Folgen. |
 |
1. Wir nehmen viele
Ionen in einer Fläche und nicht nur zwei wie oben. Falls NaCl eine atomare Schicht bilden würde, sähe
das z.B. (halbwegs maßstabsgetreu) wie folgt aus: |
|
|
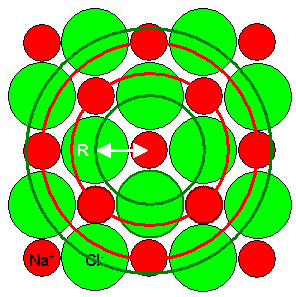 |
| Maßstabsrichtige NaCl-Schicht |
|
|
 |
Wenn wir jetzt für das zentrale Na+-Ion die Arbeit ausrechnen,
um es (nach "oben") zu entfernen, addieren wir "einfach" alle Coulombkräfte auf, und zwar als Funktion
des jeweiligen Abstandes (durch die Kreise markiert). |
|
 |
Wir haben eine Folge von anziehenden und abstoßenden Kräften. Falls
wir den zweidimensionalen Kristall gleich ins Unendliche ausdehnen (schwierig zu zeichnen), bekommen wir eine unendliche
Reihe, die aufzusummieren wäre. Das ist mathematisch sehr anspruchsvoll, aber es geht. |
 |
Wir erhalten ein Potential, das graphisch genauso aussieht wie das im entsprechenden
Bild für zwei Ionen gezeigte. Nur die Zahlen an den Achsen würden sich etwas
ändern. Da wir schlauerweise keine eingezeichnet haben, ändert sich erst mal gar nichts. |
 |
2. Wir gehen einen Schritt weiter: Wir nehmen viele Ionen,
aber jetzt sogar dreidimensional angeordnet – halt den realen NaCl-Kristall. |
|
 |
Es ist jetzt nicht so klar, wie wir ein Ion entfernen. Darüber brauchen wir uns aber
keine Sorgen zu machen, denn das zugehörige Potential ist vom Weg unabhängig. |
|
 |
Die Berechnung wäre ähnlich wie oben, nur wird die unendliche Folge von abstoßenden
und anziehenden Kräften, über die zu integrieren ist, noch komplizierter; mehr dazu im Link
. |
|
 |
Wir brauchen das aber gar nicht selber zu tun – Herr Madelung
(und viele nach ihm) haben es schon für uns getan. Das Ergebnis ist trotz sehr trickreicher Mathematik verblüffend
einfach: |
| |
Coulombpotential für ein
Ion des Na+-Cl–-Moleküls | |
U(r) = |
– |
A'
|r | |
| |
| |
| |
Coulombpotential für ein
Ion des Na+-Cl--Kristalls |
|
U(r) = |
– a M
| A'
|r| |
|
|
 |
Die Konstante A' ist uns von der Übung
her bekannt (??), der Faktor a
M heißt Madelungkonstante. |
|
 |
Der exakte Wert der Madelungkonstanten hängt natürlich von den Ionensorten und den
damit verknüpften Bindungslängen sowie der dreidimensionalen Anordnung ab. Für Na+ -Cl–
haben wir zum Beispiel aM = 1,748. Im allgemeinen Fall liegt die Madelungkonstante
zwischen ca. 1,5 und 4,5; genaue Werte gibt's im Link.
|
|
 |
Das bedeutet erst mal, daß ein Ion im Kristall aM-mal
fester gebunden ist als im Molekül. |
 |
3. Wir gehen noch einen Schritt weiter: Was uns für das anziehende
Potential recht war, gilt auch für das abstoßende Potential. Versuchen wir, ein Ion in einem NaCl-Kristall
dichter auf einen Nachbarn zu drücken, wird die abstoßene Kraft mit abnehmendem Abstand sehr schnell anwachsen;
das zugehörige "abstoßende" Potential Uab sieht schematisch aber nicht anders
aus als oben gezeigt. |
|
 |
Um eine halbwegs passende Formel zu haben, beschreiben wir es als Uab
»
B/rm. Wir haben damit zwei weitere Konstanten B und m eingeführt,
über die wir noch nichts wissen, außer daß m >> 1 sein sollte. |
|
 |
Damit haben wir für das Bindungspotential von Na+ -Cl–
und damit auch für alle anderen Ionenbindungen die (ungefähre) Formel |
| |
|
|
 |
In dieser Allgemeinheit gilt das außerdem nicht nur für Na+Cl–
, sondern für alle Ionen in allen
Ionenkristallen. |
 |
Bevor wir weiter verallgemeinern, bleibt noch schnell die Frage zu klären,
warum wir betont haben, daß wir über das Bindungspotential von Na+-Cl– reden
und nicht über das von Kochsalz, NaCl. |
|
 |
Einfach: Bevor wir Na+ und Cl–
haben, müssen wir erst mal Na und Cl ionisieren
. Das geht nicht ganz ohne Energieaufwand. Zwar hat das Na-Atom ein Elektron "zuviel", und ein Cl-Atom
hat ein Elektron "zu wenig", aber einfach so wird weder das Na-Atom sein überschüssiges Elektron
hergeben noch das Cl-Atom eines anlagern. Die enge Bindung zwischen Atomen X und Y beginnt sozusagen
mit einem Flirt, in dem erst mal eine kleine Aufmerksamkeit (ein Elektron) überreicht wird. Nur wenn der prospektive
Partner das Geschenk annimmt (= bindet), geht's weiter. |
|
 |
Wir beschreiben die Ionisierung deshalb durch die einfachen Beziehungen: |
| |
| Na | + | 5,14 eV |
Û | Na+ |
+ | e– |
| Cl | – | 3,61 eV |
Û |
Cl – | – |
e– | | |
| | | |
| |
| Besser formuliert: | | Cl – |
+ | 3,61 eV |
Û | Cl |
+ | e– |
| | | | |
| | |
| Gesamtbilanz |
| Na + Cl + 1,43 eV |
Û | Na+ |
+ | Cl – |
|
|
 |
Damit haben wir auch schon zwei Kennzahlen von Atomen kennengelernt: |
 |
1. Die Ionisierungsenergie
I = Energie, die es braucht, um bei einem Atom X ein Elektron abzutrennen: XAtom
+ I = X+Ion + e– |
|
 |
Nebenbei haben wir noch unsere Hauptmaßeinheit für Energien definiert: das Elektronenvolt
(Symbol: eV). Dazu machen wir eine extrem einfache schnelle Übung: |
| |
|
 |
2. Die Elektronenaffinität
A, definiert nach X–Ion + A = XAtom + e–.
Man kann das als Energie sehen, die frei wird, wenn ein neutrales Atom ein Elektron bindet, oder als die "Ionisierungsenergie"
(die Abtrennenergie) für das negativ geladene Ion. |
|
 |
Hier treffen wir auch zum ersten Mal auf den  1. Hauptsatz der Materialwissenschaft 1. Hauptsatz der Materialwissenschaft  : : |
| |
| Mit Gewalt kann man alles kaputtmachen |
|
|
 |
Man kann mit Gewalt – d.h. mit hinreichend viel Energie, die zur Ionisierung eingesetzt
wird – jedem Atom ein Elektron wegnehmen. Man kann aber Atome, die kein zusätzliches
Elektron haben möchten, nicht zwingen, eines zu binden. |
|
 |
In anderen Worten: Die Ionisierungsenergie ist immer eine
positive Zahl; die Elektronenaffinität kann in Prinzip aber auch negativ werden. Das würde bedeuten, daß
man Energie gewinnt (und nicht hineinstecken muß), um einem negativ geladenen Ion sein Elektron wegzunehmen, oder
schlicht, daß das Elektron sofort "von allein abfällt". Da es dann keine negativ geladenen Ionen geben
kann, ist die Angabe einer Elektronenaffinität in diesen Fällen (z. B. für alle Alkali- und Erdalkali-Elemente
[warum???]) sinnlos. Mehr dazu in diesem Link. |
 |
Von dem Bindungspotential U0 der Ionen,
wie oben angegeben, müssen wir also noch die Bilanz der Energien abziehen, die man
zunächst braucht, um aus den Atomen Ionen zu machen. |
|
 |
Das verschiebt aber nur den Nullpunkt der entsprechenden Potentialkurven – den wir schlauerweise
nirgendwo eingezeichnet haben. Auch die Formel können wir beibehalten, solange wir keine Zahlenwerte angeben. |
|
 |
Damit haben wir "eigentlich" die Bindung reiner Ionenkristalle schon abgehandelt.
Wir werden uns das aber noch ein bißchen näher ansehen. Vorher machen wir allerdings erst noch den nächsten
Schritt in Richtung Verallgemeinerung: |
 |
4. Was für die Anziehung, also die Bindungskräfte, zwischen zwei
Ionen gilt, läßt sich jetzt auf jeden Typ von Bindung verallgemeinern. |
|
 |
Was immer die Anziehung bewirkt und zur Bindung führt – z. B. für die Cl-Atome
im Cl2-Gas –, hat ein Potential Uan, das mit kleiner werdendem Abstand
"runter"geht, also schematisch immer noch wie im Bild oben links aussieht. Solche
Kurven kann man in Näherung immer durch einen Ausdruck in der Form Uan
= –A/rn beschreiben, mit n = 1 für Ionen und n irgendeine
Zahl > 1 für andere Bindungen. Die Madelungkonstante steckt im Zweifel in der Konstanten A
(jetzt ohne Strich). |
|
 |
Damit haben wir ein ganz allgemeines
Bindungspotential UBindg definiert: |
| |
| UBindg = | – |
A
r n | + |
B
r m | | |
| | |
| | |
anziehend | | abstoßend |
|
 |
|
 |
Cui bono – wem nützt's? Nun, wie wir sehen werden, haben wir mit dem
allgemeinen Bindungspotential eine Menge erreicht:
- Wir haben einige wesentliche Eigenschaften der Kristalle (wenn nicht gar aller fester
Stoffe), die wir im weiteren Verlauf kennenlernen werden, damit im Grunde schon "erschlagen".
- Wir haben einen guten Grund, uns jetzt schon nach der Rolle der Temperatur T zu fragen (die bisher gar
nicht vorkam), und dabei einige erste Antworten zu finden.
- Wir haben den Schlüssel zur Struktur der Festkörper (Kristall, welcher Kristalltyp?, ...).
- Wir haben einen generellen Ansatz zur Behandlung materialwissenschaftlicher Fragen gefunden, der ausbaufähig sein
wird.
- Wir haben gleich zu Beginn verstanden, daß es um's Prinzip geht, und daß trotz komplizierter Mathematik
einfache Ergebnisse herauskommen können.
|
 |
Diese Punkte werden wir im folgenden aufgreifen und vertiefen. |
| |
|
| |
|
© H. Föll (MaWi für ET&IT - Script)