|
Hier sind einige schnelle Fragen zu 2.1.1: Das Bindungspotential |
|  |
Erkläre die Gleichung unten und berechne dazu insbesondere das Integral für einen
beliebigen Abstand r' – und damit das Potential
U(r) für die Coulombkraft. |
| |
| W (r) = |
¥
ó
õ
r0 |
q1 · q2
4p · e0 · r
2 | · dr | = – |
e2
4p · e0 · r0 |
|
|
|
 |
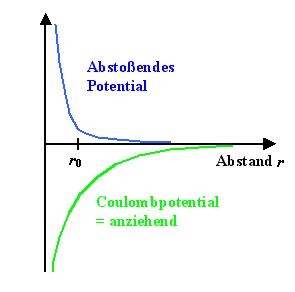
Vergleiche das Coulombpotential zunächst qualitativ
(d. h. nur bezüglich der mathematischen Funktionalität) mit dem Potential der Gravititationskraft; dann quantitativ. Um wieviel größer ist die Coulombindungsenergie zwischen zwei typischen
Ionen mit Masse mion im Abstand r im Vergleich zur Gravitationsbindungsenergie? |
|
 |
Wieso ist das mit der Coulombkraft verknüpfte Potential "komplizierter" als
die potentielle Energie
mgh, die man nach gemeinhin beim Herumturnen auf der Erdoberfläche hat? |
|  |
Wie ist das mit den Vorzeichen? Vergleiche für Gravitation und Coulombkraft. |
|
 |
Warum muss das abstoßende Potential ungefähr
so aussehen wie gezeichnet (Bild unten links)? Wie sieht die zugehörige Kraftkurve aus? |
| |
 |
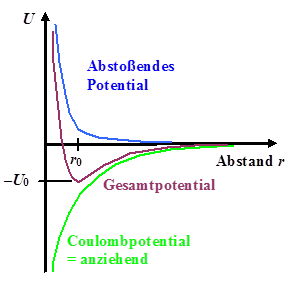 |
| Coulombpotential und abstossendes Potential |
Gesamtpotential (Summe Einzelpotentiale) und
Bestimmungsgrößen |
|
|
 |
Warum ist U0
nicht die Bindungsenergie des NaCl-Moleküls, sondern die Bindungsenergie der Ionen
Na+ und Cl–? Was muss noch dazu kommen, damit es die Bindungsenergie des NaCl-Moleküls wird? |
 |
Zeichne für dasModellpotential im Link folgende Größen so quantitativ als möglich ein: |
|  |
Die wirkende Kraft: Auf
Vorzeichen aufpassen und Maxima / Minima sowie Wendepunkte, wo immer erforderlich, berücksichtigen. Man darf annehmen,
dass die Potentialkurve ums Minimum herum ganz gut durch eine Parabel dargestellt werden kann. |
|  |
Nur mal so zeichnen wir noch die 2. Ableitung der Potentialkurve ein.
Was könnte der Nulldurchgang für eine Bedeutung haben?
Hinweis: Man stelle sich vor, man versuche "per Hand" ein Molekül zu
zerreißen, und betrachte die Kraft, die dazu nötig ist. |
 |
Was ist: |
|
 |
Die Madelungkonstante? Wie kann man sie im
Prinzip ausrechnen? |
|
 |
Die Ionisierungsenergie
? Was kann man über Zahlenwerte qualitativ sagen (z. B. bei Betrachtung von Alkali-Metallen, Halogenen, Edelgasen,
Edelmetallen, ...) |
|
 |
Die Elektronenaffinität? Woduch unterscheidet
sie sich prinzipiell von der Ionisierungsenergie?
Hinweis: Übers Vorzeichen nachdenken. |
|
| |
 |
Hier sind einige schnelle Fragen zu 2.1.2: Bindungspotentiale, Federn und
Elastizitätsmodul |
|
 |
Was für eine Potential muss eine ideale Feder (mit einer Federkonstante)
haben, d. h. was für ein Funktionstyp liegt vor? |
|
 |
Wie ist Dehnung definiert; was ist die Maßeinheit? |
|
 |
Was unterscheidet mech. Spannung vom Druck? Wie vergleichen sich die Maßeinheiten? |
|
 |
Was verbindet Federkonstante kFed und
E-Modul?
Hinweis 1: Man betrachte keine gewickelte Feder (dann ist die Federkonstante auch von
der Art der Wicklung abhängig), sondern ein gerades Stück (wie im Bild
gezeigt). Zeige, dass gilt:
kFed = F/D
l = E · (A/l) = E ·r0 mit r0
» Bindungsabstand.
Hinweis 2: Man darf Federn und Materialien so klein als möglich machen, aber nicht
kleiner. |
|
 |
Ist s = 1 GPa im täglichen Leben eine
große oder eher normale mech. Spannung? Überschlage z. B. die Spannung in einem Kranseil, das bei einem Querschnitt
von 1 cm2 locker etliche Tonnen trägt. |
|
 |
Skizziere in einem Spannungs-Dehnungs-Diagramm die Verformungskurve für
folgende Fälle (benutze halbwegs realistische Dehnungen und einen Stern o.ä. für Bruch; benutze das Diagramm
im Skript als Ausgangspunkt, es zeigt ein mittelhartes duktiles Material):
- Ein sehr hartes
(großer E-Modul) und sprödes Material.
- Ein deutlich weicheres aber immer noch sprödes
Material.
- Ein typisches Metall
(Hinweis: Metalle sind nicht spröde!)
- Ein Elastomer
, vulgo Gummi.
Hinweis: Man kann die Frage mit etwas Vorstellungskraft und der alltäglichen Erfahrung
beantworten, man muss das nicht "gelernt" haben. |
|
 |
Wie kann man den E-Modul bei (quantitativ) gegebenem Potentialtopf
graphisch bestimmen? |
|
 |
Was verbindet den Schmelzpunkt und das Bindungspotential? |
|  |
Warum ist der E-Modul in etwa proportional zum Schmelzpunkt? |
| | |
|
 |
Hier sind einige schnelle Fragen zu 2.1.3: Bindungspotentiale und weitere Eigenschaften |
| |
| |
|
 |
Was ist an dem typischen Bild eines Kristalls, wie nebenstehend gezeigt, im Grunde falsch? |
 |
Was ist Temperatur ganz allgemein? Konkret für einen Kristall? Wie müsste man das in
die Skizze einzeichnen (und warum tut man das i.a. nicht)? |
|
|
 |
Hat ein Auto, das mit v = 100 km/h und bei 20 o C durch die Gegend fährt,
eine größere thermische Energie als wenn es geparkt ist? Hat es eine größere
Gesamtenergie als wenn es geparkt ist? Wo kommt ggf. der Unterschied her? |
| | |
| |
|
 |
Zeichne einen tpyischen Bindungspotentialtopf. Zeichne schematisch ein, wo das
gebundene Atom sich bei 0 K und bei zwei endlichen Temperaturen befindet (eine davon dicht am Schmelzpunkt). Wo ist
es im Mittel? Was kann man zur mittleren Energie aussagen? |
|
 |
Wie ist der thermische Ausdehnungskoeffizient definiert, und wie ergibt er sich
(graphisch) aus dem Potential? |
|
 |
Wie groß ist die Eigenfrequenz einer Masse m an einer Feder
mit Federkonstanten kFed? |
|
 |
Mit welcher Frequenz (Größenordnung) vibrieren Atome im Kristall? Was
bestimmt die (mittlere) Amplitude? Wo liegt diese Frequenz relativ zu bekannten Bändern im elektromagnetischen Spektrum? |
|
 |
Wie ergibt sich (graphisch) die maximale Bruchspannung und -dehnung aus dem Potential?
Welche Größenordung hat die max. Bruchdehnung in %? Was sagt das Experiment? |
| |
|
© H. Föll (MaWi für ET&IT - Script)