2.1.5 Merkpunkte zu Kapitel 2.1 "Bindungspotentiale und erste Eigenschaften"

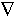	Zwischen zwei Ionen gibt es anziehende und abstoßende Kräfte; im Gleichgewichtsabstand r0 = Bindungsabstand ist die Summe der Kräfte = 0			U(r) = – r ó õ r0 F(r ') · dr' F = – grad[ U( r)]  =   – U(r) Fx = – ¶ U ¶ x ,   Fy = – ¶U ¶y ,    Fz = – ¶U ¶z
		Für Ionen ist die anziehende Kraft=Coulombkraft; sie nimmt als Funktion des Abstands r mit r–2 ab.
		Über die abstoßende Kraft wissen wir nur, dass sie bei zu großer Nähe sehr schnell sehr groß wird, d. h. mit einer Funktion wie r–m, m >> 2) anwächst.
	Statt Kräften betrachten wir aber besser das zugehörige Potential U(r), gleich dreidimensional als Funktion des Ortsvektors r
		Das Potential der Coulombkraft hat also die Funktionalität UCoulomb µ r–1
	Aus abstoßendem Potential und anziehendem Potential kann man, falls überhaupt eine Bindung vorliegt, durch (vorzeichenrichtige) Addition immer einen Potentialtopf U(r) konstruieren			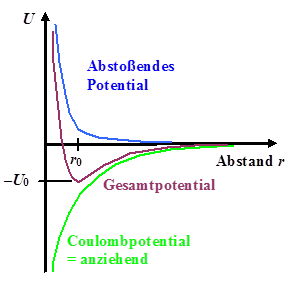Konstruktion Potentialtopf
		Das abstoßende Potential wird mit B / rm beschrieben
		Das anziehende Coulombpotential wird mit –A Cou / r beschrieben; mit A Cou = (q 1 · q2)/4pe0
		Falls wir nicht nur die Coulomb Wechslwirkung zwischen zwei isolierten Ionen betrachten, sondern die zwischen einem Ion in einem Kristall und allen (¥ vielen) anderen, muss ACou mit der Madelung-Konstanten a » 1,5 ... 4,5 multipliziert werden
		Als eine allgemeine Näherungsformel mit A = a · ACou dient dann die Gleichung
		UIon(r) =  B  rm   –   A  r
	Um die Bindungsenergie zu erhalten, muss zur Tiefe des Potentialtopfes U0 noch die Energiebilanz aus Ionisierungsenergie I und Elektronenaffinität A addiert werden, da wir ja zuerst aus Atomen Ionen machen müssen.			XAtom + I  =  X+ Ion + e– X– Ion + A  =  XAtom + e–
		Kleine Ionisierungsenergien liegen im Bereich von 5 eV (Alkali-Metalle), große Elektronenaffinitäten im Bereich 3 eV (Halogene).
	Von der Ionenbindung kommt man leicht zu jeder Bindung: sie braucht einen Potentialtopf und kann immer in folgender Form geschrieben werden:			Im Bindungspotential steckt: Struktur des Festkörpers (Kristall, welcher Typ, ...). Elastizitätsmodul E. Thermischer Ausdehnungskoeffizient a . Schwingungsfrequenz der Atome im Kristall. Maximale Bruchfestigkeit. Ungefährer Schmelzpunkt.
		UBdg(r ) =  B  rm   –   A  rn
		Von den vier Unbekannten A, B, m, n können zwei durch die leicht zu messenden Größen U0 und r0 substitioniert werden; n ist manchmal bekannt (s. o.).
		Im Bindungspotential stecken viele wichtige Eigenschaften des zugehörigen Kristalls.
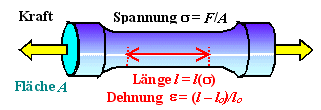
	Der Elastizitätsmodul E misst die durch eine mechanische Spannung s verursachte Dehnung e eines Materials.
		Er ist gegeben durch
		E  =  1   r0  · d2U  dr2

	Die mit der (absoluten) Temperatur T verbundene thermische Energie Etherm folgt der extrem wichtigen Formel des Gleichverteilungssatzes Þ			Bei der (absoluten) Temperatur T hat ein Teilchen in einem Teilchensystem (Kristall, Gas, ...) im Mittel die thermische Energie (innere Energie) UTeilchen= ½f kBT (bei f Freiheitsgraden).
		Die Energie kann nur in Schwingungen der Atome um die Gleichgewichtslage stecken:
	In jedem Augenblick hat ein Atom drei linear unabhängige Geschwindigkeitsvektoren (® kin. Energie; nicht eingezeichnet) und drei linear unabhängige Ortsvektoren relativ zur Ruhelage ( ® pot. Energie); das ergibt sechs Freiheitsgrade für die Energie.
		Die Gesamtenergie einer Schwingung ist aber konstant (= Epot(max) oder Ekin (max) ) und kann deshalb als Energieniveau in den Potentialtopf eingezeichnet werden.
	Der thermische Ausdehnungskoeffizient folgt damit aus der Asymmetrie des Potentialtopfes und kann somit berechnet werden.
	Die Schwingungsfrequenz n ergibt sich aus Massen und "Federkonstante" zu n » 1013 Hz.
	Die max.theoretische Bruchfestigkeit ist bei ca. 30 % Dehnung (e » 0,3) erreicht
		In der Praxis brechen Materialien aber früher, da der Bruch durch Defekte bestimmt wird.
	Der Schmelzpunkt Tm ist ungefähr durch die Tiefe UBdg des Potentialtopfes gegeben: kBTm » UBdg
	Die Art der Bindung bestimmt die atomare Struktur des Festkörpers: Ungerichtete Bindung: Dichteste Packungen (bei elektr. Neutralität) Gerichtete Bindung: Zahl und Anordnung entscheidend
		Für uns besonders wichtig: 4 gerichtete Bindungsarme im Tetraederwinkel (= größtmöglicher gleichgroßer Winkel = Schnittwinkel der Raumdiagonalen eines Würfels)
	Aufgaben:
	Fragebogen Einfache Fragen zu 2.1
	Hier noch ein "Multiple Choice"-Test, der etwas über den Stoff hinausgeht – man kann es ja mal probieren!
	Fragebogen "Multiple Choice"-Fragen zu 2.1

© H. Föll (MaWi für ET&IT - Script)