|
Warum gibt es überhaupt chemische Bindungen? |
|
 |
Weil die Gesamtenergie von Atomen, die sich zusammentun, kleiner sein kann als die der ungebundenen
Atome. |
 |
Ja, und? Was haben die Atome davon? |
|
 |
Wichtig: Die obige Aussage über die "kleinere Gesamtenergie" ist mathematisch
gemeint; es geht also um einen weiter im Negativen liegenden, d. h. absolut gesehen größeren Wert. Also gilt: |
| |
Je größer die Bindungsenergie, desto tiefer die Gesamtenergie,
und desto stabiler die
Bindung – weil dann mehr Energie
aufgebracht werden muß, um die Bindung wieder zu lösen. |
|
|
|
 |
Dieser Satz gilt auch in Verallgemeinerung: Jedwede Absenkung der Gesamtenergie führt
zu einem stabileren Zustand des Systems, und daher ist die Möglichkeit zur Energieminimierung eine "treibende
Kraft" für jedwede Art von Veränderungen, d. h. nicht nur für das Eingehen von Bindungen! |
|
 |
Wie wir später noch sehen werden, gibt es neben der Energieminimierung noch eine weitere,
sehr wichtige "treibende Kraft" für Veränderungen – und zwar eine, die sogar dafür sorgen
kann, daß es zu einem Anstieg (!) der Gesamtenergie kommt. (Hier sei erst mal nur so viel verraten, daß diese
weitere "treibende Kraft" mit der Temperatur zusammenhängt – womit schon mal ein Teilaspekt des Anstiegs
der Gesamtenergie erklärt ist.) |
 |
Zurück zum Thema: Für welche Atomkombinationen klappt das mit der Energieabsenkung
durch Eingehen einer Bindung? |
|
 |
In nullter Näherung – und die reicht für uns hier – gilt schlicht: |
| |
| Bindung gibt's, wenn die Elektronenkonfiguration der beteiligten Atome durch das Eingehen einer Bindung
edelgasähnlicher wird. |
|
|
|
 |
Für Halogene (wer nicht weiß, was das ist, tut gut daran, den Link zu betätigen) ist das Ziel besonders leicht zu erreichen, indem sie noch ein
Elektron von irgendwoher bekommen. Für Alkalimetalle (wer nicht weiß, was das ist ...) ist das Ziel besonders
leicht zu erreichen, indem sie ein Elektron loswerden. |
|
 |
Daß Halogene und Alkalimetalle, falls man ihnen eine Chance dazu gibt, ein Elektron
"springen lassen" und sich dann freudig erregt zusammentun werden, ist klar. |
 |
Die Ionenbindung haben wir im Grunde damit erklärt;
wir haben sie schon vorher bereits abgehandelt. Es ist eine rein elektrostatische
Bindung zwischen zwei (oder mehr) Ionen. |
|
 |
Für die Ionenbindung kennen wir auch wir zwei der vier Parameter des allgemeinen
Bindungspotentials (a ist die Madelungkonstante ):
|
| |
| UBindg | = |
– | A
r
n | + | B
r
m | | | | |
| | |
| | = |
– a | |q|2
4p · e 0 · r
| + | B
r
m |
|
|
 |
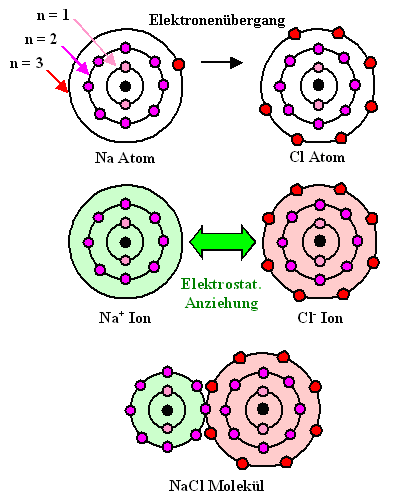
Als Vorbereitung auf das Kommende schauen wir uns die Ionenbindung mal noch in
dieser schematischen Darstellung an: |
|
|
|
|
 |
Die Elektronen des Na- und Cl-Atoms sind schematisch auf ihren
"Schalen" oder "Orbitalen"
eingezeichnet, die mit n = 1, 2, 3, ... durchnumeriert sind. |
|
 |
Die Orbitale wären am liebsten entweder "leer" oder "gefüllt"
mit einer definierten Anzahl von Elektronen; für die beiden gezeigten Atome sollten es 8 Elektronen sein. Daran
gemessen, hat Na erkennbar ein Elektron zu viel, Cl eins zu wenig. Was in so einer Situation passiert, sobald
sich die Atome so nahe kommen, daß sie "handlungsfähig" werden, haben wir bereits
quantitativ beschrieben. |
 |
Was kann man sofort zu den resultierenden Eigenschaften sagen?
|
|
 |
Die reine Ionenbindung wird zwischen Atomen mit kleiner Ionisierungsenergie,
also Alkali- (Li, Na, K, ...) sowie Erdalkalielementen (Be, Mg, Ca, ...), und
Elementen mit großer Elektronenaffinität, also Halogenen
(F, Cl, Br, ...), auftreten. Wer das nicht so direkt parat hat, kann mal hier nachschauen: |
|
 |
Die Bindung ist vollständig ungerichtet.
Wir erwarten dichteste Packung, aber immer so, daß elektrische Neutralität
vorliegt – also LiF (Li+; F–
) oder CaF2 (Ca2+; 2F–, aber niemals LiF
2 oder CaF. Da die Ionen aber verschieden groß sind, ist die optimale räumliche
Struktur nicht unmittelbar klar. In diesem Link (runterscrollen!)
finden sich Bilder und weiterführende Links, falls es jemand genau wissen will. |
|
 |
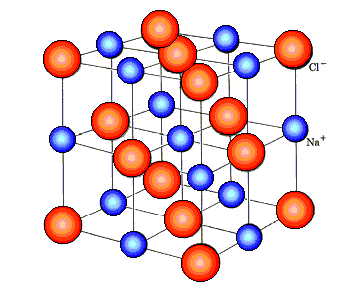
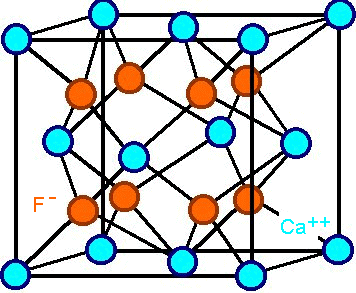
Für die einfacheren Ionenkristalle wie Kochsalz (NaCl) oder Flußspat
(CaF2 ) ist die Kristallstruktur jedenfalls "kubisch", allerdings
auf irgendwie verschiedene Art, da sonst keine Elektroneutralität erzielt werden kann: |
| |
 |
 |
| NaCl-Kristallstruktur |
CaF2-Kristallstruktur. Rot
= F-
(Linien ohne Bedeutung) |
|
|
 |
Wir erwarten relativ große Bindungsenergien und damit keine ganz niedrigen
Schmelzpunkte. Für E-Modul, thermischer Ausdehnungskoeffizient, maximale Bruchspannung
etc. interessieren wir uns nicht mehr so besonders, das haben wir bereits abgehakt. |
 |
Wir schauen uns jetzt erstmals
elektrische und optische
Eigenschaften an. |
|
 |
Wir wissen aus dem täglichen Leben: (Perfekte) Ionenkristalle sind durchsichtig
und Isolatoren. Die Frage ist: Warum? |
|
 |
Die Antwort ist: Sie haben keine freien Elektronen,
d. h. Elektronen, die im gesamten Kristall herumlaufen können, also nicht mehr fest an ein Ion gebunden sind. |
 |
Wir merken uns schon mal: |
| |
|
Lichtabsorption in Kristallen = Energie- und Impulstransfer vom Photon ("Lichtteilchen")
an ein freies Elektron | |
Elektrische Leitung im Kristall = Bewegung freier
Elektronen im elektrischen Feld |
|
|
|
 |
Aha! Deswegen sind alle guten Leiter (d. h. Metalle und ???) undurchsichtig!
(Zu Ausnahmen wie den durchsichtigen Leitern, die wir für flache Bildschirme und
Solarzellen brauchen, kommen wir später). |
 |
Braucht die ET&IT Ionenkristalle? Die einfachen wie NaCl eher
nicht. Die etwas komplizierteren aber schon (kommt noch). |
|
| |
 |
Hier die Aufgaben: |
|
|
|
© H. Föll (MaWi für ET&IT - Script)