2.1.4 Mixed Point defects

2.1.4 Mixed Point Defects

	Here we treat the most general and still sensible case of point defects in simple ionic crystals of the type AB.
		You may want to look up the illustration of the various possibilities before you proceed.
	We consider the simultaneous occurrence of Frenkel and Schottky defects, or the simultaneous occurrence of two kinds of vacancies and one kind of interstitial. This is the realistic general case because you may always safely neglect one of the two possible kinds of interstitials in equilibrium.
		This case is most elegantly treated invoking a "chemical" reaction equation and the mass action law. As mentioned before, you must be aware of the snares of this approach. Lets see this by writing down a reaction equation describing first the formation of a Frenkel pair in NaCl. This reaction must be able to go both ways, i.e. it must describe the generation and the annihilation of Frenkel pairs.
		Essentially, a positively charged cation, here a Na⁺ ion "jumps" in an interstitial site, leaving behind a (negatively charged) vacancy on a Na lattice site, denoted V_Na or cation vacancy and generating a (of course positively charged) Na⁺ interstitial, denoted Na_i or cation interstitial.

Now you may be tempted to write this down in a first reaction equation as follows

0 Û Na_i + V_Na

While this is not necessarily wrong, it is at least strange: You create, in a kind of chemical reaction, something from nothing - what keeps you from applying this equation to vacuum, which is surely not sensible? Maybe you should somehow get the crystal involved as the reference system within which things happen?

So let's device a more elaborate system by looking at our crystal before and after a Frenkel pair was formed

Before a Frenkel pair is formed, the site occupied by the vacancy after the formation process is a Na site, we denote it by Na_Na. This simply means that a Na atom occupies a Na site before a vacancy is formed there.

At the interstitial site, where the Na interstitial after the formation process is going to be, you have nothing before the process. However, all those possible interstitial sites also form a lattice (e.g. the lattice of the octahedral sites); in a perfect crystal all those sites are occupied by vacancies, we consequently denote an empty interstitial site by V_i = vacancy on an interstitial site.

A Na ion on an interstitial site then is Na_i, and a Na vacancy becomes V_Na . Now we can write down a reaction equation that reads

Na_Na + V_i Û Na_i + V_Na

This looks like a cool reaction equation, we now create a Frenkel pair within a crystal and not out of thin air.

Indeed, the reaction equation does look so much better this way! Small wonder, we just invented part of the so-called Kröger-Vink notation, in use since the fifties of the 20th century - not all that long ago, actually.

This notation is also called notation by structure elements and it is very useful for formulating all kinds of reactions involving point defects. However, the first law of economics applies ("There is no such thing as a free lunch"):

Don't use the mass action law uncritically with these kinds of reaction equations!. The reason for this is simple, but usually never mentioned in the context of chemical reaction formulation:

A proper reaction equation contains only reaction partners that are independent

This means that you can, in principle, change the concentration of every reaction partner without changing the others.

Consider for example the following purely chemical simple reaction equation:

2H₂ + O₂ Û 2 H₂ O

You can put arbitrary amounts of all three reaction partners in a container and change any individual amount at will without changing the others.

In our reaction equation for point defects, however, you cannot do this. If you consider, e.g., to change the Na_Na concentration a little, you automatically change V_i, too - those quantities are not independent!

This was the bad news about using Kröger-Vink notation. The good news are: In most practical cases it doesn't matter! Chapter 2.4 - often alluded to - will contain details about all of this.

It is not easy to grasp the reaction equation concept for point defects in all its complexity, but it is worthwhile if you want to dig deeper into point defects. For the purpose of this paragraph let's just postulate that the two sums left and right of the reaction equation would constitute the proper reactants (those sums, by the way, are called building elements in the Schottky notation).

Be that as it may, we now apply the mass action law, keeping in mind that the reaction equation from above in full splendor actually contains a reaction enthalpy G_Reaction, i.e.: Na_Na + V_i + G_Reaction Û Na_i + V_Na)

[Na_Na] · [V_i] [Na_i] · [V_Na]	= const = exp	G_Reaction kT

[Na_i] · [V_Na]	=	[Na_Na] · [V_i]	· exp –	G_Reaction kT

G_Reaction, of course, is the free enthalpy change of the crystal upon the formation of one mol of Frenkel pairs. If we relate it to 1 Frenkel pair, it becomes H_FP.

The [...] are the molar concentrations of the respective quantities if we use molar reaction enthalpies.

OK, now let's spell it out. If we have a crystal with N mols of NaCl, we have the molar concentration of [Na_Na] = N for really obvious reasons.

[V_i] = N, most likely, will hold, too, but here we may have to dig deeper. How many different places for interstitials do we have in the given unit cell? We can figure it out, but for the sake of generality their molar concentration could be larger or N' - so it can be different in principle from N as we have seen before.

Since we usually go for atomic concentrations, we note that c_V(C) = atomic concentration of the cation-vacancy = [V_Na] /N and c_i(C) = atomic concentration of the cation-interstitial = [Na_i] /N we now obtain one equation for the two unknowns c_V(C) · and c_i(C), which will be the first of the equations we will need for what follows.

c_V(C) · c_i(C)	=	N' N	· exp –	H_FP kT

(1)

Note that this is not our old result, because it does not imply that c_V = c_i. All the mass action law can do is to supply one equation for whatever number of unknowns.

We need a second independent equation. This is - of course (?) - always electroneutrality. Looking just at Frenkel pairs, we have directly

c_V(C)	=	c_i(C)

for Frenkel Pairs only

Now we have two equations for two unknown concentrations that we could easily solve.

However, we are interested in mixed defects here, so we must also consider Schottky defects and then mix them with Frenkel defects, always maintaining electroneutrality.

We might now go through the same procedure as before by using a similar reaction equation for Schottky defects - with a few more complications in finding the proper reaction equation. We will not do this here (do it yourself or use the link), just note the rather simple result:

With c_V(A) and c_V(C) denoting the vacancies on the anion or cation sublattice, resp., and with H_S = formation enthalpy of a Schottky pair, we obtain for a second equation

c_V(A) · c_V(C)	= exp –	H_S kT

(2)

Again, this is not the old equation for Schottky defects - the concentrations are not necessarily equal once more

Note that the vacancies on the anion or cation sublattice are positively or negatively charged - opposite to the charge of the (negatively charged) anion or (positively charged) cation that was removed! A cation vacancy thus carries a negative charge and so on, whereas a cation interstitial carries a positive charge. Look at the illustrations if you are not clear about this!

Knowing that electroneutrality has to be maintained (look at the direct calculation for Schottky defects), we introduce electroneutrality now for the more general case of our three charged defects: The sum of all charges on the point defects must be zero; we obtain the third equation

c_V(C)	=	c_V(A) + c_i(C)

(3)

Or: Sum over all negative charges = Sum over all positive charges.

Now we have 3 equations for 3 unknown concentrations, which can be solved with ease (haha). We obtain for the general situation of mixed defects

	c_V(C)	= exp –	H_S 2kT	·	æ ç è	1 +	N' N	· exp	H_S – H_FP kT	ö ÷ ø	1/2

	c_V(A)	= exp –	H_S 2kT	·	æ ç è	1 +	N' N	· exp	H_S – H_FP kT	ö ÷ ø	– 1/2

	c_i(C)	=	N' N	· exp	H_s 2kT	· exp –	H_FP kT	·	æ ç è	1 +	N' N	· exp	H_S – H_FP kT	ö ÷ ø	– 1/2

These equations contain the "pure" Frenkel and Schottky case as limiting cases.

Was that worth the effort? Probably not - as long as you just look at simple ionic crystals (where one defect type will prevail anyway). being in simple equilibrium without considering surfaces and the environment.

However! In real life, where point defects in ionic (and oxide) crystal are used for sensor applications, this kind of approach is the only way to go! It will be far more complicated, there will be approximations and "short-cuts", but the basic kind of reasoning will be the same.

Now it is time for an exercise

Exercise 2.1.5
Do the math and solve equations (1) - (3)

We now have the general equations and thus can answer the essential question for this case: How likely is a mixed case?

In a more quantitative fashion we ask: How different must the formation enthalpies be if just one defect type should dominate?

That is, of course, an excellent exercise question.

Exercise 2.1.6
Enthalpy difference for the limiting cases

If you do the exercise, you will find out that relatively small differences in the order of 0.1 eV in the formation energies of Schottky or Frenkel defects will already lead to the preponderance of one defect type.

This is important! Since it is quite likely that formation enthalpies for Schottky or Frenkel defects in a given crystal will differ by more than just 0.1 eV, we are quite justified to look at the defect situation in an "either - or" mode: "Either we will have Frenkel defects, or Schottky defects. One kind will practically always "win".

The final questions are then: When do we have Schottky disorder, when do we have Frenkel disorder? What are typical formation enthalpies? Are there general criteria for what kind is more likely to occur in a given crystal? Can we tell or at least make an educated guess?

Well let's look at a few experimental findings (all numbers are from "Hayes and Stoneham" ; more numbers can be found in the link):

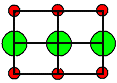
Crystal	Type of lattice	Type of disorder	Formation enthalpies H_S/F [eV]		<110> projection Ion size to scale
Crystal	Type of lattice	Type of disorder	Formation enthalpies H_S/F [eV]		Cations = red Anions = green
NaCl and all other alkali halides	NaCl-type	Schottky	LiF	2,5	projection" TITLE="click to enlarge size">
			NaCl	2,3
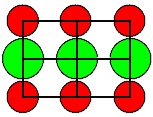
			KCl	2,3
			KBr	2,4
			CsI	1,9	projection" TITLE="click to enlarge size">
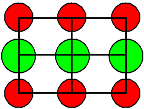
Some Oxides			MgO	5,7
AgCl and AgBr,	NaCl-type	Frenkel with cation interstials	AgCl	1,45	projection" TITLE="click to enlarge size">
NaNO₃, KNO₃, ..	complex	Frenkel with cation interstials
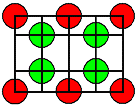
CaF₂ and SrF₂, BaF₂	CaF₂ type	Frenkel with anion interstials ("Anti-Frenkel")	CaF₂	2,7
			SrF₂	2,3
			BaF₂	1,9	projection" TITLE="click to enlarge size">
			SrCl₂	1,7

What we see is:

1. It is hard to make a prediction of what kind of defect you will find. Even looking at a lattice projection with the ions drawn to scale (using tabulated ionic radii) does not offer immediate clues (besides the obvious one that you only would expect Anti-Frenkel defects with anion interstitials, if the anion is not much larger than the cation).

2. The formation enthalpies of Frenkel defects tends to be a bit lower than those of Schottky defects.

3. The formation enthalpies in the more simple ionic crystals (no oxides) tend to be rather small - around 1 eV per single defect; quite comparable to the vacancy formation enthalpy of simple metals. This might be taken as a hint that charge matters less than bonding and lattice distortion.

Exercise 2.1-8
Quick Questions to 2.1.2 - 2.1.4

	One more word of warning: Be careful in applying mass-action laws!
		If you would, e.g., attempt to carry over the results obtained here to Si (because its the only known elemental crystal where interstitials occur in sizeable quantities), you would be making a mistake, because the reaction equation describing the formation of Frenkel pairs given above is not the right equation for Si.
		The reason for this is that your independent quantities are different: You may add vacancies without changing the interstitial count because electroneutrality in a semiconductor may be achieved by changing electron or hole concentrations and you must not only balance charged point defects against each other.
		In addition, never forget that chemical reaction equations always demand that there are no other reactions (e.g. parasitic reactions) that consume non-negligible quantities of the reactants. What about other crystal lattice defects? A vacancy, after all, may disappear at a dislocation; causing the dislocation to climb; or it may react with precipitates. Some precipitates even need vacancies in order to be to be able to grow. Others emit interstitials while growing - you must include those reactions in your description of the system if it is to be correct.