 |
It is important to be clear about the possibilities of producing
defects in ionic crystals. It is also important to be clear about names:
- Anions move to a positively charged electrode
also called anode, they are therefore negatively
charged particles. Examples: The Cl– ions in NaCl.
- Cations move to a negatively charged electrode
also called cathode. Example: The Na+ ions in NaCl,
|
| |
 |
Now there is some room for confusion: If we take out the negatively charged cation Na+,
we have produced a cation vacancy that has a positive effective charge and thus behaves
like an anion! |
|
 |
Here is all that can happen in a simple NaCl crystal: |
| | |
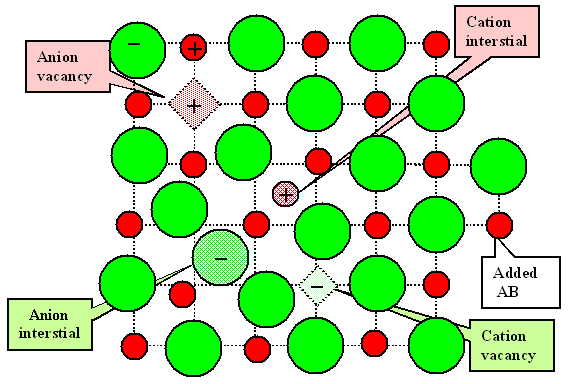 |
| "General" Disorder |
|
| |
 |
Even for the most simple ionic crystals of the type A+B– like LiCl
or NaCl, we can, in principle, produce arbitrary concentrations of two kinds
of vacancies and two kinds of interstitials as shown on the left.
However, as we already learned in dealing with Schottky defects, global charge
neutrality must be maintained. Arbitrary concentrations are thus not really
allowed, we must demand that the the sum of the positively charged defects equals the
sum of the negatively charged defects. In other words: we have to obey the charge conservation
law. |
| |
 |
If we also keep the number of atoms constant, we must add an A or B atom to the surface of
the crystal for every pure vacancy we produce. In other (fancy) words, we have to obey the mass
conservation law. |
| |
 |
The picture on the left would not have needed the AB molecule, because we have two interstitials,
too. But since it is supposed to illustrate the general case, with arbitrary numbers
of defects, it needs to include A and B atoms on the surface. |
| | | |
|
 |
As always, you must bear in mind that pictures as shown here are schematic
- in more realistic pictures the ions would touch! However, in more realistic pictures it also would be harder to show what
is intended. |
|
 |
This will always be true if the anion is larger as the cation which is the case for many, but not all ionic
crystals. We thus can safely assume that the concentration of one kind of interstitial,
here the anion interstitial, is always far smaller than that of the
other three defect kinds and we will simply neglect it from now on. |
|
 |
However, for crystals with a big and heavy cation (e.g. Ca+) and a light anion (e.g.
F–), the cation might just be as big as the anion, and occur as interstitial (e.g. in the so-called
"Anti-Frenkel defects"). |
| | |
 |
If we forget about the anion interstitial, we are left
with three possible point defects. |
| |
|
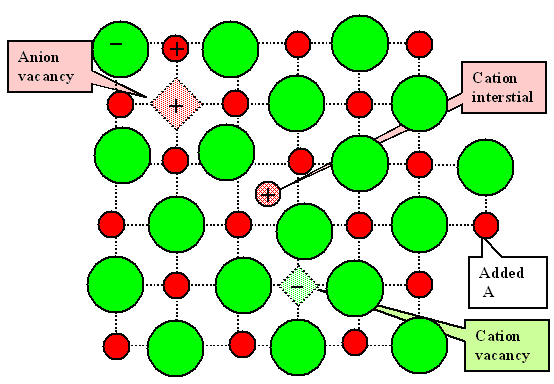 |
| Realistic Disorder |
|
| |
 |
The three now possible defect types are shown on the left. This is the general case of the
mixed defects treated in the backbone |
| |
 |
Note that charge equilibrium demands that you always have more
cation vacancies than anion vacancies or cation interstitials: |
| | |
|
| |
 |
This necessitates that some AB molecules must be added to the surface of the crystal if we keep
the atom count in order, too (same concentration as the anion vacancy, to be precise). |
 |
The realistic mixed case thus contains Schottky
and Frenkel defects in parallel. |
|
 |
Note that the picture above does not show the equilibrium case, because
we do not have charge neutrality - for that it would need another cation vacancy. |
|
 |
Every cation vacancy finds an anion vacancy as a fictive partner, forming a formal Schottky defect, and
every cation interstitial finds a cation vacancy, too, for a formal Frenkel pair, and the concentration of the anion vacancies
is just so that it meets both demands for partners. |
|
 |
We thus can identify cV(A) with the concentration of Schottky defects and ci(C)
with the concentration of Frenkel defects. |
|
|
 |
Schottky and Frenkel disorder may now simply be seen as extreme
cases of the mixed disorder. |
| | |
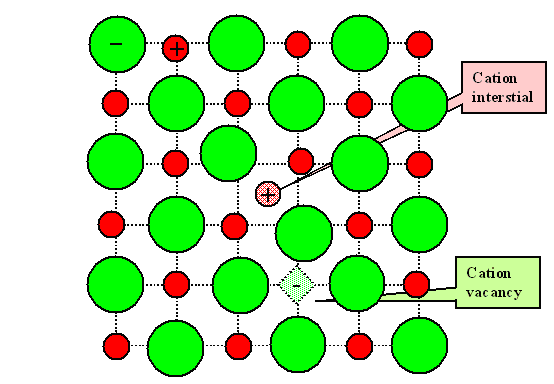 |
| Frenkel disorder |
|
|
 |
Frenkel disorder is predominant if the formation enthalpy
of Frenkel pairs is smaller than that of Schottky pairs, i.e.
HFP < HS |
| |
We then only - or at least predominantly - have Frenkel pairs, i.e. equal numbers of cation vacancies and
cation interstitials. We do not have an AB molecule for Frenkel disorder. |
| | |
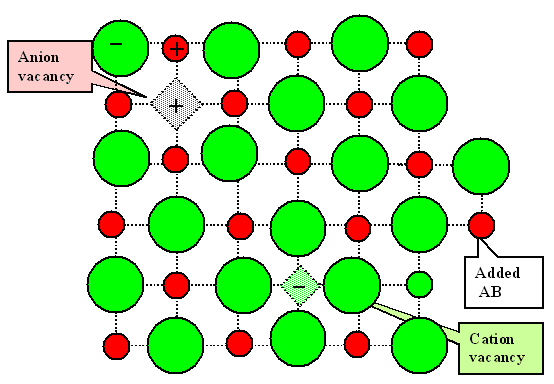 |
| Schottky disorder |
|
| |
Schottky disorder is predominant if the formation enthalpy of Schottky
pairs is smaller than that of Frenkel pairs, i.e.
HS < HFP. |
| | |
We only - or at least predominantly - have vacancy pairs, i.e. equal numbers of cation vacancies
and anion vacancies. And - in contrast to Frenkel disorder - we always need to form a lattice molecule, our AB
molecule, to preserve atom numbers. |
 |
Just how much smaller the relevant formation enthalpy has to be for factual predominance of
one defect type remains to be seen - in an exercise. |
| |
© H. Föll (Defects - Script)



