Octahedral Sites

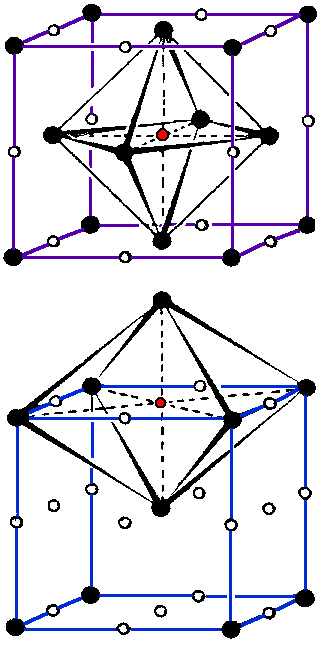
An octahedral position for an (interstitial) atom is the space in the interstices between 6 regular atoms that form an octahedra.
Four regular atoms are positioned in a plane, the other two are in a symmetrical position just above or below. All spheres can be considered to be hard and touching each other.
The six spheres define a regular octahedra, in its interior there is a defined space for an interstitial atom, bordered by six spheres.
Octahedral sites exists in fcc and bcc crystals. The other prominent geometric environment for interstitials is the tetrahedral site.

This illustration shows the octahedral site in an fcc lattice bottom. We have 12/4 +1 = 4 positions per unit cell.
Here we have octahedral sites in the bcc lattice. We have 12/4 + 6/2 = 6 positions per unit cell.
   

With frame With frame as PDF

go to 1.3.3 The larger View and Complications

go to 2.1.1 Simple Vacancies and Interstitials

go to Interstitials

go to Tetrahedral Sites

go to Ionic Crystals

go to 2.1.4 Mixed Point defects

© H. Föll (Defects - Script)