2.1.4 Vom Bindungspotential zum Kristall

Richtungsabhängigkeit der Bindung

	Falls es zwischen 2 Atomen ein Bindungspotential mit einem Potentialtopf gibt, möchten die beiden eine Bindung eingehen – zumindest bei Temperaturen, die tief genug sind.
	Wenn sich nun ein A-Atom nach B-Partnern umschaut, gibt es zwei grundsätzliche Möglichkeiten, wie es sich mit B paaren kann: Die Richtung, in der sich B von A aus gesehen befindet, ist egal; das Bindungspotential ist richtungsunabhängig. Die Richtung, in der sich B von A aus gesehen befindet, ist nicht egal; das Bindungspotential ist richtungsabhängig.
		Der erste Fall entspricht der Polygamie. A macht alle erreichbaren B-Atome an, egal wo, und will sie möglichst dicht (im Gleichgewichtsabstand r0) und fest (mit UBdg) an sich binden. Grenzen sind nur durch die Geometrie gesetzt. Sobald A komplett von B's umgeben ist, können keine weiteren B's mehr gebunden werden, wie im (meist zweidimensionalen) Beispiel unten gezeigt.
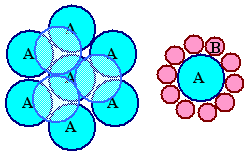
		Struktur bei ungerichteter Bindung Struktur bei gerichteter Bindung
	Gezeigt ist der homoerotische Fall in beiden Gruppen – A tut sich mit A zusammen – sowie eine denkbare Heterosituation im Falle der ungerichteten Bindung. Klar ist:
		Im Falle der ungerichteten Bindung geht die Anhäufung von Atomen immer weiter; in der Fläche und nach oben und unten – angedeutet ist der Beginn einer 2. Lage oben links. Grundsätzlich erwarten wir dafür eine dichteste Kugelpackung. In Kristallen mit ungerichteten Bindungen – egal ob aus 1, 2, 3 oder n Atomsorten – sollten sich die (i.a. verschieden großen) Kugeln immer so anordnen, dass möglichst viele im gegebenen Volumen sind (die Gesamtladung aber bei Ionen = 0 bleibt).
		Im einfachsten Fall einer Atomsorte ist die räumliche Anordnung damit also klar – oder? "Oder" ist richtig, wir kommen darauf zurück. Vorher darf aber jede mal selbst probieren, ob sie die bestmögliche Anordnung fndet (z. B. mit Tischtennisbällen oder Orangen).
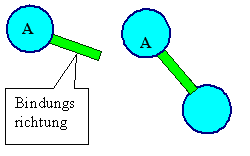
	Falls das Bindungspotential gerichtet ist (so daß die Parameter A, B, m, n Funktionen von Winkeln sind), betrachten wir schlauerweise nur die eine, zwei, oder maximal wohl um die 12 Richtungen (ja, 12 – aber warum 12 und nicht bloß 6 oder 8?), in denen das Potential die tiefsten Minima hat. In diese Richtungen malen wir dann "Bindungsarme" als Striche.
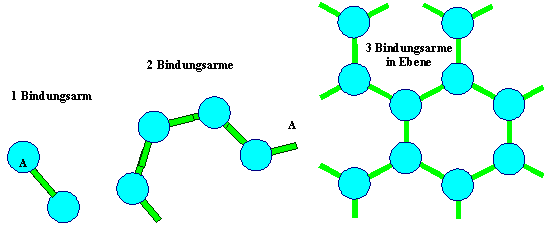
		Falls es mehr als einen Bindungsarm gibt, kann ein zusammenhängendes Gebilde entstehen (das Wort "Kristall" ist hier bewußt vermieden).
		Für die gezeigten Fälle mit einem, zwei oder drei (koplanaren) Bindungsarmen bekommen wir notgedrungen ein Gas , lange Ketten oder einen zweidimensionalen Kristall (= atomare Schicht).
	Frage: Kann man bei drei Bindungsarmen eine dreidimensionale Struktur aufbauen?
		Wir lassen die Frage mal offen (die Antwort kommt später ), sind uns aber sicher, dass es mit 4 (nicht koplanaren) Bindungsarmen geht:

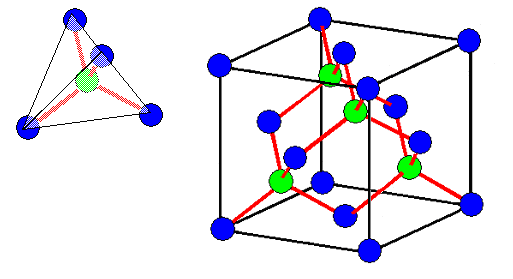
	Das grüne Atom hat 4 Bindungsarme, die sich untereinander maximal "abstoßen". Dann bleibt ihnen nichts anderes übrig, als in die Ecken des Tetraeders zu zeigen, in dessen Mitte das Atom sitzt.
		Die Winkel zwischen den Bindungsarmen sind dann gleich groß und maximal, d. h. gleich dem Tetraederwinkel von ???? o. Bindet sich ein Atom mit ebenfalls tetraedischer Bindungsarmsymmetrie (im Zweifel eines der gleichen Sorte), liegt die dreidimensionale Kristallstruktur fest – eben so wie oben gezeigt. Interessanterweise kann man einen Würfel finden, der irgendwie dazu paßt.
		Diese Kristallstruktur steht im Zentrum der Elektronik – denn in dieser "Diamantstruktur" kristallisieren fast alle wichtigen Halbleiter (und der Diamant, also Kohlenstoff), insbesondere Silizium!
	Die Schlußfolgerungen sind klar: Die Richtungsabhängigkeit des Bindungspotentials bestimmt: Ob es überhaupt Kristalle gibt. Die Struktur: Entweder dicht gepackt oder sehr spezifisch. Vorhersagen sind nicht automatisch leicht; und das gilt selbst für die einfachsten Fälle.
		Der letzte Punkt braucht vielleicht noch eine Erläuterung: Obwohl es nie den geringsten Zweifel gab, wie man gleichgroße Kugeln am dichtesten packen kann (das macht jeder und jede automatisch so wie oben gezeigt), hat die harte Mathematik Jahrhunderte gebraucht um zu beweisen, dass diese Struktur in der Tat die am dichtesten gepackte ist!
	Trotzdem, nochmal: Die Grundeigenschaften eines Atoms bestimmen wie es mit anderen Atomen bindet, d. h. das Bindungspotential. Daraus folgt zwingend die Struktur des Festkörpers und viele seiner Eigenschaften.
		Es wird Zeit, Bindungen etwas näher anzuschauen.
	Aber erst mal ein paar schnelle Fragen:
		Fragebogen Einfache Fragen zu 2.1.4

© H. Föll (MaWi für ET&IT - Script)