Übung 2.1-3

Schwingungsfrequenz der Bindung

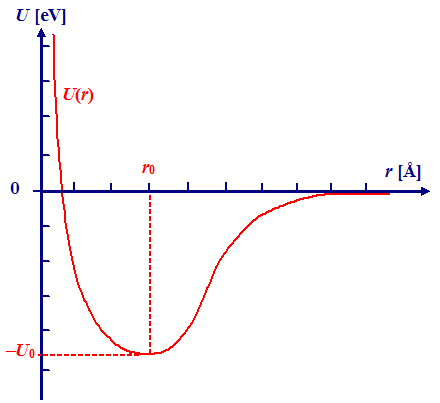
	Gegeben sei ein Bindungspotential der Form
		U  =    –  A r n  +   B r m
	Damit wir damit einfach rechnen können, ersetzen wir das komplette Potential durch eine Taylor Entwicklung bis zum quadratrischen Term um das Minimum (bei r := 0):
		U  =  U0 + 1/2U0''  · x2           mit           U''(r0 )  =  U0 · (nm/r02 )
	Frage 1: Zeige dass das obige Ergebnis für die zweite Ableitung von U korrekt ist.

	Die generelle Bewegungsgleichung mit der Lösung für die Resonanz- oder Eigenfrequenz einer harmonischen Schwingung lautet
		ma ·  d2x dt2  +  kFed · x  =  0
		mit ma = Masse des oszillierenden Atoms und kFed = "Federkonstante"
		Für die Eigen(kreis)frequenz w der Schwingung gilt
		w  =    æ ç è kFed ma ö ÷ ø ½               w  =  1 r0 æ ç è U0· n · m ma ö ÷ ø ½
	Frage 2: Leite die erste Gleichung für w her und zeige dann, dass in der Tat für die Federkonstante kFed = r0 –2 · U0· n · m gilt.

	Wenn wir uns jetzt noch an die bereits abgeleitete Beziehung für den Elastizitätsmodul erinnern, können wir w auch wie folgt ausdrücken:
		w  = æ ç è E · r0 ma ö ÷ ø 1/2
	Frage 3: Zeige, dass obige Gleichung stimmt.
	Frage 4: Bestimme damit die Größenordnung für w für einige einfache Materialien.
		Hinweis: Werte für den E-Modul findet man im Skript. Die Masse der Atome sollte auch leicht auffindbar sein
	Frage 5: Was für Konsequenzen könnten sich daraus für die Wechselwirkung von "Wechselstrom" (in Form einer hochfrequenten elektromagnetische Welle) und dem Material ergeben?

	Lösung

Mit Frame

2.1.3 Bindungspotentiale und weitere Eigenschaften

Übung 2.1-1

Lösung Übung 2.1.2-2

Lösung Übung e2.13

© H. Föll (MaWi für ET&IT - Script)