6.4.2 Der Frequenzgang der (komplexen) Dielektrizitätskonstante für Resonanz

Die Resonanz im gewohnten Bild

	Falls wir die Grenzflächenpolarisation "vergessen", sind zwei der drei verbleibenden Mechanismen dadurch gekennzeichnet, daß das elektrische Feld an den vorhandenen geladenen Massen zieht, während eine "Federkraft", d. h. eine Kraft proportional zur Auslenkung, sie zurückzieht.
		Bei der Atompolarisation kam die Federkraft aus der Coulomb Anziehung zwischen "verschobener" Elektronenwolke und Atomkern (weshalb die Atompolarisation auch Elektronenpolarisation heißt), bei der ionischen Polarisation durch die Bindungs"feder".
		Falls das elektrische Feld und damit die externe Kraft mit der Kreisfrequenz w oszilliert, werden die ladungsbehaften Massen eben periodisch getrieben.

	Das ist nichts Neues – hat die Physik schon mal gemacht. Sie hat das Ganze sogar noch ein bißchen komplizierter gemacht, indem sie noch "Reibung" berücksichtigte.
		Reibung ist hier nur ein anderes Wort für Dämpfung, d. h. für den Effekt, daß kein Oszillator ewig vor sich hinschwingen wird, falls man ihn alleine läßt.
		Grundsätzlich betrachten wir ein System wie im nebenstehenden Bild dargestellt.
		Wir haben eine Masse m an einer Feder, die noch eine Ladung q trägt.
		Wird die Masse um den Betrag x ausgelenkt, wird eine Feder mit der Federkonstante kF eine Rückstellkraft FFeder produzieren; wie immer berücksichtigt das Minuszeichen, daß die Kraft der Auslenkung entgegenwirkt:
		FFeder  =  –kF · x
		Die Dämpfung berücksichtigen wir, indem wir eine Reibungskraft FR einführen, die proportional ist zur Masse m, der Geschwindigkeit dx/dt und einem Reibungs- oder Dämpfungskoeffizienten kR. Auch hier drückt das Minuszeichen aus, daß die Kraft der Bewegung entgegenwirkt:
		FR =  –kR · m · dx/dt

	Fertig. Mit F = m · d2x/dt2 erhalten wir sofort die Differentialgleichung, deren Lösung uns alles gibt, was wir wissen wollen:
		m · d2x dt2  +  kR · m · d x d t  +  kF · x   =  q · E0 · cos(wt)
	Mit den Lösungen zu dieser Differentialgleichung hat die Physik uns schon hinreichend intensiv gequält; wir schreiben sie deshalb gar nicht hin, sondern schauen uns nur die graphische Darstellung an und erinnern uns an die wesentlichen Punkte:
		Im ungedämpften Fall (kR = 0 s–1) steigt die Amplitude bei der Resonanzfrequenz w0' über alle Grenzen; gleichzeitig springt die Phase von 0° auf 180°. Für die Resonanzfrequenz gilt:
		Ohne Dämpfung w0'  =  æ ç è kF m  ö ÷ ø 1/2 Mit Dämpfung w 0  =  æ ç è kF  m   –  kR2 4  ö ÷ ø 1/2
		Mit Dämpfung ist die Resonanzamplitude endlich; sie wird mit zunehmender Dämpfung kleiner. Gleichzeitig macht die Phase keinen Sprung mehr sondern ändert sich im Resonanzbereich stetig – so wie im Bild gezeigt.
	Die Dämpfung sorgt auch dafür, daß die Amplitude einer Schwingung nach Wegnehmen der treibenden Kaft exponentiell abklingt. Das sieht in Formeln und in Bildern so aus:
		x(t)  =  x0 · cos(w0t) · exp æ ç è – kR 2   · t ö ÷ ø
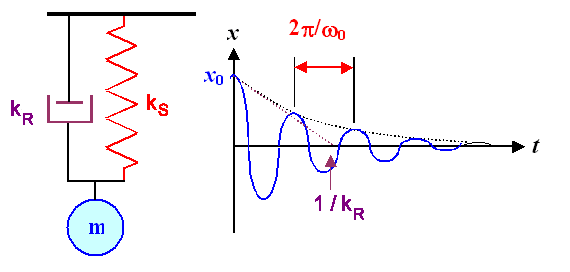
		Das sollte man etwas verinnerlichen, denn die Graphik (wie auch schon die Formel) sagt uns, wie man ein Gefühl für die Größe der Dämpfung entwickeln kann: Der Kehrwert der Dämpfungskonstante gibt an, nach welcher Zeit dieSchwingung so in etwa abgeklungen ist. Damit sagt uns w /kR so rund und roh, wie oft das System nach dem Abschalten noch hin und her zappelt. Das werden wir gleich noch mal brauchen!

	Die Resonanz in komplexer Darstellung
	Wir wollen eigentlich die Frequenzabhängigkeit der komplexen DK erhalten, und deshalb betrachten wir jetzt exakt dasselbe noch mal in komplexer Schreibweise.
		Die grundlegende Differentialgleichung lautet:
		m · d2x dt2  +  kR · m · d x d t  +  kF · x   =  q · E0 · exp(iwt)
		Die Lösung lautet (der Stern *  kennzeichnet lediglich eine komplexe Zahl):
		Ansatz x*(w, t)   =   x*(w ) · exp (iwt) Allgemeine Lösung x(w)  =   q · E0 m æ ç è æ è w02 – w2 (w02 – w2)2 + kR2 w2 ö ø   –  i · æ è kR w (w 02 – w 2)2 + kR 2 w2 ö ø ö ÷ ø Realteil der allg. Lösung   x'(w)  =   q · E0 m æ ç è w02 – w 2 (w02 – w 2)2 + kR2 w2 ö ÷ ø Imaginärteil der allg. Lösung   x''(w)  =   q · E0 m æ ç è kR w (w02 – w2)2 + kR 2 w2 ö ÷ ø
	Wow! Diese Gleichungen muss man aber nicht wissen – nur ihre prinzipielle graphische Darstellung! Die sieht so aus:
	Was ist der Unterschied zwischen der direkten Darstellung und der komplexen Darstellung? Das kann man am besten in einem Zeigerdiagramm sehen:
		Ob ich den Zeiger, der die Lösung markiert, über seine Länge und den Phasenwinkel beschreibe oder über seien Real- und Imaginärteil, bleibt sich gleich. Es gibt kein "Richtiger" oder "Besser". Was man wählt ist eine reine Frage der Zweckmäßigkeit; umrechnen kann man immer.

	Die dielektrische Funktion bei Resonanzmechanismen
	Haben wir die Amplituden, haben wir auch die Dipolmomemte . Haben wir die Dipolmomente, bekommen wir die Polarisation, daraus die Suszeptibilität und schließlich und endlich die dielektrische Funktion.
		Für jeden resonanten Mechanismus lautet sie (gleich für Realteil und Imaginärteil getrennt geschrieben) wie folgt:
		e'  =   e 0  +   N · q2 m     æ ç è w02 – w2 (w02 – w2)2  +  kR2 · w2 ö ÷ ø               e ''  =   N · q2 m   æ ç è kR · w (w 02 – w2)2  +  kR2 · w2 ö ÷ ø
	Geil? Nein, denn um rechnen zu können (oder auch nur um abschätzen zu können), brauchen wir: Zahlenwerte für die Federkonstante (sie steckt in der Resonanzfrequenz w0). Zahlenwerte für den Dämpfungskoeffizienten kR. Ein Gefühl dafür was passiert wenn da nicht nur ein Atom ist, sondern ein großer, irgendwie durch Federn gekoppelter Haufen.
	Die Liste sieht komplizierter aus als sie ist. Also:
	1. Problem: Ist kein Problem, denn für die ionische Polarisation haben wir die Federkonstante kF = Y · a mit Y = E-Modul Y; a = Gitterkonstante. Für die Atompolarisation haben wir sie nicht, aber sie ist leicht auszurechnen.
	3. Problem: Hängt mit dem 2. Problem zusammen, deshalb behandeln wir es zuerst.
		Obwohl man meinen konnte, daß die Schwingerei von sehr vielen gekoppelten Massen sehr kompliziert sein sollte, ist es kein wirklich schwieriges Problem. Denn:
		Haben wir nur eine Atomsorte und wackeln gedanklich mal nur an einem Atom des Kristalls, so wirkt es auf seine (bis zu 12 bei dichtester Kugelpackung) Nachbarn jetzt wie die antreibende Kraft. Die Nachbarn werden ebenfalls anfangen zu oszillieren, sie treiben dann ihre bis zu 144 Nachbarn an, und so fort. Ziemlich schnell schwingen alle Atome, mehr oder weniger mit der Resonanzfrequenz des Einzeloszillators – aber mit winziger Amplitude.
		Denn die gesamte Energie, die zunächst in der Schwingungsamplitude des einen Atoms steckte, hat sich jetzt auf furchtbar viele verteilt – und das sogar noch recht schnell. Was bedeutet das? Wir haben das 2. Problem schon geknackt:
		Haben wir Atome mit verschiedenen Massen im Kristall, schwingen diese eben ein bißchen verschieden, das Ergebnis ist eine Überlagerung der diversen Schwingungsmoden (so nennt man das). Statt nur einem Ton (= Frequenz) kommen jetzt halt mehrere aus der Flöte – sorry, aus dem Kristall.
	2. Problem: Die Schwingungen, die uns hier interessieren, sind immer sehr stark gedämpft; siehe oben. Man kann sich das auch so vorstellen:
		Man stelle sich einen Kristall vor, bei dem alle Atome ruhig dasitzen (z. B. bei 0 K). jetzt ziehen wie ein Atom etwas "raus" und lassen dann los. Es wird mit seiner Resonanzfrequenz schwingen, aber mit schnell abnehmender Amplitude, d. h. mit großer Dämpfung, da es sofort eine ganze (Halb)Kugelwelle losschickt, die in den Kristall hineinsaust – wie oben beschrieben. Die Anfangsenergie verteilt sich damit schnell auf immer mehr Schwinger.
	Was wissen wir jetzt über die dielektrische Funktion bei Resonanzphänomenen? Eine ganze Menge:
		Sie wird eher so wie die blaue oder grüne Kurve in der obigen Prinzipdarstellung aussehen. Oberhalb der Resonanzfrequenz geht der Realteil auf 1, d. h. das dielektrische Verhalten verschwindet (unsere "klassische" DK ist 1). Nur um die Resonanzfrequenz herum ist der Imaginärteil deutlich von Null verschieden – um so mehr, je größer die Dämpfung! Wir haben dann dielektrische Verluste, die wir uns noch genauer ansehen werden. Die Resonanzfrequenz bei der ionischen Polarisation kennen wir im übrigen schon. Es sind natürlich die berühmten ca. 1013 Hz, die wir generell aus dem Bindungspotential erhalten. Die Resonanzfrequenz bei der Atompolarisation haben andere für uns ausgerechnet. Bein Wasserstoffatom (größtmöglicher Effekt) liegt sie bei 5 · 1016 Hz, also im Ultravioletten. Damit ist klar: Es gibt keine "normale" Optik mehr im UV und darüber – alle Brechungsindizes sind n = 1
	Zeit für schnelle Fragen:
		Fragebogen Schnelle Fragen zu 6.4.2

© H. Föll (MaWi für ET&IT - Script)