|
In den vorangegangenen Moduln haben wir einerseits postuliert,
dass "Dielektikum" erstmal nur ein anderes Wort für Isolator
sei, aber andererseits Zahlenwerte für die DK von Halbleitern angegeben.
Was den nun? Halbleiter sind nun mal keine
Isolatoren; Standard-Si hat z. B. einen spezifischen Widerstand so um 1 Wcm. |
|
 |
Man darf also beim Begriff einer Dielektrizitätskonstanten für einen Halbleiter ein gewisses Puristenbauchweh bekommen.
|
 |
Es ist Zeit, nach der "erstmals" Definition das "zweitmal"
anzugehen. Beim zweiten Mal hat man ja auch schon ein bißchen Erfahrung; das kann dann sogar mehr Spaß bringen. |
|
 |
Für Halbleiter können wir uns im Prinzip noch einfach aus der Patsche
helfen: Wir kühlen das halbleitende Material. Spätestens in der Nähe
des absoluten Nullpunkts wird es ein guter Isolator sein. Dann kann man die DK in der gewohnten
Weise messen. |
 |
OK - aber das klingt ein bißchen künstlich. Deswegen machen wir jetzt
die folgende sehr allgemeine und ohne Tricks umsetzbare Überlegung: |
|
 |
Bei einem idealen Isolator im Plattenkondensator
fließt bei anliegender Gleichspannung oder besser Feldstärke keine Gleichstromdichte;
bei Wechselspannung ist die fließende Wechselstromdichte exakt 900 phasenverschoben zur Spannung.
Rein elektrisch haben wir dafür das Symbol 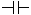 . . |
|
 |
Falls das Material rein "ohmsch" ist, also eine spezifische Leitfähigkeit
s = 1/r
¹ 0 hat, fließt Gleichstrom oder Wechselstrom in Phase (Phasenverschiebung
00). Dafür gibt's dieses Symbol  . . |
 |
Wir zerlegen jetzt gedanklich das Material in seinen ideal-dielektrischen Teil
und seinen nicht vernachlässigbaren ohmschen Widerstandsteil, d.h. beschreiben es so: |
| |
|
|
 |
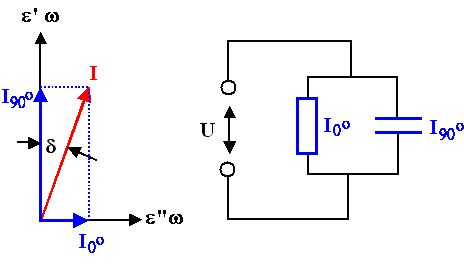
Wir haben einen idealen ohmschen Widerstand R parallel zu einem
idealen Kondensator C mit zugehörigem Zeigerdiagramm.
|
|
 |
Der Winkel d wäre für ein ideal isolierendes Dielektrikum d = 0o. Für
ein reales Dielektrikum mit R < ¥
W ist tgd = I0/I90 > 0.
Die resultierende Zahl, die ja bei Frequenzen im kHz Bereich oder so leicht zu messen ist, wird oft in Tabellen angegeben,
der sogenannte "Tangens Delta ist eine Art Qualitätsmaß für Dielektrika
/ Isolatoren. |
 |
An den Achsen des Zeigerdiagramms steht nun verwirrenderweise neben den Strömen
auch e' und e''. Was soll das bedeuten? |
|
 |
Na ja – wir schreiben mal die frequenzabhängige Stromdichte
j(w) durch einen Kondensator hin, der einem elektrischen Wechselfeld E
= E0 exp(iw t)
ausgesetzt ist. Das führt zu einer Verschiebungsdichte D = e
0 er(w) E. |
|
 |
Wir haben beim idealen Kondensator natürlich nur Verschiebungsströme,
d. h. j(w) = dD/dt . Dafür erhalten wir: |
| |
| j(w) = |
dD
dt |
= e0
er(w) |
dE
dt
|
= e0
er(w ) |
d[E0 exp(iw t)]
dt |
= e0
er(w) · i w ·
E0 exp (iwt) = e0
er(w) · i w · E(w ) |
|
|
 |
Die Phasenverschiebung von 90o steckt im i (mit i2
= –1). Materialwissenschaftler sind boshafte Menschen und verwenden für die imaginäre
Einheit den Buchstaben i und für die Stromdichte den Buchstaben j - genau andersrum als Elektrotechniker.
Wer jetzt darüber nachdenkt, wer "recht" hat, sollte was Einfaches studieren und Jurist werden. |
 |
Wenn wir jetzt ein beliebiges Realmaterial beschreiben wollen, das halt auch außer
seiner DK auch noch eine endliche Leitfähigkeit hat, d. h. zu seiner kompletten Beschreibung noch einen ohmschen
Widerstand parallel zum idealen, durch die DK beschriebenen Kondensator braucht, können wir das Ganze durch
einen simplen Trick erledigen: |
|
|
Wir nehmen für die (frequenzabhängige) Dielektrizitäts"konstante"
er die komplexe Zahl:
er(w) = e'(w) – i · e''(w) |
|
|
 |
Das Minuszeichen ist hier Konvention, damit
in der nachfolgenden Gleichung das bequemere + steht. Wir betrachten also den negativen Imaginärteil einer komplexen Zahl. |
 |
Das gibt uns eine simple Beziehung, die wir noch brauchen werden: |
| |
| j(w) | = |
e0 · w · e''(w) · E | + i |
e0 · w · e'(w) · E | | |
| | |
| | |
|
Realteil
von j(w) = j0;
Phase = 0o | |
Imaginärteil von
j(w ) = j90;
Phase = 90o |
|
|
 |
Das ist eine ziemlich coole Gleichung! Denn jetzt können wir auch für
ein beliebiges Material eine DK definieren! Wir nennen das dann auch nicht mehr
"Dielektrizitätskonstante
", wäre ja albern, sondern dielektrische Funktion. |
|
 |
Wir packen also einfach den Leiteranteil in den Imaginärteil der dielektrische Funktion eines Materials; der Realteil beschreibt dann die "klassische"
DK. |
|
 |
Wenn man da mal kurz darüber nachdenkt, kommt man zum folgenden Schluss: |
| |
In der (komplexen) dielektrischen Funktion eines Materials stecken alle
elektrischen und optischen Eigenschaften
des Materials. |
|
 |
Das ist doch was! Zwei Kurven – Real- und Imaginärteil über der
Frequenz – ist alles, was man braucht, um ein Material elektrisch und optisch vollständig zu charakterisieren!
Die dielektrische Funktion eins Materials gehört damit zwingend in die universitären Grundlagen der Materialwissenschaft
für Elektro- und Informationstechniker. |
|
 |
Na ja. Wenn man ganz genau hinschaut, endeckt man noch so ein paar Klauseln und
Nebenbedingungen Die sind aber für das Gesamtbild unwichtig und sollen uns hier nicht weiter interessieren. |
| |
|
|
Dielektrische Verluste |
| | |
 |
Wenn man Strom und Spannung multipliziert, bekommt man bekanntlich die im "Verbraucher"
umgesetzte Leistung L in Watt (W). |
|
 |
Wenn man Stromdichte und Feldstärke
multipliziert, bekommt man bekanntlich (?) die im "Verbraucher" umgesetzte
Leistungsdichte in Watt pro cm3 (W · cm–3). |
 |
Wenn Stromdichte und Feldstärke oszillieren,
muss man auf die Phasenbeziehung der beiden achten. |
|
 |
Man teilt dann die Stromdichte auf in den Teil j 0, der
in Phase fließt, und den Teil j90, der um 90o
phasenversetzt fließt; mit Zeigerdiagrammen geht das sehr einfach. |
|
 |
Dann gilt:
- Feldstärke mal j0 = LW
= Wirkleistung, wird meist in Wärme umgewandelt.
- Feldstärke mal j90 = LB = Blindleistung, macht weiter nichts.
|
 |
Gleich oben stehen Ausdrücke für beide Stromdichtekomponenten. Multipliziert
mit E(w) = E0 · exp (iwt)
erhält man die folgenden, auf das Volumen bezogenen Leistungsdichten: |
| |
|
|
|
 |
Fein. Das war wohl zu erwarten. Mit e' haben
wir ja die klassische DK beschrieben, die im Kondensator leistungsmäßig ja außer Blindleistung nichts
macht. Mit e'' haben wir den noch vorhandenen ohmschen Widerstand beschrieben, und der
wird bei Stromfluß ja auch heiß, weil Wirkleistung deponiert wird. |
 |
Wir werden aber noch folgendes lernen: Selbst absolut ideale
Dielelektrika haben in bestimmten Frequenzbereichen Imaginärteile ihrer DK! |
|
 |
In diesen Frequenzbereichen sind auch "ideale" Dielektrika (mit verschwindender
Gleichstromleitfähigkeit) verlustbehaftet – wir haben dielektrische Verluste;
das Dielektrikum wird heiß! |
|
 |
In diesen Frequenzbereichen werden dann auch ideale Dielektrika heiß –
hier steckt das Wirkprinzip der "Mikrowelle"! |
| | |
 |
Jetzt noch die schnellen Fragen: |
|
|
|
© H. Föll (MaWi für ET&IT - Script)