|
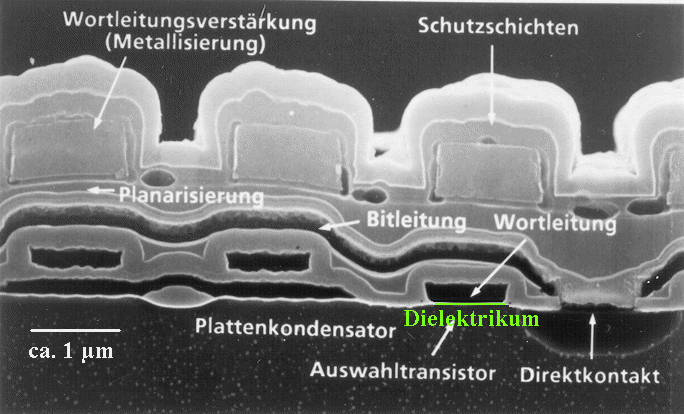
Im Bild unten sehen wir den Querschnitt durch eine Speicherzelle eines1 Mbit
Speichers (DRAM),
ca. Baujahr 1986. Heutzutage sieht das ganz
anders und ca. einen Faktor 5 kleiner aus; dummerweise kann man dann aber nicht mehr so leicht das Wesentliche sehen: |
|
 |
Das Dielektrikum (also ein Isolator; hier grün markiert) zwischen dem "Gate" des Transistors (mit "Wortleitung"
bezeichnet, also jedenfalls ein Leiter) und dem Si Substrat (ein Halbleiter, aber doch noch leitend), ist recht dünn.
Hier so um 10 nm; die Strichdicke oder selbst die weißen Partien im REM Bild) geben hier nicht die wirkliche
Dicke wieder). |
|
|
|
|
 |
Die Feldstärke
E in einer Schicht der Dicke d mit angelegter Spannung = Potentialdifferenz U
(man denke an den Plattenkondensator) ist bekanntlich E = U/d . |
|
 |
Wie groß ist denn so die Feldstärke in typischen Dielektrika des täglichen
Lebens und in unserem Chip? Was hält ein dielektrisches Material so aus? Es ist jetzt wichtig,
dass jeder und jede sich den ersten Teil der folgenden Übung anschaut und zumindest ein bißchen nachdenkt! |
| |
|
|
 |
Erraten! Die Feldstärken , die in Materialien
in einem Chip auftreten, sind viel
größer als im täglichen elektrotechnischen Leben! Und das, obwohl die Spannung, mit der ein Chip betrieben wird, nur ein paar Volt beträgt! |
 |
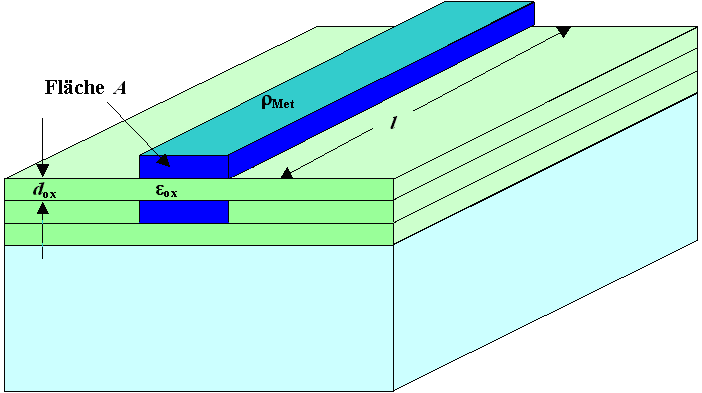
Für Strom und Stromdichte
gilt dasselbe. Die Graphik unten zeigt zwei typische Leiterbahnen
auf einem IC. Der in einer Leiterbahn fließende Strom liegt allenfalls im µA Bereich. Interessant
ist die Stromdichte, d. h. die A/cm2. |
|
 |
Es ist Zeit, auch darüber kurz nachzudenken! |
| |
|
 |
Wenden wir uns einer anderen Frage zu. Wir nehmen mal an, die untere Leiterbahn
im Bild oben liegt gerade auf Potential 0 V, d.h. auf Masse. In die obere Leiterbahn speisen wir ein Rechtecksignal
ein. Sagen wir + 3 V für 5 ns. Was kommt hinten raus? |
|
 |
Wem das nicht auf Anhieb klar ist möge bedenken, dass die beiden Leiterbahnen zusammen
einen parasitären Kondensator
darstellen, den wir zwar nicht wollen, aber trotzdem haben. Außerdem ist zwischen Eingang und Ausgang der ohmsche
Widerstand der Leiterbahn . |
|
 |
Das schreit nach einer Übung! |
|
|
|
| |
|
|
Warum Dielektrika wichtig sind |
| | |
 |
OK - der ET&IT Ingenieur weiß auch ohne Übung, dass wir eine Schaltung
der Art 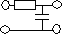 vorliegen haben, und dass die Zeitkonstante
t = RC die
Grenzfrequenz
fmax, d.h. die maximale Frequnz mit der Information übertragen werden kann, auf ungefähr
fmax » 1/t limitiert. vorliegen haben, und dass die Zeitkonstante
t = RC die
Grenzfrequenz
fmax, d.h. die maximale Frequnz mit der Information übertragen werden kann, auf ungefähr
fmax » 1/t limitiert. |
|
 |
In der Kapazität steckt die relative Dielektrizitätskonstante
er; für das in solchen Fällen übliche SiO2
gilt e r(SiO2) » 3.7. |
|
 |
Damit wissen wir auch, wie man die relative Dielektrizitätskonstante
(DK
) mißt: Steck das Zeug in einen Plattenkondensator mit Plattenfläche
A und Plattenabstand d. Seine Kapazität wird dann von C
0 = e0 · A/d auf Cmat
= e0 · er · A/d
ansteigen |
 |
Damit haben wir uns schon zwei hinreichend gute Gründe erarbeitet, warum
Dielektrika und Dielektrizitätskonstanten in der ET&IT wichtig sind. Es gibt aber noch viel mehr Gründe;
wir zählen mal die wichtigsten auf: |
|
 |
"Dielektrikum"
ist erstmal nur ein anderes Wort für Isolator.
Ohne Isolatoren keine ET&IT. Es sind aber nicht alle Isolatoren gleich - auf die Eigenschaften des Dielektrikums
kommt es schon an. IC Technik ist mindestens so viel "Dielektrikumstechnik" wie Halbleitertechnik. |
|
 |
Dielektrizitätskonstanten sind wichtig für alle Kondensatoren
– absichtliche oder unabsichtliche (= parasitäre). Die parasitären
Kapazitäten in ICs limitieren jetzt schon die Grenzfrequenzen.
Dielektrika mit kleineren Dielektrizitätskonstanten werden verzweifelt gesucht! |
|
 |
Die Grundstruktur des MOS Transistors beruht kritsch auf seinem "Gate" Dielektrikum.
Hier liegt der Schlüssel zu immer kleineren und schnelleren Transistoren! |
|
 |
Der Mikrowellenofen nutzt die dielektrischen Eigenschaften
des (relativ schlechten Isolators) "Wasser". |
|
 |
Piezoelektrische und ferroelektrische
Materialien, ohne die keine Elektronik (und kein modernes Autos) mehr auskommt, sind spezielle Dielektrika.. |
|
 |
Die gesamte Optik incl. der optischen Nachrichtenübertragung
über Glasfasern mit Lasern beruht auf dem Brechungsindex
n der optischen "Gläser
". Für n gilt aber die untenstehende extrem einfache Gleichung, die die "Optik" zurückführt
auf die dielektischen Eigenschaften des Materials |
|
|
|
 |
Wir sollten also mal überlegen, was wir über Dielektrika eigentlich
wissen möchten oder müssen. |
| |
|
© H. Föll (MaWi für ET&IT - Script)