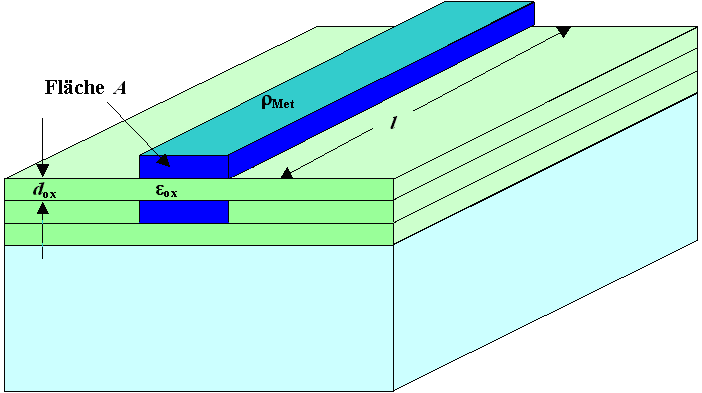
 |
Hier ist nochmals die in Kapitel 6.1.1
gezeigte Geometrie von Verbindungsleitungen in einer integrierten Schaltung |
| |
|
| | | |
|
1
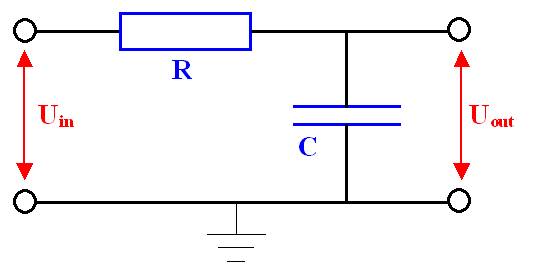
Zeige, dass damit folgendes Ersatzschaltbild gilt und berechne mit dem gegebenen Werten sowohl den Widerstand R
als auch die Kapazität C. |
|
 |
Für den spezifischen Widerstand der Leiterbahn kann der Wert r = 2 µWcm verwendet; für dOx, die Länge l und die Fläche
A nehmen wir realistische Werte von 300 nm, 1 mm bzw. 0,1 µm 2; für
die relative Dielektrizitätskonstante des Dielektrikums zwischen den Leiterbahnen gilt eox
= 4. |
| |
|
|
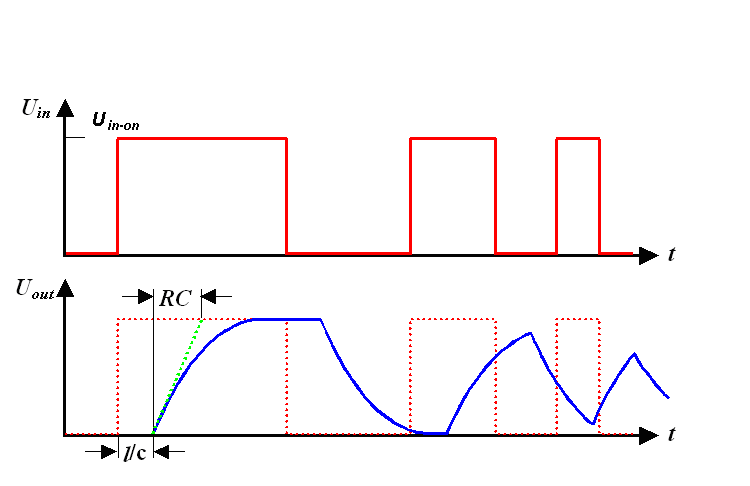
2. Zeige, dass sich bei Einspeisung eines Rechtecksignals am Eingang der
Signalverlauf am Ausgang wie unten gezeigt ergibt. |
|
|
|
|
|
Hinweis: Die folgendeDifferentialgleichung gilt es zu lösen (Warum?) |
| |
| I = C · |
dUout
dt |
= |
Uin – Uout
R |
|
|
|
|
Lösungen für die Fälle: Spannung "rauf" oder Spannung "runter" sind
(Warum?): |
| |
|
Uout = Uin-on · {1 – exp– (t/RC)} |
|
Uout = Uin-on · exp– (t/RC)} |
|
|
|
3. Diskutiere:
- Die Bedeutung der Zeitkonstanten t = RC für die maximale Taktfrequenz von integrierten Schaltungen.
- Die mögliche Beziehung der errechneten Zeitkonstante des Beispiels zu derzeitigen Taktfrequenzen realer Chips.
- Mögliche Maßnahmen zur Verringerung dieser Zeitkonstanten unter Berücksichtigung der Eigenschaften realer Materialien.
|
|
| |
 |
Lösung |
| |
© H. Föll (MaWi für ET&IT - Script)
6.1.1 Feldstaerke, Stromdichte und Zeitkonstanten 
Mit Frame