|
Die obige Frage hat eine einfache Antwort: Sorge dafür, dass das Dielektrikum
einem elektrischen Feld ausgesetzt ist, das so aussieht: |
| |
| E | = |
E0 · cos(wt) |
| | | | | | | oder eleganter: |
| | | | | E | = |
E0 · exp(iw t) |
|
|
|
 |
Wir nehmen natürlich für was jetzt folgt gleich die viel bequemere komplexe
Schreibweise. |
 |
Wie macht man das experimentell? Je nun - da wir bis zu sehr hohen Frequenzen (z. B. 1016
Hz) gehen wollen, hängt das experimentelle Vorgehen vom Frequenzbereich ab. Hier sind ein paar Vorschläge: |
| |
|
|
 |
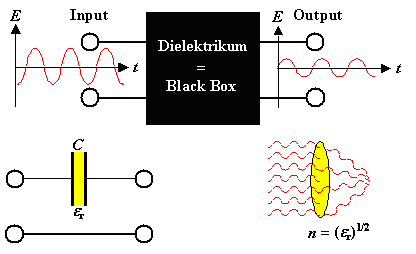
Was wir tun kann man einfach beschreiben: Unser Dielektrikum ist ein schwarzer Kasten, eine
"Black box" ; wir haben erstmal keine Ahnung was drin ist. Wir können aber einen "Eingang" = Input
definieren in dem das Wechselfeld eingespeist wird, und einen Ausgang oder "Output" wo es - verändert - wieder
rauskommt. |
|
 |
Solange der schwarze Kasten "linear" ist (und das ist jeder schwarze Kasten für nicht zu
große Amplituden), diktiert die Logik, dass am Ausgang nur zwei Dinge geschehen
können:
- Die Amplitude hat sich geändert, d.h. aus E0 = Ein wird Eout.
- Die Phase hat sich geändert, sie ist um irgendeinen Wert f verschoben
|
|
 |
In anderen Worten: Das Eingangssignal sieht so aus: Ein = Ei
· exp(iw
t); am Ausgang haben wir: Eout = Eu · exp[i(wt
+ f)]. |
|
 |
Das kann man aber auch so darstellen: |
| |
| Eout | = |
f(w) · Ein | = |
e(w ) · exp{if(w)} ·
Ein |
|
|
|
 |
Die Größe f(w) kann ganz generell als eine komplexe Zahl eexp(if) für eine gegebene Frequenz w
dargestellt werden, oder allgemeiner und wie gezeigt als eine komplexe Funktion der
Frequenz. Diese komplexe Funktion enthält offenbar die gesamte Information über die black box, und damit alles was man über das Dielektrikum wissen muss. |
 |
Wir kennen diese komplexe Funktion schon; es ist nichts anderes als die dielektrische Funktion
e(w) des Materials (wobei wir uns um gewisse Feinheiten der
Definition hier keine Gedanken machen). Außerdem schreiben wir die dielektrische Funktion in der Regel nicht in der
"Zeigerform" sondern sortiert nach Real- und Imaginärteil. Wie das geht is klar, sonst Link
betätigen. |
|
 |
Wir haben zwar bei der Einführung der dielektrischen Funktion die Eingangsspannung
oder Feldstärke mit dem Ausgangsstrom bzw. der Stromdichte verknüpft, aber
man braucht den Ausgangsstorm nur per Lastwiderstand in Spannung umwandeln, und schon haben wir die Verküpfung zwischen
Eingang und Ausgang wie hier gewünscht. |
 |
Die alte Definition des Brechungsindexs n2 = er
übertragen wir auf die komplexe dielektrische Funktion, wir bekommen dann einen komplexen Brechungsindex n* definiert als
|
| |
|
|
 |
Aus historischen Gründen nennt man den Realteil n (ohne Strich "'")
und den Imaginärteil k. Damit haben wir: |
|
|
| n*2(w) | = |
e(w) | = |
e'(w) – ie''(w) |
| n2 | = | 1
2 |
æ
ç
è | æ
è
|
e' 2 + e'' 2 |
ö
ø | ½ |
+ e ' | ö
÷
ø
|
| k2 | = | 1
2 |
æ
ç
è | æ
è
| e ' 2 + e'' 2 |
ö
ø | ½ |
– e' | ö
÷
ø
|
|
|
 |
Die gute Nachricht ist: Diese Formeln muss man nicht wissen; die Grundformel n
2 = e aber schon. |
 |
Damit ist die dielektrische Funktion eine ungeheure mächtige Materialgröße.
Sie wird besonders bei hohen Frequenzen (GHz bis optisch) wichtig und spannend. Es bleibt nur noch, die dielektrische
Funktion eines Materials zu berechnen. Dazu gibt es zwei gute und eine schlechte Nachricht |
|  |
Gute Nachricht 1: Es gibt nur zwei grundlegende Mechanismen,
die wir berücksichtigen müssen: Resonanz und Relaxation. |
|
 |
Schlechte Nachricht: Die zugehörige Mathematik ist nicht so ganz einfach und führt zu länglichen Formeln.
|
|
 |
Gute Nachricht 2: Haben wir aber in der Physik schon mal gehabt und - wir lassen die Mathe hier
weitgehend weg! |
| | |
 |
Damit zu den schnellen Fragen: |
|
|
|
| | |
© H. Föll (MaWi für ET&IT - Script)