|
Das Gitter |
| |
|
 |
Die "regelmäßige Anordnung"
läßt sich mathematisch durch ein Raumgitter erzeugen. |
| |
 |
 |
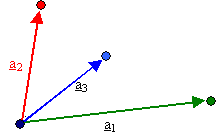
Vier Punkte im Raum; einer davon der Ursprung.
Drei
Basisvektoren
ai
führen zu den drei anderen Punkten |
Fortsetzung der Raumpunkte;
an sich klar, aber ziemlich
unübersichtlich |
|
 |
Wie man sieht, sind Zeichnungen von mathematischen Punkten (= ¥
klein), die gleichmäßig im Raum verteilt sind (von – ¥ bis +
¥ ) - unmöglich, und
- selbst mit Einschränkungen noch recht unübersichtlich.
|
|
 |
Mit Hilfslinien oder "Gitterlinien" und Kreisen
statt Punkten wird's besser: |
|
|
 |
Deutlich besser.
Große Gitter"punkte"
und Gitterlinien als Hilfslinien |
|
 |
Noch besser ist eine formale Definition: Ein (periodisches) Raumgitter ist definiert
durch: - Einem Vektortripel, bestehend aus den Basisvektoren
a 1, a2, a3, mit denen man ein Parallelepiped
aufspannen kann, das wir Elementarzelle (oder manchmal auch Einheitszelle)
nennen.
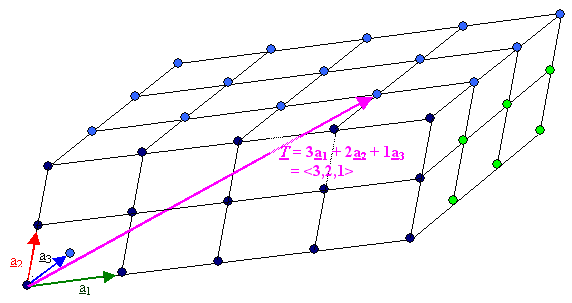
- Einem Satz von ¥ vielen Translationsvektoren
T dieses Gitters, die durch T = ua1
+ va2 + wa3 (mit (u, v, w) = alle ganzen
Zahlen) definiert werden, und deren Endpunkte die Punkte des Gitters repräsentieren.
|
|
 |
Damit ist ein beliebiges
Raumgitter eindeutig definiert. |
|
| |
 |
Was sind die "identischen Bausteine",
die wir die Basis des Kristalls nennen? |
|
 |
In einfachsten Fall besteht die Basis nur aus einem
einzigen Atom oder mindesten 2 Ionen (warum?). Wenn
wir auf jeden Gitterpunkt dann ein einziges solches "Kügelchen" setzen oder eine "Hantel" aus zwei
Kugeln, bekommen wir die Kristallbildchen, die in Kapitel. 2.1.4
schon mal gezeigt wurden. |
 |
Wir halten als Definition eines Kristall also fest: |
| |
| Kristall |
= |
Gitter |
+ |
Basis |
 |
= |
 |
+ |
 |
 |
= |
 |
+ |
 |
| Die Gitterpunkte
sind hier die kleinen roten Punkte (auch ganz links!) |
|
|
 |
Die beiden zweidimensionalen
Beispiele zeigen:
- Eine klare dichteste
Kugelpackung mit einem Atom in der Basis. Das Gitter ist offenbar hexagonal.
- Einen möglichen Ionenkristall. Das Gitter ist offenbar kubisch.
Die Basis besteht aus zwei (verschieden) geladenen Ionen.
|
|
 |
Mit den Begriffen kubisch
und hexagonal haben wir übrigens ganz bestimmte (und unmittelbar völlig
klare) Symmetrien beschrieben, die diese beiden speziellen Gitter haben. |
 |
Ein unangenehmer Verdacht kommt hoch. Kann es sein, dass die Kombination eines
Gitter plus einer möglicherweise komplizierten Basis in drei Dimensionen eine Unzahl
von Kristallen - von einfachen kubischen Strukturen bis zu hochkomplexen Gebilden - produzieren kann? |
|
 |
Ja! Gottseidank - die Welt wäre sonst erheblich langweiliger! Wer Lust hat
schaut sich mal die Bildchen einiger noch relativ einfacher
Kristalle an, oder gleich die Edelsteine. Bemerkenswert
ist beispielsweise der Opal. |
|
| |
 |
Wir machen uns das Leben hier aber einfach und schauen uns nur einen kleinen,
aber wichtigen Ausschnitt aus der Welt der Kristalle etwas genauer an. Das tun wir,
indem wir die Oberklasse "allgemein definiertes Gitter" in Unterklassen einteilen, so wie man die Oberklasse "Lebewesen"
ja auch unterteilt in z. B. Tiere, Pflanzen, Schleimpilze und Banker. Wir unterteilen "Gitter" in 14 Untergruppen,
genannt "Bravais-Gitter". Insgesamt gibt es aber nur 7 grundlegend
verschiedenen Gitter-Symmetrien; diese Symmetrieklassen werden (verallgemeinernd) Kristallsysteme genannt (und nicht
"Gittersysteme", wie eigentlich zu erwarten). Der Link führt zum vollen
Programm; hier schauen wir nur auf wenige wichtige Punkte: |
|
 |
Erstens betrachten wir hier nur 2 Kristallsysteme mit hoher
Symmetrie, nämlich das kubische und das hexagonale.
Zum kubischen Kristallsystem gehören drei Bravais-Gitter, zum hexagonalen nur eins: |
| |
|
 |
Die gezeigten Gitter haben einen hohen Grad an Symmetrie
- im Gegensatz zu dem allgemeinen Gitter, bei dem alle drei Basisvektoren verschieden lang sind und die drei Winkel zwischen
den Basisvektoren beliebige Werte haben können. |
|
 |
Die kubischen Gitter haben beispielsweise 4-fache Rotationssysmmetrie
um drei Achsen, Spiegelsymmetrie an drei Ebenen (Bild und Spiegelbild sind identisch) und Inversionssymmetrie (Vertauschen
von r mit –r bringt nichts Neues). |
|
 |
In den drei kubischen Gittern haben alle drei Basisvektoren dieselbe Länge;
beim hexagonalen Gitter ist die Länge von a3 = c im Prinzip zwar frei, aber spätestens dann
eindeutig gegeben, wenn wir das Gitter für einen dichtest gepackten
Kristall verwenden. Man bezeichnet dann die jeweilige Länge der relevanten Basisvektoren als
Gitterkonstante a. |
 |
Zweitens beschränken wir uns auf eine
Basis mit nur 1-2 Atomen / Ionen. |
 |
Damit können wir folgende, weitreichende Aussagen machen: |
| |
- Die Kombination von 1 Atom in der Basis mit dem kubisch-flächenzentrierten oder fcc-Gitter (face centered cubic) ergibt immer eine dichteste Kugelpackung.
Etwa 30 % der Elemente kristallieren in einem solchen fcc
-Gitter oder -Kristall (hier ist der Unterschied
bedeutungslos), z.B. Al, Ni, Cu, Pd, Ag, Pt, Au sowie alle Edelgase.
- Die Kombination von 2
identischen Atomen in der Basis (eines bei (0,0,0), das andere
bei (S,S,½) mit dem hexagonalen Gitter ergibt ebenfalls eine
dichteste Kugelpackung.
Etwa 35 % aller Elemente kristallisieren in
einem solchen hcp-Kristall (hexagonal close packed), darunter beispielsweise
Mg, Re, Co, Zn, Cd, C (als Graphit), aber auch z.B. N bei tiefer Temperatur.
- Die Kombination von 1 Atom in der Basis mit dem kubisch-raumzentrierten oder bcc-Gitter (body
centered cubic) ergibt keine dichteste Kugelpackung.
Etwa 30 % der
Elemente kristallieren in dieser Form, z. B. K, Rb, Cs, V, Nb, Ta, Cr,
Mo und W.
- Die Kombination von 2 Atomen in der Basis (bei (0,0,0) und (¼, ¼,
¼) ) mit dem kubisch-flächenzentrierten oder fcc-Gitter (face centered cubic)
ergibt keine dichteste Kugelpackung, dafür aber die Grundstruktur der meisten Halbleiter wie Si, Ge (Diamantstruktur), GaAs, InP,
... (Zinkblendestruktur).
|
|
 |
Diese 4 Punkte werden hier absichtlich nicht illustriert, denn dafür gibt es eine
Übung! |
| |
|
| |
|
© H. Föll (MaWi für ET&IT - Script)